Maple – это мощная система для символических и численных вычислений, позволяющая решать математические задачи любой сложности. Но чтобы в полной мере воспользоваться её возможностями, важно понимать, как правильно организовать процесс вычислений. В этой статье мы подробно рассмотрим, как шаг за шагом посчитать выражение в Maple, избегая распространённых ошибок и упрощая расчёты.
Для начала важно правильно определить выражение в Maple. Ввод переменных и функций происходит в привычной математической нотации, но с учётом синтаксиса Maple. Например, чтобы задать квадратичное выражение y = x^2 + 3x + 2, достаточно написать:
y := x^2 + 3*x + 2;
После ввода выражения можно приступать к поэтапным вычислениям. Maple позволяет легко дифференцировать, интегрировать, раскрывать скобки, упрощать выражения и подставлять значения в переменные. Ключевые команды, такие как diff, int, expand, simplify и subs, открывают доступ к этим операциям. Важно понимать, как именно они работают и в какой последовательности их применять.
Мы разберём, как пошагово производить вычисления, контролировать результат на каждом этапе и исправлять ошибки при их возникновении. Это позволит максимально эффективно использовать Maple при решении задач по математике, физике или инженерным дисциплинам.
Установка Maple и подготовка среды для вычислений
Для начала работы с Maple необходимо загрузить установочный файл с официального сайта разработчика. Версия должна соответствовать операционной системе: Windows, macOS или Linux. После скачивания запустите установщик и следуйте инструкциям мастера установки. Выберите директорию для установки, при необходимости укажите лицензионный ключ.
После завершения установки откройте Maple. При первом запуске программа предложит настроить рабочую среду. Рекомендуется выбрать стандартный интерфейс с поддержкой математического ввода и многостраничного режима. Это обеспечит удобное выполнение вычислений и управление документами.
Для удобства работы настройте следующие параметры в разделе «Параметры» → «Настройки среды»:
1. Установите удобный шрифт и его размер для отображения математических формул и текста. Это повысит читаемость вычислений.
2. Активируйте автосохранение проектов с интервалом 5–10 минут, чтобы избежать потери данных при сбоях.
3. Включите автоматическое завершение ввода команд. Это ускорит написание кода и снизит количество опечаток.
Для Linux требуется дополнительная настройка переменных окружения. После установки выполните в терминале команду source /opt/maple/bin/maplevars.sh, чтобы настроить пути к библиотекам.
Проверить успешность установки можно, запустив команду restart: в рабочем окне Maple. Если ошибок нет, среда готова к выполнению вычислений.
Ввод математических выражений в Maple
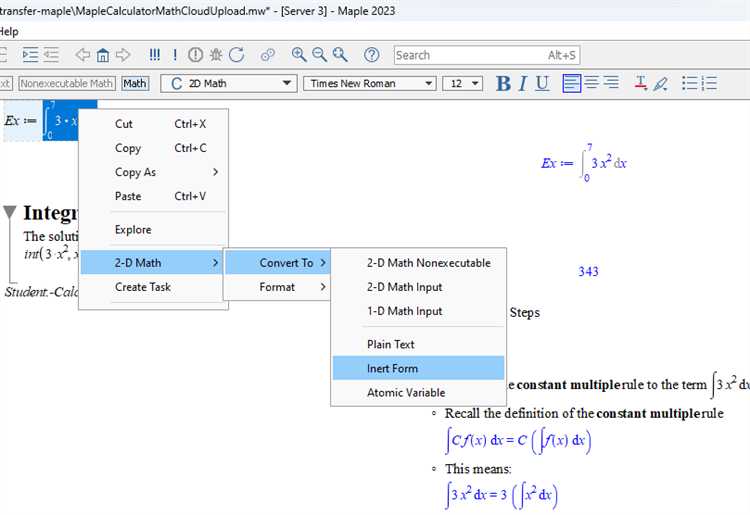
Для корректного ввода математических выражений в Maple необходимо учитывать синтаксис и особенности программы. Maple поддерживает стандартные математические операции, функции и специальные символы.
- Арифметические операции: сложение (+), вычитание (-), умножение (*), деление (/), возведение в степень (^). Например:
2 * x + 3^2. - Скобки для приоритетов: использование круглых скобок меняет порядок вычислений. Пример:
(2 + 3) * 4отличается от2 + 3 * 4. - Десятичные числа: вводятся через точку:
3.14, а не через запятую. - Функции: стандартные функции, такие как
sin(x),cos(x),exp(x),ln(x). Аргументы функций заключаются в круглые скобки. - Многочлены и дроби: Maple распознает многочлены, введенные в виде суммы или разности членов. Для дробей используйте прямой слэш:
(x^2 + 3*x + 2)/(x + 1). - Матричные выражения: создаются с помощью
Matrix(). Например,Matrix(2, 2, [[1, 2], [3, 4]])создаст матрицу 2×2. - Комплексные числа: вводятся как
3 + 4*I, гдеI– мнимая единица. - Дифференцирование и интегрирование: команды
diff(f, x)иint(f, x)позволяют вычислять производные и интегралы. Например:diff(x^3, x)вернет3*x^2. - Суммы и произведения: для ввода сумм используйте
sum(expression, variable = range), например:sum(k^2, k = 1..5). Для произведений –product(expression, variable = range). - Логические выражения: Maple поддерживает
and,or,not, а также условия=, <, >, <=, >=, <>.
Для проверки правильности ввода выражения в Maple рекомендуется использовать команду evalf(), чтобы увидеть численное значение, или simplify() для упрощения.
Применение стандартных операторов и функций
Maple поддерживает стандартные арифметические операторы: +, -, *, / и ^. Эти операторы используются для сложения, вычитания, умножения, деления и возведения в степень. Например, выражение 3 * (2 + 5)^2 в Maple записывается так же, как и в математике: 3*(2 + 5)^2;. После ввода команда Enter вычисляет результат.
Для работы с выражениями Maple предоставляет стандартные функции, такие как sqrt(x) – квадратный корень, exp(x) – экспонента, ln(x) – натуральный логарифм, sin(x), cos(x), tan(x) – тригонометрические функции. Например, результат выражения sqrt(16) вычисляется как 4, а ln(exp(1)) даст 1.
Функции в Maple поддерживают вложенность. Например, sin(ln(2)) + cos(exp(1)) вычисляется напрямую. Если необходимо упростить результат, используется команда simplify(). Например, выражение simplify(sin(Pi/4) + cos(Pi/4)) вернёт sqrt(2).
Для численного вычисления используется функция evalf(). Пример: evalf(Pi) возвращает значение числа π с высокой точностью. Можно задать требуемое количество знаков: evalf(Pi, 10) вернёт 3.1415926536.
Чтобы вычислить производные и интегралы, Maple использует diff() и int(). Например, производная x^2 + 3*x по x находится как diff(x^2 + 3*x, x);, результат – 2*x + 3. Для интегрирования применяется int(x^2, x);, и результат будет x^3/3.
Maple позволяет сохранять результаты в переменные. Например, result := sqrt(25); сохраняет значение 5 в переменную result. Это упрощает доступ к промежуточным вычислениям в дальнейших выражениях.
Понимание использования операторов и функций Maple позволяет эффективно решать математические задачи, упрощать выражения и получать численные результаты с высокой точностью.
Распознавание синтаксических ошибок и их исправление
1. Незакрытые скобки: Maple чувствителен к правильному балансу скобок. Если выражение содержит незакрытые или неправильно вложенные скобки, Maple выдаст ошибку «unexpected end of expression». Для исправления необходимо проверить все открывающиеся и закрывающиеся скобки, включая (), [] и {}. Использование команды prettyprint() помогает визуализировать вложенность скобок.
2. Отсутствие точки с запятой или двоеточия: В конце каждой команды в Maple требуется ; или :. Пропуск этой конструкции приводит к ошибке. В таких случаях Maple выдает сообщение «missing ; or : at end of statement». Для исправления достаточно добавить пропущенный символ в конце строки.
3. Неправильное именование переменных: В Maple переменные не должны начинаться с цифры и содержать пробелы. Например, 2variable вызовет ошибку. Для устранения проблемы следует переименовать переменную, например, на variable2.
4. Использование неинициализированных переменных: Обращение к переменной, значение которой не было задано, приводит к ошибке «unknown variable». Для исправления требуется убедиться, что переменная проинициализирована корректно перед использованием.
5. Ошибки в вызове функций: Неправильное количество аргументов или пропуск обязательных параметров при вызове функций вызывает ошибки. Например, solve(x^2 + 4) без указания переменной не выполнится. Правильный вызов: solve(x^2 + 4, x).
6. Конфликт имен пользовательских и системных функций: Maple имеет встроенные функции с определенными именами. Если пользователь создаст переменную с таким же именем, это приведет к конфликту. Например, если присвоить sin := 5, то вызов sin(x) завершится ошибкой. Для устранения конфликта рекомендуется избегать использования зарезервированных имен или воспользоваться командой unassign(‘имя’).
Эффективное исправление синтаксических ошибок в Maple требует внимательности и понимания структуры кода. Визуализация, тщательная проверка и использование отладочных инструментов значительно ускоряют этот процесс.
Пошаговое выполнение вычислений в Maple
В Maple можно выполнить поэтапные вычисления, чтобы лучше понять процесс упрощения или преобразования выражений. Для этого используются команды, позволяющие по шагам анализировать каждый этап решения.
- evalb: Проверяет истинность выражения. Например,
evalb(2 + 2 = 4);вернётtrue. - eval: Выполняет вычисление выражения. Последовательное применение
evalпозволяет по шагам видеть изменения. Пример:expr := (x + 2)^2;eval(expr);→(x + 2)^2expand(%);→x^2 + 4x + 4
- subs: Подставляет значения в выражение. Например:
subs(x = 3, x^2 + 2*x);→15
- simplify: Упрощает выражение:
simplify(sin(x)^2 + cos(x)^2);→1
- expand: Раскрывает скобки:
expand((x + 1)^3);→x^3 + 3x^2 + 3x + 1
- collect: Сортирует выражение по степеням переменной:
collect(x^2 + 2*x + x^2, x);→2*x^2 + 2*x
Для поэтапного выполнения можно последовательно применять команды:
- Записываем выражение:
expr := (x + 2)^2 + 2*x; - Выполняем развёртывание скобок:
expand(expr); - Подставляем значение переменной:
subs(x = 1, %); - Упрощаем результат:
simplify(%);
Такой подход позволяет контролировать каждый этап, анализировать ошибки и корректировать вычисления по мере необходимости.
Использование команд упрощения и преобразования выражений
В Maple для пошагового анализа выражений важны команды, которые изменяют форму выражения без потери смысла. Ключевая команда – simplify, которая автоматически применяет набор преобразований: сокращение дробей, раскрытие скобок, объединение подобных членов. Для точечного контроля используют параметры, например, simplify(expr, symbolic) – упрощение с использованием символических правил.
Для разложения выражения на множители применяется factor. Она эффективна для полиномов и рациональных функций. Результат удобен для последующего интегрирования или решения уравнений. Если нужно разложить выражение по конкретному виду, можно использовать factor(expr, 'x'), что ограничит факторизацию переменной x.
Команда expand раскрывает скобки и возводит в степень многочлены. Она полезна, когда требуется получить развернутое выражение для дальнейших вычислений или интегралов. Важно применять expand после factor, если нужно вернуться к полному виду, но с учётом уже упрощённых частей.
Для замены переменных или частей выражения используют subs, что позволяет пошагово менять компоненты без ручного редактирования. Команда combine обратна expand и применяется для объединения логарифмов, тригонометрических функций и степеней с одинаковыми основаниями, что упрощает структуру выражения.
Рекомендуется комбинировать эти команды в последовательности: сначала expand для раскрытия, затем simplify с параметрами для уменьшения сложности, затем factor для выделения множителей и combine для сжатия выражений. Это позволяет получить оптимальный вид с подробной структурой для анализа или последующего вычисления.
Решение уравнений и систем уравнений в Maple

В Maple для решения уравнений применяется команда solve. Чтобы найти корни уравнения f(x) = 0, используйте синтаксис:
solve(f(x), x);
Для систем уравнений передайте список или множество уравнений и список переменных:
solve({eq1, eq2, ..., eqn}, {x, y, ..., z});
Maple по умолчанию ищет точные алгебраические решения. Для численных приближений используйте fsolve:
fsolve(f(x), x, a..b); – ограничивает поиск корней интервалом [a, b].
При работе с системами нелинейных уравнений fsolve также применим, возвращая численные решения:
fsolve({eq1, eq2}, {x, y});
Для уравнений с параметрами желательно явно задавать переменные и параметры, чтобы избежать неоднозначностей.
Если уравнение содержит сложные функции (тригонометрические, экспоненты и др.), результат solve может быть выражен через корни и функции типа RootOf. Для упрощения используйте simplify или переходите к численным методам.
Для поиска всех комплексных корней добавьте опцию complex в fsolve:
fsolve(f(x), x, complex);
В случае неоднозначности решений рекомендуется исследовать уравнение аналитически или разбивать его на частные случаи.
Визуализация результатов вычислений в графическом виде
Для построения графиков в Maple используется команда plot(). Она позволяет визуализировать функции, уравнения и числовые данные с точной настройкой осей, диапазонов и стиля отображения. Например, чтобы построить график функции f := x -> sin(x)/x на интервале от -10 до 10, применяется команда:
plot(f(x), x = -10..10);
Maple поддерживает одновременное отображение нескольких функций с помощью списков:
plot([sin(x), cos(x)], x = 0..2*Pi);
Для анализа поведения решений дифференциальных уравнений удобно использовать plot с параметром parametric для параметрических кривых. Пример:
plot([cos(t), sin(t), t = 0..2*Pi]);
Чтобы детализировать график, можно менять количество точек дискретизации через опцию numpoints, например:
plot(f(x), x = -10..10, numpoints = 500);
Maple позволяет строить графики не только функций, но и точечных данных. Для этого используется команда pointplot из пакета plots:
with(plots):
pointplot([[1,2], [2,3], [3,5]], symbol = circle, symbolsize = 10);
Визуализация 3D-графиков реализуется через plot3d. Например, поверхность z = x^2 + y^2 на квадрате [-2,2]x[-2,2]:
plot3d(x^2 + y^2, x = -2..2, y = -2..2);
Для интерактивного исследования графиков удобно использовать встроенный интерфейс, позволяющий масштабировать и вращать 3D-объекты мышью.
plot(f(x), x = 0..10, title = "График функции f(x)", labels = ["x", "f(x)"], legend = ["f(x)"]);
Вопрос-ответ:
Как в Maple организовать пошаговое вычисление сложного выражения?
В Maple для выполнения пошагового вычисления удобно использовать команды, которые позволяют раскрывать и упрощать выражение по частям. Например, можно применять функцию simplify или expand последовательно, отслеживая каждый этап. Также полезно разбивать выражение на составляющие и вычислять их отдельно, выводя промежуточные результаты. В интерфейсе Maple можно включить вывод каждого шага, чтобы видеть, как именно меняется выражение в процессе.
Можно ли в Maple автоматизировать вывод промежуточных вычислений для учебных целей?
Да, Maple поддерживает возможность показать промежуточные шаги с помощью специальных пакетов или встроенных функций. Например, можно использовать пакеты, предназначенные для математического анализа или алгебры, которые автоматически выводят отдельные этапы преобразований. Кроме того, для обучения часто применяют команды с параметрами, которые выводят подробные результаты, что помогает лучше понять логику преобразований.
Как контролировать порядок выполнения операций при расчёте выражения в Maple?
В Maple вычисления следуют стандартным правилам приоритета операций, но если нужно изменить порядок, можно использовать скобки, чтобы явно задать последовательность действий. Также есть возможность писать отдельные команды для каждого этапа, фиксируя промежуточные результаты в переменных. Такой подход позволяет точно управлять тем, что и когда считается, и избежать нежелательных упрощений.
Какие инструменты Maple помогают понять, как упростить выражение пошагово?
Maple содержит несколько функций для пошагового упрощения, например, simplify, factor, expand и collect. Каждый из этих инструментов фокусируется на определённом виде преобразований: simplify облегчает выражение, factor выделяет множители, expand раскрывает скобки, а collect группирует похожие члены. Используя их поочерёдно и внимательно отслеживая изменения, можно увидеть, как преобразуется выражение на каждом этапе.