Как построить эллипс в mathcad

Эллипс в Mathcad можно задать параметрически с использованием стандартных функций cos и sin. Основные параметры – длины полуосей a и b, а также диапазон значений параметра t, задающего угол в радианах. Типичная запись: x(t) := a·cos(t), y(t) := b·sin(t), где t изменяется от 0 до 2π.

Для построения графика необходимо задать вектор значений t с шагом, обеспечивающим плавность кривой, например: t := 0, 0.01 .. 2·π. Далее формируются векторы координат: x := a·cos(t), y := b·sin(t). Построение выполняется через оператор 2D-графика, где в качестве аргумента по оси X задаётся x, а по оси Y – y.

При необходимости эллипс можно повернуть на угол φ с помощью поворотной матрицы. Координаты преобразуются следующим образом: x′ := x·cos(φ) − y·sin(φ), y′ := x·sin(φ) + y·cos(φ). Это особенно полезно при моделировании наклонных сечений или анализа траекторий.

Для удобства повторного использования рекомендуется оформить построение эллипса в виде функции с параметрами: a, b, φ и шагом дискретизации. Такой подход позволяет быстро изменять форму и ориентацию эллипса без правки основных выражений.

Определение параметров эллипса: полуоси и центр

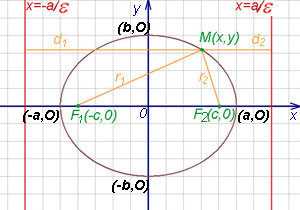
Для построения эллипса в Mathcad необходимо задать его основные параметры: длину полуосей и координаты центра. Без этого невозможно корректное математическое описание фигуры.

• Полуось a – длина вдоль оси X. Значение a должно быть положительным числом, определяющим «ширину» эллипса.
• Полуось b – длина вдоль оси Y. Значение b также задаётся положительным числом и отвечает за «высоту» эллипса.
• Центр эллипса – координаты (x₀, y₀). Они определяют положение эллипса на плоскости и задаются через переменные, например:
  • x₀ := 0
  • y₀ := 0

Рекомендуется вводить параметры через отдельные переменные, чтобы обеспечить гибкость при последующих изменениях и построениях.

1. Задайте значения полуосей, например: a := 5, b := 3.
2. Определите координаты центра: x₀ := 2, y₀ := -1.
3. Убедитесь, что все переменные отображаются в рабочей области без ошибок – это важно для корректного построения графика.

Эти параметры будут использоваться при параметрическом задании координат точек эллипса. Без их точного указания построение фигуры невозможно.

Создание уравнения эллипса в декартовых координатах

Для построения эллипса в Mathcad необходимо задать его уравнение в декартовой системе координат. Стандартная форма уравнения эллипса с центром в начале координат:

x²/a² + y²/b² = 1

Параметры a и b обозначают длины полуосей эллипса. Если a > b, эллипс вытянут вдоль оси x, если b > a – вдоль оси y.

В Mathcad рекомендуется использовать параметрическое представление, однако уравнение в явной форме удобно для анализа и построения через функции. Чтобы выразить y через x, преобразуйте исходное уравнение:

y(x) := ±b·√(1 — (x²/a²))

В Mathcad используйте определение функции с учётом области допустимых значений: abs(x) ≤ a. Например:

y₁(x) := b·sqrt(1 — (x²/a²))

y₂(x) := -b·sqrt(1 — (x²/a²))

Для построения графика задайте диапазон x := -a, -a+Δx .. a, где Δx – шаг дискретизации. Используйте plot или XY-Plot для отображения двух функций y₁(x) и y₂(x).

Если центр эллипса смещён, используйте уравнение:

((x — x₀)²/a²) + ((y — y₀)²/b²) = 1

В этом случае замените x на x — x₀ и y на y — y₀ в определении функций, а диапазон x сдвиньте на x₀.

Задание диапазона переменной для построения графика

Для построения эллипса в Mathcad необходимо задать параметрическую переменную, по которой будут рассчитываться координаты точек. Как правило, используется переменная t, отвечающая за параметр угла в радианах.

Рекомендуемый диапазон: t := 0, 0.01..2·π. Шаг 0.01 обеспечивает достаточную точность при отрисовке кривой без перегрузки системы.

Диапазон задаётся с помощью троеточечной записи: начальное значение, шаг, конечное значение. Символ π вводится с клавиатуры как Ctrl + Shift + P.

Пример корректного задания диапазона:

t := 0, 0.01..2·π

После определения диапазона переменной можно перейти к вычислению координат точек эллипса по формулам:

x(t) := a·cos(t)
y(t) := b·sin(t)

Построение графика выполняется функцией plot с подстановкой диапазона переменной t:

plot(x(t), y(t))

Для построения эллипса в Mathcad используются параметрические уравнения: x(t) = a·cos(t) и y(t) = b·sin(t), где a и b – полуоси, t – параметр, изменяющийся в диапазоне от 0 до 2π. Задайте этот диапазон с шагом, например, 0.01: t := 0, 0.01..2·π.

Полуоси определяются конкретными значениями: a := 5, b := 3. Затем вычисляются координаты: x(t) и y(t).

Функция plot вызывается через графическое окно вставки 2D-графика. Перетащите его на рабочую область, щелкните по оси X и введите x(t), затем по оси Y – y(t).

Если Mathcad не распознаёт переменную t как векторную, убедитесь, что диапазон t определён корректно. При необходимости примените команду vectorize для выражений x(t) и y(t).

Чтобы эллипс отображался корректно, отключите автоматическое масштабирование и вручную задайте равные интервалы по осям X и Y. Это обеспечит правильные пропорции фигуры.

Для повышения наглядности используйте параметры форматирования: измените цвет линии, увеличьте её толщину, добавьте сетку и подписи осей. Эти настройки доступны через двойной щелчок по области графика.

Преобразование уравнения эллипса в параметрическую форму

Стандартное каноническое уравнение эллипса имеет вид: \( \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \), где \( a \) – длина полуоси по оси X, \( b \) – длина полуоси по оси Y.

Для построения эллипса в Mathcad необходимо использовать параметрическую форму, где координаты точки определяются через параметр \( t \), изменяющийся на интервале от \( 0 \) до \( 2\pi \). Параметризация позволяет избежать проблемы множественных значений \( y \) при одном \( x \) и упростить построение графика.

Параметрическое уравнение эллипса задаётся следующим образом:

\( x(t) := a \cdot \cos(t) \)

\( y(t) := b \cdot \sin(t) \)

Перед построением необходимо определить диапазон параметра:

\( t := 0, \Delta t .. 2 \cdot \pi \), где \( \Delta t \) – шаг дискретизации, например, \( 0{,}1 \)

Для корректного отображения эллипса в Mathcad необходимо убедиться, что переменные \( a \) и \( b \) заданы заранее, например:

\( a := 5 \)

\( b := 3 \)

Если эллипс смещён относительно начала координат, добавьте смещения \( x_0 \) и \( y_0 \) в уравнение:

\( x(t) := x_0 + a \cdot \cos(t) \)

\( y(t) := y_0 + b \cdot \sin(t) \)

Это позволит задать эллипс с произвольным центром. Например, \( x_0 := 2 \), \( y_0 := -1 \) – центр эллипса будет в точке (2, −1).

Построение эллипса с помощью параметрических уравнений

Для построения эллипса в Mathcad применяются параметрические уравнения вида:

x(t) = a·cos(t),

y(t) = b·sin(t),

где a и b – полуоси эллипса, t – параметр, изменяющийся от 0 до 2π.

В Mathcad задайте параметры a и b через переменные с конкретными значениями, например, a := 5, b := 3. Затем определите вектор параметра t, например:
t := 0, 0.01..2·π, что обеспечит достаточную точность построения.

Создайте функции для координат x(t) и y(t):

x(t) := a·cos(t),
y(t) := b·sin(t).

Для визуализации используйте график с параметрическими координатами, задав оси X и Y через полученные функции. Mathcad автоматически построит кривую по заданным точкам, что даст точное изображение эллипса.

Если необходимо изменить ориентацию эллипса, примените поворот с помощью матрицы вращения, модифицируя координаты:

x_rot(t) := x(t)·cos(θ) - y(t)·sin(θ),
y_rot(t) := x(t)·sin(θ) + y(t)·cos(θ),

где θ – угол поворота в радианах.

Для повышения плавности графика рекомендуется уменьшать шаг параметра t, но следует учитывать влияние на производительность Mathcad при слишком мелком разбиении.

Добавление сетки, подписей осей и форматирование графика

Для повышения читаемости построенного эллипса в Mathcad важно включить сетку и правильно оформить оси координат. Сначала активируйте сетку через меню графика: выберите «Свойства графика» → вкладка «Сетка» → отметьте «Показать сетку». Для более точного восприятия рекомендуются основные линии через 0.5 или 1 единицу, что задается параметрами «Основная сетка».

Подписи осей настраиваются в разделе «Оси». Укажите метки для оси X и Y в поле «Название оси», например, «X, мм» и «Y, мм» для метрической системы. Рекомендуется ограничить количество делений до 5–7, чтобы избежать загромождения. Значения осей задавайте вручную, если необходимо сфокусироваться на области эллипса, например, от –2 до 2.

Форматирование графика улучшает визуальное восприятие. Для линий эллипса установите толщину 2–3 пикселя и выберите насыщенный цвет, например, темно-синий. В случае нескольких графиков используйте разные стили линий – сплошные, пунктирные – для контраста. Размер шрифта подписей осей рекомендуют ставить в пределах 12–14 pt для читаемости без перегруженности.

Дополнительно включите отображение осей через опцию «Показать оси» для четкой ориентации. Если эллипс строится с помощью параметрического уравнения, добавьте точечные маркеры с шагом 0.2–0.3 для визуализации дискретных значений. Это помогает анализировать точность построения.

Итоговые настройки сохраняйте в шаблоне Mathcad для повторного использования, что ускоряет подготовку новых графиков и сохраняет единообразие оформления.

Сравнение эллипса с окружностью на одном графике

Для наглядного сопоставления эллипса и окружности в Mathcad важно построить обе фигуры в одной системе координат. Это позволяет визуально оценить различия в форме и размерах, а также понять особенности параметризации.

1. Определение параметров:
   • Эллипс: полуоси a и b, где a ≠ b.
   • Окружность: радиус r, равный одной из полуосей эллипса (обычно r = a или r = b).
2. Параметризация:
   • Эллипс: x = a * cos(t), y = b * sin(t).
   • Окружность: x = r * cos(t), y = r * sin(t).
3. Построение графика:
   • Задать одинаковый диапазон параметра t от 0 до 2π с мелким шагом (например, 0.01) для плавности линий.
   • Построить обе кривые в одной плоскости с разными цветами для визуального разделения.
   • Добавить легенду с обозначениями «Эллипс» и «Окружность».
4. Рекомендации по анализу:
   • Обратить внимание на участки, где эллипс отклоняется от окружности – это отражает разницу между полуосями.
   • Если a = b, эллипс совпадет с окружностью, что следует проверить для отладки параметров.
   • Использовать масштабирование осей с равными единицами для сохранения правильной геометрии.

Сравнение на одном графике позволяет быстро оценить степень деформации окружности в эллипс и понять влияние параметров a и b на форму.

Вопрос-ответ:

Как задать параметры эллипса в Mathcad для его построения?

Для построения эллипса в Mathcad сначала нужно определить основные параметры: длины большой и малой осей, а также координаты центра. Обычно задают значения полуосей a и b, а также центр (x0, y0). После этого можно использовать уравнения параметрической формы эллипса, где x = x0 + a*cos(t), y = y0 + b*sin(t), где t — параметр, изменяющийся от 0 до 2π. Эти формулы вводятся в Mathcad для построения графика.

Какие команды Mathcad применяются для построения графика эллипса?

Для отображения эллипса применяют команду построения графиков 2D. Сначала создают массив значений параметра t, обычно с равномерным шагом от 0 до 2π. Затем по формулам для x и y вычисляют соответствующие координаты. После этого в Mathcad используют функцию построения графика (например, «plot» или просто вставляют x(t) и y(t) в график) для отображения кривой. Важно, чтобы оба вектора были одинаковой длины.

Можно ли изменить ориентацию эллипса в Mathcad, если оси не совпадают с координатными?

Да, для этого применяют поворотные преобразования. Если угол наклона эллипса относительно осей координат равен θ, то новые координаты точек задаются через преобразование: x = x0 + a*cos(t)*cos(θ) — b*sin(t)*sin(θ), y = y0 + a*cos(t)*sin(θ) + b*sin(t)*cos(θ). В Mathcad достаточно добавить этот поворот к параметрическим уравнениям, чтобы получить эллипс, повернутый на нужный угол.

Какие ошибки часто встречаются при построении эллипса в Mathcad и как их избежать?

Одна из распространённых ошибок — неправильное определение диапазона параметра t или несоответствие размеров массивов x и y, что мешает построению графика. Также часто забывают правильно задать центр эллипса, что приводит к смещению фигуры. Чтобы избежать ошибок, необходимо тщательно проверить формулы, убедиться в правильности параметров, а также контролировать, чтобы значения параметра t покрывали весь интервал от 0 до 2π без пропусков.