Фазовый портрет – ключевой инструмент для анализа динамических систем, позволяющий визуализировать поведение решений дифференциальных уравнений на плоскости состояния. Mathcad предоставляет интегрированные средства для численного решения систем и построения графиков, что значительно упрощает процесс исследования.
В данном руководстве рассматривается методика создания фазового портрета для автономной системы двух дифференциальных уравнений с помощью стандартных функций Mathcad. Особое внимание уделено настройке сетки точек, выбору начальных условий и отображению векторов направления, что обеспечивает корректное и информативное визуальное представление.
Подготовка системы дифференциальных уравнений для анализа
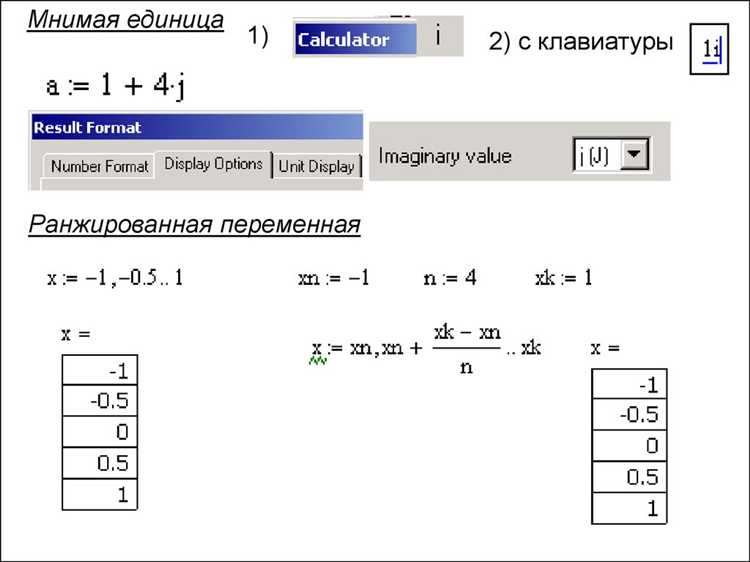
Первый этап построения фазового портрета в Mathcad – точное формулирование системы дифференциальных уравнений. Каждое уравнение должно быть выражено в виде явной функции производных, например, dx/dt = f(x, y), dy/dt = g(x, y). Неподходящими считаются уравнения в неявной форме, требующие дополнительного преобразования.
Рекомендуется заранее привести систему к автономному виду, то есть убрать явную зависимость от времени, если это возможно. Это существенно упрощает построение фазового портрета и анализ устойчивости точек равновесия.
Mathcad требует задать начальные условия для численного решения, поэтому их необходимо определить до моделирования. Для анализа критических точек удобно вычислить производные системы вручную или с помощью встроенных функций, а затем записать их в Mathcad для автоматического анализа.
Проверка размерностей и корректности функций f и g исключает ошибки, влияющие на поведение системы. Все параметры должны быть заданы числовыми значениями, без неопределенностей. Это гарантирует воспроизводимость результатов и корректное построение траекторий на фазовой плоскости.
Если система содержит параметры, целесообразно создать параметрическую модель, где значения легко изменяются. Mathcad поддерживает динамическое обновление решений при изменении параметров, что удобно для многократного анализа различных режимов.
В итоге, подготовленная система должна быть представлена в виде набора уравнений с числовыми параметрами и ясными начальными условиями, полностью готовых к интегрированию средствами Mathcad.
Настройка Mathcad для численного решения и графического отображения
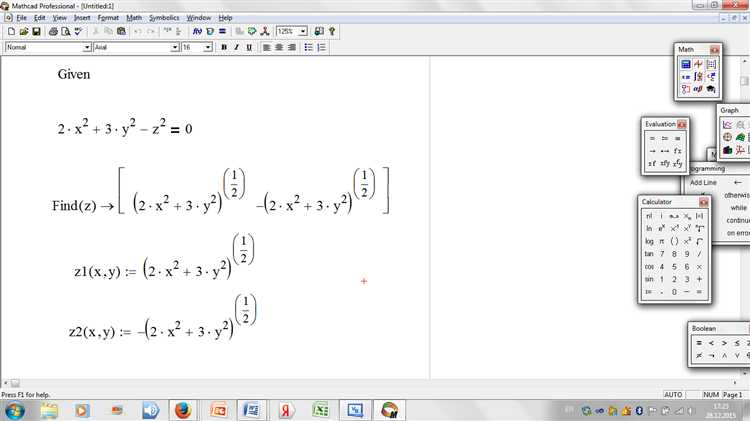
Для корректного численного решения дифференциальных уравнений в Mathcad необходимо предварительно задать параметры вычислительной области. В первую очередь определите интервал изменения переменной времени или независимой переменной через явное присваивание в виде вектора, например: t := 0, 0.01..10. Шаг сетки должен быть достаточно мал для точности, но не слишком мал, чтобы не увеличить время вычислений.
В разделе численного решения используйте встроенную функцию rkfixed или rkfixedstep для реализации метода Рунге–Кутты. Не забудьте задать начальные условия в формате вектора и определить правую часть системы как функцию от переменных состояния и времени.
Для построения фазового портрета используйте плоскостные графики, выбирая тип графика XY Plot. На оси X и Y следует отложить соответствующие переменные состояния. Чтобы избежать искажения, установите одинаковый масштаб по осям через опцию Equal Aspect Ratio.
Рекомендуется активировать сетку на графике для улучшения восприятия фазовой траектории. Настройте диапазон отображения графика вручную, задав значения через свойства осей, чтобы ограничить область визуализации и избежать пустого пространства.
Важный момент – отключите автоматическое масштабирование после первого построения, чтобы при изменении параметров системы или начальных условий график сохранял стабильность масштаба.
Для повышения скорости работы при большом объёме вычислений включите опцию Cache Results в настройках численного интегратора. Это позволяет избежать повторных расчётов при изменении только визуальных параметров.
В итоговой настройке используйте последовательность: определение сетки времени → настройка численного метода с указанием шага → задание начальных условий → построение XY-графика с равномерным масштабом и фиксированным диапазоном → включение сетки и кеширования.
Задание начальных условий и параметров системы в Mathcad
Начальные условия задаются через вектор состояния, например, x0 := [x1_0, x2_0], где x1_0 и x2_0 – значения переменных в момент времени t=0. В Mathcad это делается простым присваиванием с использованием квадратных скобок для векторов.
Параметры системы следует вводить отдельными переменными с понятными именами, например, a := 0.5, b := 1.2. Для удобства последующих вычислений рекомендуется группировать параметры в отдельный блок или использовать комментарии для их обозначения.
При использовании функций, описывающих динамику системы, необходимо убедиться, что начальные условия и параметры передаются корректно. Например, функция f(t, x, a, b) должна принимать на вход вектор состояния x и параметры a, b, чтобы внутри функции происходило правильное вычисление производных.
Вычисление траекторий решения методом численного интегрирования
В Mathcad реализована функция rkfixed для фиксированного шага метода Рунге-Кутты 4-го порядка, а также rksolve с адаптивным шагом. Для систем вида dx/dt = f(x, y), dy/dt = g(x, y) следует задать вектор функций и начальные условия в виде x(0), y(0).
Рекомендуется задавать шаг интегрирования h из диапазона 0.01–0.05 для обеспечения баланса между точностью и производительностью. Увеличение шага может привести к искажению траекторий или потере устойчивых решений.
Порядок действий:
- Определить систему в виде векторной функции F(t, X), где X = [x; y].
- Задать начальные условия X₀ – точки фазового пространства, откуда стартуют траектории.
- Выбрать интервал интегрирования по времени [t₀, t₁] с учетом динамики системы.
- Вызвать функцию интегрирования, например, rksolve(F, X₀, [t₀, t₁]) для получения численных значений.
- Сформировать набор точек траектории для последующей визуализации графика (x(t), y(t)).
Обязательно проверять устойчивость и корректность результатов, сравнивая несколько траекторий с различными начальными условиями и шагами интегрирования. При необходимости следует уменьшить шаг или использовать адаптивные методы.
Построение фазового портрета с помощью встроенных графических функций
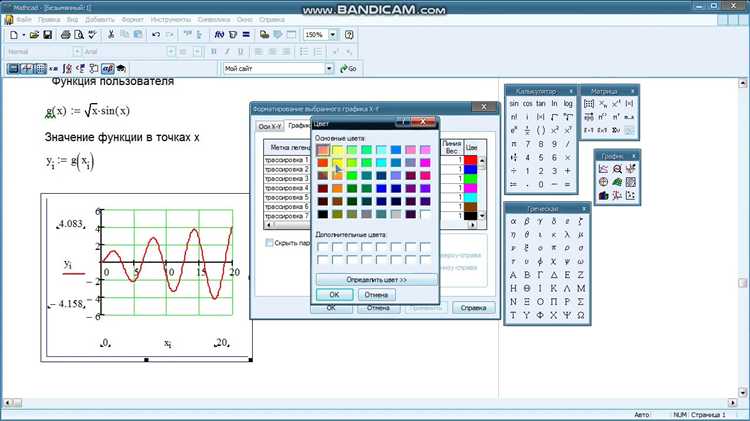
Для построения фазового портрета в Mathcad сначала необходимо задать систему дифференциальных уравнений в векторном виде. Рекомендуется использовать функцию ode для численного решения системы, задавая начальные условия через вектор начальных точек.
Далее примените функцию rkfixed или rk45 для интегрирования с фиксированным или адаптивным шагом, что позволяет контролировать точность и производительность вычислений. Результаты интегрирования сохраняются в массивы значений переменных по времени.
Для визуализации траекторий фазового пространства используйте функцию plot в режиме 2D или plot3d для систем с тремя переменными. Важным шагом является формирование набора начальных условий, охватывающих ключевые области фазового пространства, что позволяет получить полный обзор динамики.
Для наглядности наложите несколько траекторий на одном графике, используя разные цвета и маркеры через параметры функции plot. Это позволит выделить устойчивые и неустойчивые точки равновесия, а также устойчивые циклы.
Обязательно задавайте оси координат с равными масштабами, чтобы избежать искажений геометрии фазового портрета. Для этого в Mathcad настройте параметры осей вручную, указывая одинаковые интервалы для X и Y.
Использование функций arrow или vector помогает добавить направление движения на фазовом портрете, что особенно полезно для выявления направленности траекторий и устойчивости.
В завершение экспортируйте построенный график в векторный формат через меню Mathcad для последующего анализа или публикации. При работе с большими системами рекомендуется автоматизировать создание начальных условий и построение траекторий через встроенные циклы и массивы.
Анализ устойчивости и выявление точек равновесия на фазовом портрете
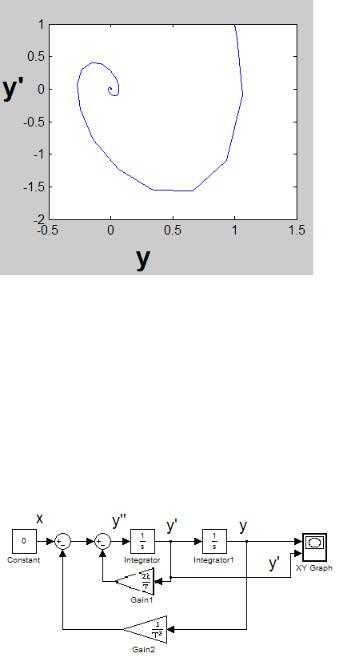
Для построения фазового портрета в Mathcad сначала необходимо определить точки равновесия системы, где производные по времени равны нулю. Это достигается решением системы уравнений вида:
- Записать уравнения динамической системы в виде dx/dt = f(x, y), dy/dt = g(x, y).
- Решить систему f(x, y) = 0 и g(x, y) = 0 методами численного решения или с помощью встроенных функций Mathcad.
После нахождения точек равновесия проводится их классификация по устойчивости с использованием матрицы Якоби, которая формируется из частных производных функций f и g по переменным x и y:
- J = [[∂f/∂x, ∂f/∂y], [∂g/∂x, ∂g/∂y]] в точках равновесия.
Далее необходимо вычислить собственные значения матрицы Якоби. В Mathcad это реализуется через функцию вычисления собственных значений матриц. Анализ устойчивости проводится по знакам вещественной части собственных значений:
- Если все вещественные части отрицательны – точка устойчива (аттрактор).
- Если хотя бы одна вещественная часть положительна – точка неустойчива.
- Если вещественные части равны нулю, проводится дополнительный анализ.
Для наглядности на фазовом портрете в Mathcad следует отметить точки равновесия и дополнительно построить векторы направления или траектории, исходящие из окрестностей этих точек. Это позволяет визуально подтвердить аналитические результаты устойчивости.
Рекомендуется для комплексного анализа дополнительно строить линии нулевого изменения (nullclines) по условиям f(x, y) = 0 и g(x, y) = 0, чтобы выявить взаимное расположение траекторий и точек равновесия.
Экспорт и сохранение результатов построения из Mathcad
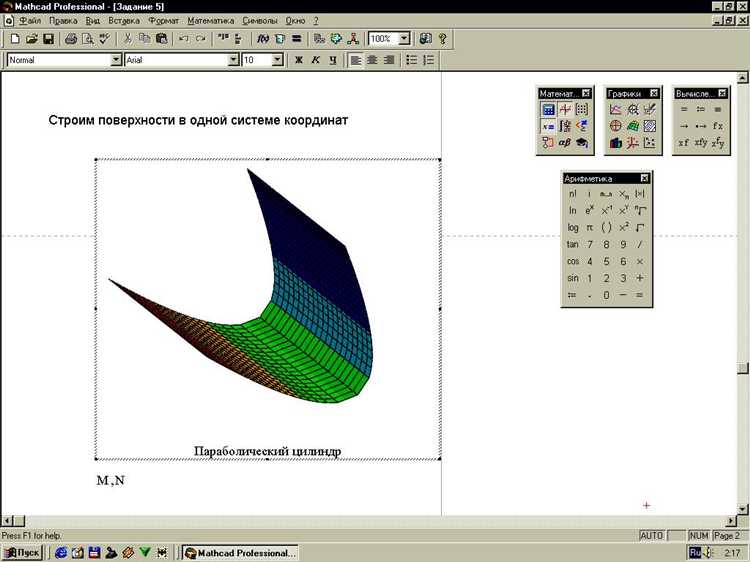
Для сохранения фазового портрета в Mathcad рекомендуется использовать встроенные функции экспорта графиков. Наиболее удобный формат для последующей обработки – PNG или SVG. После построения графика выделите область графика, кликните правой кнопкой и выберите «Сохранить как изображение».
В диалоговом окне укажите точное разрешение: для публикаций оптимально 300 dpi, для презентаций – 150 dpi. Формат SVG сохраняет векторное качество, что важно при масштабировании без потери четкости.
Если требуется экспорт данных фазового портрета для анализа, воспользуйтесь функцией экспорта данных из листа Mathcad. Для этого выделите необходимые таблицы или массивы данных, затем выберите «Файл» → «Экспорт» → «Текстовый файл» или CSV. Такой формат поддерживается большинством аналитических программ.
Для комплексного сохранения рекомендуется сохранить весь файл Mathcad с расширением .mcdx, что позволяет вернуться к исходным вычислениям и модифицировать параметры без потери данных.
При автоматизации экспорта можно использовать скрипты или макросы Mathcad, что ускорит процесс сохранения множества фазовых портретов с различными параметрами.
Вопрос-ответ:
Какие начальные данные нужны для построения фазового портрета в Mathcad?
Для построения фазового портрета в Mathcad необходимо задать систему дифференциальных уравнений, описывающих динамическую модель. Также требуется определить область определения переменных и выбрать начальные условия для численного решения. Важно учитывать параметры системы и их значения, так как они влияют на поведение траекторий на фазовой плоскости.
Как задать систему дифференциальных уравнений в Mathcad для построения фазового портрета?
В Mathcad систему дифференциальных уравнений задают с помощью функций, описывающих производные по времени каждой переменной. Для этого используют оператор производной (например, d/dt) и задают выражения в виде функций от переменных и параметров. После этого с помощью встроенных численных методов можно вычислить решение для заданных начальных условий и построить траектории на фазовой плоскости.
Какие методы численного решения применяются в Mathcad для фазового анализа и как их выбрать?
В Mathcad доступны разные численные методы, такие как метод Эйлера, метод Рунге-Кутты и другие встроенные алгоритмы решения дифференциальных уравнений. Для фазового анализа чаще всего применяют методы Рунге-Кутты, так как они обеспечивают хорошую точность при разумном времени вычислений. Выбор конкретного метода зависит от гладкости и жесткости системы, а также от требований к точности и скорости.
Как интерпретировать построенный фазовый портрет и определить устойчивость равновесных точек?
На фазовом портрете равновесные точки отображаются как точки, в которых траектории сходятся или расходятся. Чтобы оценить устойчивость, нужно проанализировать поведение траекторий около этих точек: если решения стремятся к точке при изменении времени, она устойчива; если отталкиваются — неустойчива. В Mathcad можно дополнительно вычислить якобиан системы в равновесных точках и проанализировать собственные значения для более формального определения устойчивости.
Как автоматизировать построение множества траекторий для фазового портрета в Mathcad?
Для создания множества траекторий задаются разные начальные условия в виде набора точек на фазовой плоскости. В Mathcad можно использовать циклы или матрицы начальных значений, после чего запускать численное решение для каждого из них. Полученные решения отображаются графически на одном координатном поле, что позволяет увидеть общее поведение системы и характер ее динамики.
Как в Mathcad построить фазовый портрет системы дифференциальных уравнений пошагово?
Для построения фазового портрета в Mathcad сначала необходимо записать систему дифференциальных уравнений в явном виде. Затем нужно определить область значений переменных и задать сетку точек, в которых будут вычисляться направления векторов. После этого для каждой точки рассчитываются значения производных, которые образуют вектор направления. Далее с помощью встроенных функций Mathcad отображаются эти векторы на плоскости. Завершающий этап — настройка графика для удобного просмотра, включая масштабирование и оформление осей. Таким образом, весь процесс разбит на понятные шаги, что облегчает понимание и применение метода.