Как построить фазовый портрет в matlab

Фазовый портрет – это инструмент визуализации динамики системы, определяемой системой дифференциальных уравнений. В Matlab для построения таких портретов удобно использовать функции ode45, quiver и plot. Конкретный выбор методов зависит от характера системы: линейная или нелинейная, автономная или неавтономная.

Для двумерной системы вида dx/dt = f(x, y), dy/dt = g(x, y) фазовый портрет отображается на плоскости (x, y) как поле направлений и траектории. В Matlab построение начинается с определения сетки значений переменных с помощью meshgrid и вычисления векторов правых частей уравнений. Далее используется quiver для отображения векторного поля и ode45 для численного интегрирования траекторий.

Ключевой момент – корректная нормализация векторов перед отрисовкой с помощью quiver: без неё векторное поле может терять читаемость. Также рекомендуется задавать несколько начальных условий для интегратора, чтобы получить полное представление о фазовой структуре. Использование axis equal позволяет избежать искажений при визуализации фазовых траекторий.

Для более сложных систем полезно реализовать функции, возвращающие правые части ОДУ, и визуализировать результат с помощью subplot при сравнении различных режимов. Это особенно эффективно при анализе бифуркаций и устойчивости решений.

Подготовка системы дифференциальных уравнений к численному решению

Перед численным решением необходимо привести систему к форме, совместимой с функциями ode45, ode23 и другими встроенными решателями MATLAB. Система должна быть записана как система первого порядка: каждая производная выражается явно через остальные переменные и независимую переменную (обычно время).

Если исходная модель включает уравнения второго порядка или выше, требуется преобразование. Например, уравнение d²x/dt² + 3dx/dt + 2x = 0 заменяется на систему:

dx1/dt = x2
dx2/dt = -2*x1 - 3*x2

где x1 = x, x2 = dx/dt. Далее, создается анонимная функция или отдельный файл с функцией в формате:

function dxdt = mySystem(t, x)
dxdt = zeros(2,1);
dxdt(1) = x(2);
dxdt(2) = -2*x(1) - 3*x(2);
end

Индексирование обязательно: переменные объединяются в вектор состояния x. Размер вектора должен соответствовать числу уравнений. Внутри функции запрещено использовать глобальные переменные – параметры системы передаются через вложенные функции или function handle с параметрами.

Необходимо проверять линейность и жесткость системы. Жесткие системы лучше решать с использованием ode15s или ode23s. Нелинейные системы должны быть стабилизированы (при необходимости – линеаризованы) перед вычислением фазового портрета, особенно в окрестности равновесных точек.

Начальные условия должны быть заданы с учетом физических или математических ограничений задачи. Например, для системы маятника: x(1) – угол, x(2) – угловая скорость. Неверно заданные начальные значения могут исказить поведение траекторий на фазовом портрете.

Перед запуском ode-решателя проводится проверка размерностей, тестовая симуляция на коротком интервале и оценка устойчивости полученных траекторий. Ошибки округления и особенности поведения системы (разрывы, сингулярности) выявляются на этом этапе.

Определение области фазового пространства и построение сетки начальных условий

Перед построением фазового портрета необходимо задать границы фазового пространства. Эти границы определяются диапазонами переменных системы: например, для системы второго порядка с переменными x и ẋ (положение и скорость), необходимо задать диапазоны значений для обеих осей.

Рекомендуется выбирать диапазон на основе анализа уравнений движения или предварительного численного эксперимента. Например, для осциллятора с параметрами, допускающими колебания в пределах ±5 по координате и ±10 по скорости, целесообразно использовать диапазоны x ∈ [-5, 5] и ẋ ∈ [-10, 10]. Это исключает область, не участвующую в динамике, и уменьшает вычислительные затраты.

Для построения сетки начальных условий удобно использовать функции meshgrid или ndgrid. Шаг сетки должен быть достаточным для отображения структуры потока, но не чрезмерным, чтобы избежать перегрузки графика. Например, при шаге 1 для каждой переменной:


[x0, dx0] = meshgrid(-5:1:5, -10:2:10);

Полученные матрицы x0 и dx0 содержат координаты начальных условий, которые можно использовать в цикле интегрирования для построения траекторий:


for i = 1:numel(x0)
[t, sol] = ode45(@(t, y) f(t, y), [0, T], [x0(i); dx0(i)]);
plot(sol(:,1), sol(:,2), 'b');
hold on;
end

Для систем более высокого порядка фазовое пространство расширяется: при наличии трёх переменных (x, ẋ, ẍ) необходимо фиксировать одну из них или использовать проекции. В таком случае сетка строится только по двум переменным, а третья задаётся как параметр.

Использование функции ode45 для численного интегрирования траекторий

Функция ode45 в Matlab реализует метод Рунге–Кутты 4–5 порядка с адаптивным шагом и оптимально подходит для решения нежестких систем обыкновенных дифференциальных уравнений. Для построения фазового портрета, она используется для вычисления траекторий в пространстве состояний при различных начальных условиях.

Стандартный вызов функции:

[t, y] = ode45(@(t, y) f(t, y), tspan, y0);

f(t, y) – функция, задающая систему уравнений dy/dt = f(t, y). Возвращает вектор той же размерности, что и y.
tspan – вектор [t0 tf] с начальным и конечным моментом времени.
y0 – вектор начальных условий. Размерность должна соответствовать размерности системы.

Рекомендации по применению:

Для автономных систем, переменная времени t может быть неиспользуема внутри f. Однако, она обязана присутствовать в сигнатуре функции.
Определяйте функцию f как вложенную или анонимную, чтобы избежать избыточных глобальных переменных.
Для повышения точности фазового портрета, интегрируйте с большим интервалом времени tspan и используйте начальные условия, охватывающие ключевые области фазового пространства.
Для сложных систем задавайте options = odeset(...) с параметрами 'RelTol' и 'AbsTol', чтобы контролировать точность решения.
После получения решения используйте команды plot(y(:,1), y(:,2)) для построения траекторий в фазовой плоскости.

Пример для системы: dx/dt = y, dy/dt = -x - 0.1*y


f = @(t, z) [z(2); -z(1) - 0.1*z(2)];
[t, z] = ode45(f, [0 50], [1 0]);
plot(z(:,1), z(:,2));
xlabel('x'); ylabel('y');
grid on;

Такой подход позволяет получить точные и устойчивые фазовые траектории даже при длинных интервалах интегрирования.

Визуализация траекторий с помощью функции plot в двумерном пространстве

Для построения фазового портрета в двумерной системе обыкновенных дифференциальных уравнений применяется функция plot, позволяющая отображать траектории движения в пространстве состояний. Ниже приведены конкретные рекомендации для эффективной визуализации.

Перед использованием plot необходимо численно решить систему уравнений с помощью ode45 или другой подходящей функции интегрирования. Пример:
```
[t, Y] = ode45(@(t, y) [y(2); -0.5*y(2) - sin(y(1))], [0, 20], [1; 0]);
```
Для отображения траектории используется:
```
plot(Y(:,1), Y(:,2), 'b-');
```
где Y(:,1) – значения переменной x, Y(:,2) – значения dx/dt.
Рекомендуется задавать цвет и тип линии для различения множественных траекторий. Например:
```
plot(Y(:,1), Y(:,2), 'r--');
```
Для отображения нескольких траекторий с разными начальными условиями используйте цикл:
```
hold on;
for x0 = -2:1:2
for v0 = -2:1:2
[~, Y] = ode45(@(t, y) [y(2); -y(1)], [0, 10], [x0; v0]);
plot(Y(:,1), Y(:,2));
end
end
hold off;
```
Добавляйте подписи осей:
```
xlabel('x');
ylabel('dx/dt');
```
Для выделения направлений движения вдоль траекторий используйте функцию quiver или отрисовку стрелок вручную:
```
plot(Y(:,1), Y(:,2));
hold on;
quiver(Y(1:10:end,1), Y(1:10:end,2), ...
diff(Y(1:10:end,1)), diff(Y(1:10:end,2)), 0);
hold off;
```

Функция plot обеспечивает гибкость и точность при визуализации фазовых траекторий, особенно при корректной настройке начальных условий и масштабов.

Добавление стрелок направления движения с использованием функции quiver

Для визуализации направления движения в фазовом пространстве применяют функцию quiver, которая отображает векторы поля скоростей в каждой точке сетки. Перед вызовом quiver необходимо создать равномерную сетку и вычислить производные системы в каждой точке этой сетки.

Пример построения фазового портрета для системы:

dx/dt = y; dy/dt = -x - y;

Генерация сетки и векторного поля:


[x, y] = meshgrid(-5:0.5:5, -5:0.5:5);
u = y;
v = -x - y;

Нормировка векторов для визуальной ясности:


L = sqrt(u.^2 + v.^2);
u = u ./ L;
v = v ./ L;

Построение стрелок:


quiver(x, y, u, v, 0.5, 'k');
axis equal;
xlabel('x');
ylabel('y');

Параметр 0.5 масштабирует длину стрелок без изменения направления. Цвет ‘k’ – черный, обеспечивает контраст с траекториями. Важно выбирать плотность сетки, достаточную для передачи структуры поля, но не перегружающую изображение. Для сложных систем возможно использование сглаживания или маскирования векторов по модулю производной.

Создание фазового портрета для нелинейной системы уравнений

Рассмотрим построение фазового портрета в Matlab для системы второго порядка:

dx/dt = y
dy/dt = -0.5*y - sin(x)

Определим правые части системы в виде анонимной функции:

f = @(t, z) [z(2); -0.5*z(2) - sin(z(1))];

Создадим сетку начальных условий в интересующей области фазового пространства:

[X, Y] = meshgrid(-3:0.5:3, -3:0.5:3);

На каждой точке сетки вычислим вектор поля:

U = Y;
V = -0.5*Y - sin(X);

Отнормируем векторы для равномерного отображения стрелок:

L = sqrt(U.^2 + V.^2);
U = U./L;
V = V./L;

Построим фазовый портрет с помощью команды quiver:

quiver(X, Y, U, V, 0.5, 'k');
axis equal; grid on;
xlabel('x'); ylabel('y');

Добавим траектории системы с помощью ode45. Зададим начальные условия:

hold on;
for x0 = -2:1:2
    for y0 = -2:1:2
        [t, z] = ode45(f, [0 20], [x0; y0]);
        plot(z(:,1), z(:,2), 'b');
    end
end

Анализ полученного портрета позволяет визуально оценить устойчивость и характер движения вблизи равновесия. Изменяя параметры системы, можно наблюдать бифуркации и смену режимов.

Автоматизация построения фазового портрета через пользовательскую функцию

Для систематизации и ускорения построения фазовых портретов в Matlab целесообразно использовать пользовательскую функцию, принимающую векторную функцию правых частей ОДУ, диапазоны значений и параметры визуализации. Это исключает дублирование кода при анализе различных систем.

Создайте файл phasePortrait.m со следующим содержанием:

function phasePortrait(f, xRange, yRange, x0grid, y0grid, tspan)
[X0, Y0] = meshgrid(x0grid, y0grid);
hold on
for i = 1:numel(X0)
[~, sol] = ode45(@(t, y) f(t, y), tspan, [X0(i); Y0(i)]);
plot(sol(:,1), sol(:,2), 'b')
end
xlabel('x')
ylabel('y')
axis([xRange yRange])
grid on
hold off
end

Параметры:

f – функция системы (например, @(t, y)[y(2); -0.5*y(2) - y(1)])

xRange, yRange – границы отображения, например, [-5 5]

x0grid, y0grid – массивы начальных условий (например, -4:1:4)

tspan – интервал интегрирования, например, [0 20]

Вызов функции для построения фазового портрета:

f = @(t, y) [y(2); -0.5*y(2) - y(1)];
phasePortrait(f, [-5 5], [-5 5], -4:1:4, -4:1:4, [0 20])

Для повышения наглядности добавьте поле направлений с помощью quiver перед циклом:

[X, Y] = meshgrid(linspace(xRange(1), xRange(2), 20), linspace(yRange(1), yRange(2), 20));
U = zeros(size(X));
V = zeros(size(Y));
for i = 1:numel(X)
dydt = f(0, [X(i); Y(i)]);
U(i) = dydt(1);
V(i) = dydt(2);
end
quiver(X, Y, U, V, 'r')

Такой подход обеспечивает повторяемость результатов и удобство в исследовании различных динамических систем без переписывания графических процедур.

Экспорт графика фазового портрета в виде изображения или PDF-файла

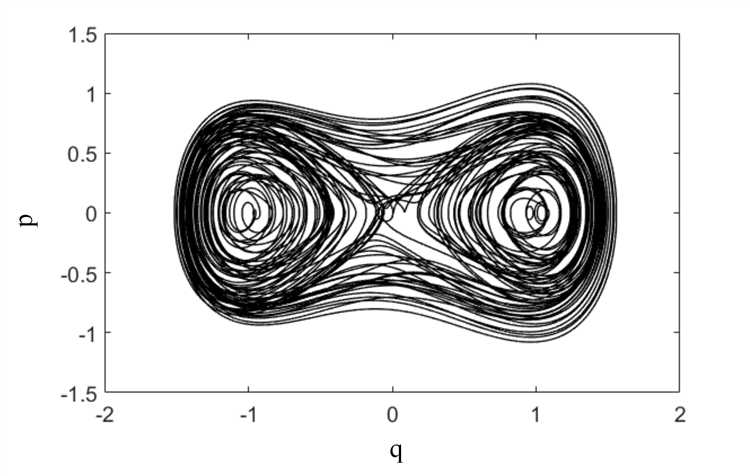
Для сохранения фазового портрета из MATLAB используйте команду saveas или exportgraphics. Последняя предпочтительна, если требуется высокое качество и контроль параметров.

Чтобы экспортировать график в PNG:

exportgraphics(gca, 'phase_portrait.png', 'Resolution', 300);

Для сохранения в PDF:

exportgraphics(gca, 'phase_portrait.pdf', 'ContentType', 'vector');

Если используется figure с несколькими осями, вместо gca укажите нужный объект осей, например ax, полученный ранее: ax = axes;

Команда saveas менее гибкая и может приводить к потере качества при экспорте в растровые форматы:

saveas(gcf, 'phase_portrait.jpg');

Чтобы задать размеры и ориентацию PDF, используйте set с PaperPosition и PaperOrientation перед вызовом print:

set(gcf, 'PaperUnits', 'inches', 'PaperPosition', [0 0 6 4], 'PaperOrientation', 'landscape'); print(gcf, 'phase_portrait', '-dpdf', '-r300');

Для прозрачного фона при экспорте в PNG используйте параметр 'BackgroundColor','none':

exportgraphics(gca, 'phase_portrait.png', 'BackgroundColor','none');

Проверьте сохранённый файл, открыв его в стороннем просмотрщике, чтобы убедиться в правильной цветопередаче и читаемости всех элементов графика.