Для построения графика функции в Maple необходимо использовать команду plot, которая позволяет визуализировать аналитические выражения с точным заданием интервала переменной. Например, для функции f(x) = sin(x) график строится командой plot(sin(x), x = 0..2*Pi). Важно корректно определить область построения, чтобы увидеть ключевые особенности графика.
Maple поддерживает не только функции одной переменной, но и параметрические уравнения, системы и неявные функции. Для неявных уравнений применяется команда implicitplot из пакета plots. Например, уравнение окружности x^2 + y^2 = 1 визуализируется как implicitplot(x^2 + y^2 = 1, x = -1..1, y = -1..1). Настройка диапазонов по обеим осям гарантирует корректное отображение.
При работе с Maple рекомендуется задавать явные переменные и интервал построения, а также использовать дополнительные параметры для управления видом графика – толщиной линий, цветом и отображением сетки. Это позволяет сделать визуализацию более информативной и наглядной для анализа.
Подготовка уравнения к построению графика в Maple
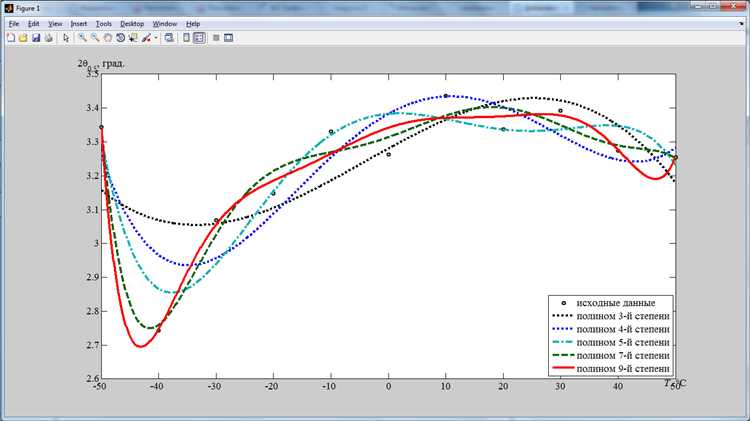
Перед построением следует проверить правильность записи уравнения с учетом синтаксиса Maple. Все операции должны быть явно указаны: умножение – с символом *, возведение в степень – с ^. Не допускается использование математических сокращений, непонятных системе, например, xy вместо x*y.
Для дробных выражений предпочтительно применять скобки, чтобы избежать неоднозначностей. Например, выражение (x + 1)/(x — 2) будет корректно воспринято. В случае использования корней рекомендуется заменить корень на степень с дробным показателем, например, sqrt(x) на x^(1/2), если это удобнее.
Перед построением полезно проверить уравнение на наличие параметров или констант. Для упрощения графика параметры лучше заменить числовыми значениями. Если параметры остаются, необходимо явно задать их значения через команду assign или в скрипте.
В случае работы с тригонометрическими функциями важно помнить, что Maple воспринимает углы в радианах по умолчанию. Если уравнение задано в градусах, необходимо выполнить преобразование: например, заменить sin(x) на sin(x*Pi/180).
Если уравнение содержит несколько переменных, но требуется построить график в двух измерениях, необходимо зафиксировать значения всех переменных, кроме двух, которые будут по осям. Для трехмерных графиков используются соответствующие функции plot3d или implicitplot3d.
Использование команды plot для построения графика функции
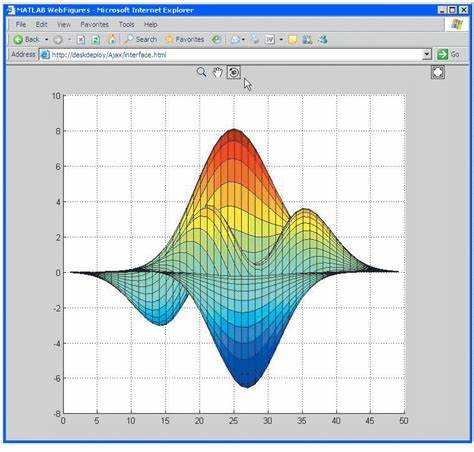
Команда plot в Maple служит для визуализации функций одной переменной. Для построения графика указывается функция и интервал переменной. Формат базового вызова: plot(f(x), x = a..b), где f(x) – выражение функции, a и b – границы интервала.
Для точного отображения графика важно корректно выбрать интервал. Если функция содержит особенности, например, разрывы или точки перегиба, рекомендуется сузить область построения или использовать дополнительные параметры для управления плотностью точек.
Параметр numpoints увеличивает количество вычисляемых точек, что повышает точность графика. Например, plot(sin(x), x=0..2*Pi, numpoints=1000) обеспечит гладкость кривой.
Возможна настройка внешнего вида: цвет и тип линии задаются через опции color и style. Например, plot(x^2, x=-2..2, color=red, style=point) отобразит график красными точками.
Для построения нескольких функций одновременно используется синтаксис plot([f1(x), f2(x)], x=a..b). Maple автоматически подберет цвета для каждого графика.
Если функция задана в виде неявного уравнения, для построения графика применяют команду implicitplot из пакета plots. Но для явных функций plot остается наиболее быстрым и удобным инструментом.
Построение графика неявного уравнения с помощью implicitplot
Для построения графика неявного уравнения в Maple используется команда implicitplot из пакета plots. Она позволяет визуализировать уравнения вида F(x, y) = 0, где y не выражена явно через x.
Основные шаги построения:
- Подключите пакет командой
with(plots):. - Сформулируйте неявное уравнение в формате
F(x, y) = 0. - Вызовите
implicitplot, указав уравнение и диапазоны переменныхxиy.
Пример вызова:
implicitplot(x^2 + y^2 = 1, x = -2 .. 2, y = -2 .. 2);
Рекомендации для корректного построения:
- Выбирайте диапазоны переменных с запасом, чтобы график полностью помещался на экране.
- Для уравнений с несколькими ветвями увеличивайте плотность точек через параметр
grid, напримерgrid = [100, 100]. - Используйте опцию
colorдля выделения графика цветом, напримерcolor = red. - Если уравнение содержит параметры, задавайте их заранее через команду
subsили определяйте как значения в отдельной строке. - Для сложных уравнений можно повысить точность построения, увеличивая параметры
resolutionиgridrefine.
Пример с дополнительными опциями:
implicitplot(x^3 + y^3 - 3*x*y = 0, x = -2 .. 2, y = -2 .. 2, grid = [150, 150], color = blue, thickness = 2);
Настройка области построения графика и масштаба осей
В Maple область построения графика задаётся параметрами диапазона по каждой оси, передаваемыми в функции построения графика. Для двумерных графиков используйте опцию view=[xmin..xmax, ymin..ymax], где xmin, xmax, ymin и ymax – числовые значения границ отображения.
Например, для построения графика функции f:=x->sin(x) на интервале от 0 до 2π по оси X и от -1.5 до 1.5 по оси Y вызов будет выглядеть так: plot(f(x), x=0..2*Pi, view=[0..2*Pi, -1.5..1.5]).
Если масштаб по осям должен быть одинаковым, используйте параметр scaling=constrained. Это гарантирует, что единичный отрезок по X и Y будет одинаковой длины, что важно для геометрических фигур.
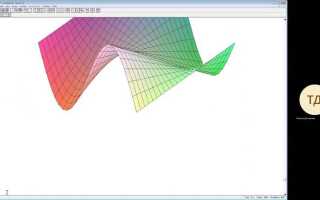
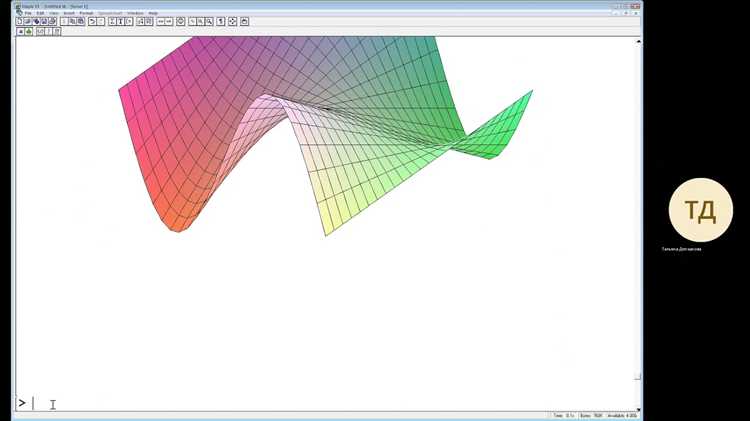
Для трёхмерных графиков аналогично задаётся диапазон через опцию view=[xmin..xmax, ymin..ymax, zmin..zmax]. Пример: plot3d(x^2 - y^2, x=-2..2, y=-2..2, view=[-2..2, -2..2, -5..5]).
Дополнительно можно управлять количеством делений осей и их метками с помощью опции axes=boxed или axes=frame, а также параметра ticks, который позволяет задать расположение и формат меток вручную.
Добавление нескольких графиков на один рисунок в Maple
Для отображения нескольких функций на одном рисунке в Maple применяется оператор plots[display] из пакета plots. Сначала строятся отдельные графики каждой функции с помощью команды plot, после чего они объединяются в единый объект для совместного отображения.
Пример создания двух графиков и их объединения:
with(plots):
p1 := plot(sin(x), x = -Pi .. Pi, color = red):
p2 := plot(cos(x), x = -Pi .. Pi, color = blue):
display([p1, p2]);
Рекомендуется явно задавать область построения для всех графиков, чтобы они совпадали по осям. Для контроля осей можно использовать параметры view и axes.
Для увеличения информативности при совмещении графиков полезно добавить легенду. Это делается с помощью опции legend:
display([p1, p2], legend = ["sin(x)", "cos(x)"], legendstyle = [location = top]);
Для построения большего количества функций достаточно расширить список графиков в display. Если функции задаются в цикле, удобно формировать список с графиками программно и передавать его в display.
Пример для трёх функций с автоматическим созданием списка:
funcs := [sin(x), cos(x), tan(x)]:
plots_list := [seq(plot(funcs[i], x = -Pi .. Pi, color = i), i = 1 .. 3)]:
display(plots_list, legend = ["sin(x)", "cos(x)", "tan(x)"], legendstyle = [location = right]);
Использование plots[display] обеспечивает сохранение параметров каждого графика (цвет, стиль линий, область построения) и удобство управления общим отображением.
Изменение цвета, толщины и стиля линий графика
В Maple параметры визуального оформления графика регулируются с помощью опций, передаваемых в функцию plot. Для изменения цвета линии используется параметр color. Значение можно указать как стандартное название цвета в кавычках, например, color="red", или RGB-массив, например, color=[0,0,1] для синего.
Толщина линии настраивается через параметр thickness, который принимает числовое значение. По умолчанию используется значение 1, увеличение до 3–5 сделает линию более заметной. Например, thickness=3.
Стиль линии задаётся с помощью параметра style. Значения включают solid (сплошная), dot (пунктирная), dash (штриховая), dotdash (штрих с точкой). Пример: style=dash изменит линию на штриховую.
Для комбинирования параметров они перечисляются через запятую внутри вызова plot. Пример построения графика функции sin(x) с красной, толщиной 2 и штриховой линией:
plot(sin(x), x=-2*Pi..2*Pi, color="red", thickness=2, style=dash);
Для нескольких функций можно использовать список списков параметров, где каждому графику назначается свой набор цветов и стилей. Это упрощает восприятие при построении нескольких кривых.
Сохранение и экспорт графиков из Maple в популярные форматы
Для сохранения графика в Maple после построения необходимо использовать команду plots[display] для формирования графического объекта, а затем функцию exportplot или встроенную команду экспорта из меню. Основные форматы для сохранения – PNG, PDF, SVG и EPS.
Команда для экспорта графика в файл выглядит так: exportplot(graph, "имя_файла.формат"), где graph – объект графика, созданный в Maple. При указании расширения файла Maple автоматически выберет соответствующий формат.
PNG оптимален для веб-публикаций и презентаций благодаря поддержке прозрачности и сжатию без потерь. Рекомендуется задавать разрешение не менее 300 dpi для качественной печати через параметр resolution=300.
PDF и EPS подходят для векторной графики, сохраняющей качество при масштабировании. Векторные форматы предпочтительны для публикаций и научных работ. Экспорт в PDF осуществляется через команду exportplot(graph, "имя_файла.pdf") без потери качества элементов графика.
SVG удобен для интеграции в веб-документы и позволяет редактировать графику в редакторах типа Inkscape. Maple сохраняет SVG с сохранением всех элементов построения, что обеспечивает точность и гибкость.
При экспорте важно учитывать размер области построения (plot region), чтобы избежать обрезки элементов. Для этого стоит настраивать параметры view и scaling перед сохранением.
Автоматизация процесса экспорта с помощью скриптов в Maple упрощает массовое сохранение множества графиков в различных форматах, что полезно при подготовке больших отчетов и презентаций.
Вопрос-ответ:
Как задать уравнение для построения графика в Maple?
Для построения графика в Maple необходимо ввести уравнение как выражение, используя стандартный синтаксис. Например, чтобы построить график функции y = x^2, нужно написать y := x -> x^2; затем вызвать команду plot(y, x=a..b), где a и b — границы интервала по оси x. Важно правильно указать переменные и использовать стрелку для определения функции.
Можно ли в Maple строить графики неявных уравнений, например, x^2 + y^2 = 1?
Да, в Maple предусмотрена возможность строить графики неявных уравнений. Для этого используется команда implicitplot из пакета plots. Сначала подключают пакет командой with(plots); затем вызывают implicitplot(x^2 + y^2 = 1, x = -1..1, y = -1..1); Этот способ позволяет отображать кривые, заданные уравнениями, где y явно не выражена через x.
Как изменить масштаб и область отображения графика в Maple?
Изменение масштаба и области отображения выполняется через параметры команды plot. В качестве второго аргумента указывают диапазон значений переменной, например, plot(sin(x), x = -Pi..Pi). Чтобы настроить область по оси y, можно использовать опцию view, например, plot(x^2, x = -2..2, view = [0..4]); Таким образом задаются границы по обеим осям, что помогает лучше рассмотреть нужный участок графика.
Как построить в Maple график нескольких функций на одном рисунке?
Для отображения нескольких функций на одном графике в Maple используют команду plot с передачей списка функций через запятую, например: plot([sin(x), cos(x), x^2], x = -Pi..Pi). Все функции будут отображены разными цветами, и можно добавлять легенду с помощью опции legend, например, plot([sin(x), cos(x)], x = 0..2*Pi, legend = [«sin(x)», «cos(x)»]). Такой способ удобен для сравнения нескольких функций в одном координатном пространстве.