Как построить полином лагранжа в maple

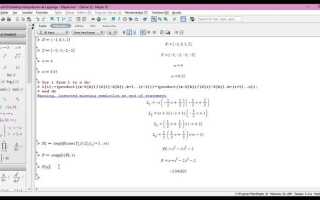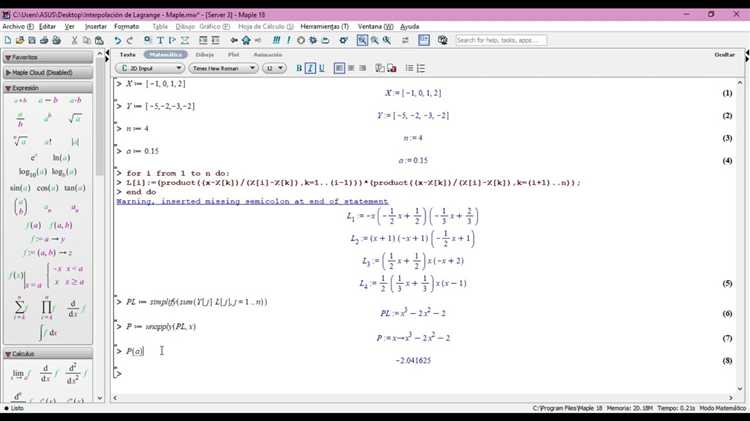
Полином Лагранжа – один из основных инструментов интерполяции в численных методах. В системе компьютерной алгебры Maple его построение требует точного определения исходных данных и корректного применения встроенных функций. Рассмотрим, как с помощью Maple эффективно построить интерполяционный многочлен по заданному набору узлов.

Пусть заданы узлы интерполяции x₀, x₁, …, xₙ и соответствующие значения функции f(x₀), f(x₁), …, f(xₙ). В Maple они могут быть представлены в виде списка пар [xᵢ, fᵢ]. Построение полинома Лагранжа возможно через ручное задание формулы или с использованием библиотеки CurveFitting. В последнем случае применяется функция LagrangeInterpolation, принимающая список точек и возвращающая аналитическое выражение интерполяционного многочлена.

Для точной работы с выражением рекомендуется использовать команду simplify после построения полинома, так как Maple по умолчанию возвращает результат в развёрнутом виде. Это позволяет получить компактное представление результата, удобное для дальнейшего анализа или дифференцирования. При необходимости вычисления значений полинома в конкретных точках применяется подстановка через оператор subs или функция eval.

Использование Maple позволяет не только строить полином Лагранжа, но и визуализировать его график на фоне исходных точек. Для этого применяется функция plot с передачей как аналитического выражения, так и координат точек, что обеспечивает наглядную проверку точности интерполяции.

Как задать таблицу узлов интерполяции в Maple

Для задания узлов интерполяции в Maple необходимо определить два списка: координаты по оси x и соответствующие значения функции y. В Maple это выполняется с помощью списков или массивов.

Пример с использованием списков:


X := [1, 2, 3, 4];
Y := [2.5, 3.1, 5.6, 7.8];


Если требуется создать ассоциативный список пар (x, y), используйте список списков:


nodes := [[1, 2.5], [2, 3.1], [3, 5.6], [4, 7.8]];


Для использования с встроенными функциями интерполяции, например Interpolation из пакета CurveFitting, необходимо передать список точек в виде:


with(CurveFitting):
Interpolation([[1, 2.5], [2, 3.1], [3, 5.6], [4, 7.8]], x);


В случае построения полинома Лагранжа вручную, предпочтительно разделять X и Y как отдельные списки, чтобы при необходимости обращаться к ним по индексам:


n := nops(X);
for i from 1 to n do
  xi := X[i];
  yi := Y[i];
  # дальнейшие вычисления
od;


Индексирование в Maple начинается с 1. Внимательно следите за длиной списков X и Y, они должны быть одинаковыми. Несовпадение размеров приведёт к ошибкам при вычислениях.

Пошаговое построение базисных полиномов Лагранжа

Рассмотрим набор узлов интерполяции: \( x_0, x_1, \dots, x_n \). Базисный полином Лагранжа для узла \( x_i \) определяется как:

\[

L_i(x) = \prod_{\substack{0 \le j \le n \\ j \ne i}} \frac{x — x_j}{x_i — x_j}

\]

В Maple для каждого \( L_i(x) \) необходимо:

1. Ввести список узлов:

X := [x0, x1, x2, ..., xn];

2. Задать переменную:

x := 'x';

3. Реализовать формулу через цикл или списковое выражение. Пример для одного базисного полинома \( L_i(x) \):


L := i -> mul((x - X[j]) / (X[i] - X[j]), j = 1 .. nops(X)) assuming j <> i;


Однако в Maple условие j <> i в пределах mul игнорируется, поэтому лучше использовать фильтрацию через select или создать отдельный список индексов:


L := i -> mul((x - X[j]) / (X[i] - X[j]), j in [seq(j, j = 1 .. nops(X)) | j <> i]);


4. Для вычисления всех базисных полиномов используйте:


L_set := [seq(L(i), i = 1 .. nops(X))];


5. Упростите выражения через simplify, особенно при численных значениях:


L_simplified := map(simplify, L_set);


Все базисные полиномы \( L_i(x) \) можно использовать для построения интерполяционного полинома по формуле Лагранжа, подставив значения функции в узлах.

Формирование итогового интерполяционного полинома

Для построения итогового полинома Лагранжа в Maple необходимо последовательно выполнить вычисления базисных полиномов и их линейную комбинацию с учетом заданных значений функции. Предположим, даны узлы интерполяции x₀, x₁, …, x_n и соответствующие значения f(x₀), f(x₁), …, f(x_n). Далее выполняются следующие шаги:

1. Объявить список узлов и значений функции:

   X := [x0, x1, x2, ..., xn]; Y := [y0, y1, y2, ..., yn];

2. Определить базисные полиномы Лагранжа:

   L := (i, X, x) -> mul((x - X[j])/(X[i] - X[j]), j=1..n) assuming j <> i;
   

3. Сформировать итоговый полином как сумму:

   P := add(Y[i]*L(i, X, x), i=1..n);
   

4. Упростить полученное выражение:

   simplify(P);

В Maple индексация начинается с 1. Если узлы заданы вручную, использовать X := [1, 2, 3], Y := [4, 9, 16]. Для автоматизации рекомендуется использовать цикл или встроенные процедуры. После получения выражения P его можно проанализировать, продифференцировать, интегрировать или построить график при помощи plot(P, x=a..b).

Важно: при большом числе узлов избежать символьного взрыва поможет использование evalf(P) для численного представления полинома. Для точной работы с рациональными числами – использовать convert(P, rational).

Проверка совпадения полинома с заданными точками

После построения интерполяционного полинома Лагранжа в Maple необходимо убедиться, что полученное выражение точно проходит через все исходные точки. Для этого воспользуйтесь командой subs для подстановки координат точек в полином и сравнения результата с соответствующими значениями ординат.

Пусть полином обозначен как P, а множество точек задано в виде списка pts := [[x1, y1], [x2, y2], …, [xn, yn]]. Для проверки каждой точки выполните:

evalf(subs(x=xi, P)) = yi

Для автоматизации создайте цикл:


for pt in pts do
  xval := pt[1];
  yval := pt[2];
  if evalf(subs(x=xval, P)) <> yval then
    print("Несовпадение в точке", pt);
  end if;
end do;


Если проверка выявляет несовпадения, убедитесь в корректности ввода точек и отсутствии численных ошибок. Для точных вычислений рекомендуется использовать рациональные числа, а не числа с плавающей запятой. Замените evalf на simplify при работе с точными выражениями:

simplify(subs(x=xi, P) - yi) = 0

Точное совпадение подтверждает корректность интерполяции. Любые отклонения требуют пересмотра построения полинома или исходных данных.

Графическая визуализация полинома Лагранжа в Maple

Для построения графика полинома Лагранжа в Maple используется функция plot совместно с ранее определённым полиномом. Предположим, что полином L(x) уже построен с использованием процедуры интерполяции по заданным узлам.

Пример определения интерполяционного полинома по узлам X := [1, 2, 4] и значениям Y := [2, 3, 1]:

X := [1, 2, 4]:
Y := [2, 3, 1]:
L := add(Y[i]*mul((x - X[j])/(X[i] - X[j]), j = 1..nops(X)) , i = 1..nops(X)):

Для визуализации полинома используйте следующую команду:

plot([L, [seq([X[i], Y[i]], i = 1..nops(X))]], x = min(X)-1 .. max(X)+1,
color = [red, black], style = [line, point], symbol = solidcircle, thickness = 2);

Данная команда отображает полином Лагранжа красной линией, а исходные точки интерполяции – чёрными маркерами. Параметр thickness улучшает визуальное восприятие кривой. Символ solidcircle обеспечивает чёткое обозначение узлов.

Для наглядного сравнения нескольких полиномов (например, при изменении числа узлов), можно использовать множественный график:

plot([L1, L2], x = a .. b, color = [blue, green], linestyle = [solid, dash]);

Границы области визуализации следует подбирать с учётом диапазона узлов, чтобы не искажать форму полинома. При большом количестве узлов рекомендуется избегать чрезмерного увеличения масштаба, так как это приводит к визуальным артефактам осцилляций (эффект Рунге).

Для автоматизации построения и визуализации рекомендуется оформлять процесс в виде процедуры, принимающей массивы узлов и значений на вход и возвращающей график.

Работа с символьными и числовыми узлами интерполяции

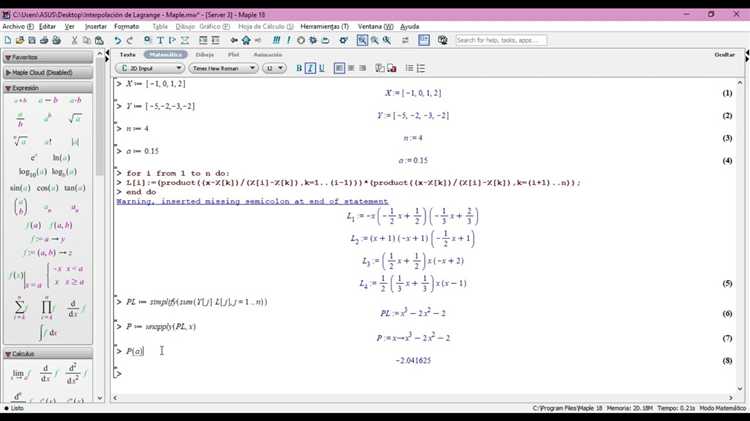
В Maple узлы интерполяции могут задаваться как числовыми значениями, так и символьными выражениями. Для числовых узлов рекомендуется использовать тип данных с плавающей точкой (например, 1.0, 2.5), что обеспечивает точность вычислений и корректную работу встроенных функций интерполяции. При работе с символьными узлами важно явно указывать переменные и сохранять структуру выражений без подстановки числовых значений, чтобы обеспечить возможность аналитического упрощения и дифференцирования полинома Лагранжа.

Для создания массива узлов с числовыми значениями удобно применять функцию Vector или списки, при этом необходимо избегать смешивания типов данных. Символьные узлы задаются списком символов или выражений без преобразования в числовой формат. При построении интерполяционного полинома используйте команду LagrangeInterpolation из пакета PolynomialTools с явно указанными списками узлов и значений функции, чтобы избежать неоднозначностей.

Если узлы имеют символьный вид, например x=-1, 0, 1, убедитесь, что переменная x определена в Maple и не перезаписана числовыми значениями. Для числовых узлов предпочтительно предварительно задать массив с типом float, чтобы исключить ошибки округления. Для анализа точности интерполяции рекомендуется сравнивать числовые результаты с аналитическими выражениями, используя команды evalf и simplify.

В случаях, когда узлы заданы символьными параметрами, полезно применять команду subs для подстановки конкретных числовых значений на этапе проверки построенного полинома. Это позволяет контролировать поведение интерполяционного многочлена и выявлять ошибки в исходных данных.

Автоматизация построения с использованием процедур Maple

Для автоматизации построения полинома Лагранжа в Maple целесообразно создать специализированную процедуру, принимающую на вход массив узловых точек и соответствующих значений функции. Такая процедура должна последовательно вычислять базисные многочлены Лагранжа и формировать итоговый интерполяционный полином.

Рекомендуется использовать встроенную команду mul для эффективного вычисления произведений в базисах, а также функцию expand для раскрытия скобок и упрощения результата. Это повышает читаемость итогового полинома и облегчает последующую работу с ним.

Пример структуры процедуры:

LagPoly := proc(x_values::list, y_values::list, var::name) local n, i, j, L, P; n := nops(x_values); P := 0; for i from 1 to n do L := 1; for j from 1 to n do if j <> i then L := L * (var — x_values[j])/(x_values[i] — x_values[j]); end if; end do; P := P + y_values[i] * L; end do; return expand(P); end proc;

При использовании данной процедуры можно быстро менять наборы точек без переписывания кода, что существенно сокращает время подготовки вычислений и снижает риск ошибок при ручном вводе формул.

Для повышения гибкости рекомендуем предусмотреть в процедуре проверку на уникальность узлов и сопоставимость размеров списков значений. Это обеспечит корректность работы даже при изменении входных данных.

Интеграция таких процедур в скрипты Maple позволяет автоматически генерировать интерполяционные полиномы для задач численного анализа, визуализации и моделирования, что существенно расширяет возможности быстрого прототипирования и анализа.

Вопрос-ответ:

Как в Maple задать набор узлов для построения полинома Лагранжа?

В Maple можно определить узлы интерполяции, создав список пар (x, y), где x — координаты узлов, а y — значения функции в этих точках. Для этого обычно используют структуру данных типа list или массив. Далее на основе этого списка строится интерполяционный полином с помощью встроенных функций или вручную, прописывая формулу Лагранжа.

Какие команды Maple позволяют автоматически получить полином Лагранжа по заданным точкам?

Для вычисления интерполяционного полинома Лагранжа в Maple используют пакет PolynomialTools, где доступна функция Interpolation или LagrangeInterpolation. Эти команды принимают набор точек и возвращают выражение для полинома в символьном виде. Такой подход упрощает процесс и избавляет от необходимости вручную рассчитывать коэффициенты.

Можно ли в Maple построить полином Лагранжа для функций с большим числом узлов, и какова будет точность?

Maple справляется с построением полинома Лагранжа для большого количества точек, однако при увеличении числа узлов могут возникнуть численные трудности из-за особенностей интерполяции, например, появление колебаний (эффект Рунге). Чтобы минимизировать такие ошибки, иногда используют специальные наборы узлов, например, узлы Чебышёва, либо переходят к другим методам аппроксимации.

Как в Maple можно упростить выражение полинома Лагранжа после его построения?

После построения полинома Лагранжа в Maple часто используют функции simplify или expand для приведения выражения к более удобному виду. Команда simplify уменьшает сложность формулы, а expand раскрывает скобки и показывает полином в развернутом виде. Это помогает лучше понять структуру полинома и облегчает последующие вычисления.

Как визуализировать построенный в Maple полином Лагранжа вместе с исходными узлами?

Для визуализации в Maple применяют команду plot, где можно одновременно отобразить график интерполяционного полинома и точки узлов. Например, строится график функции по формуле, а затем с помощью опции pointplot добавляются метки для узлов. Такой подход помогает оценить качество аппроксимации и увидеть, насколько полином соответствует заданным значениям.