Как построить сферу в mathcad

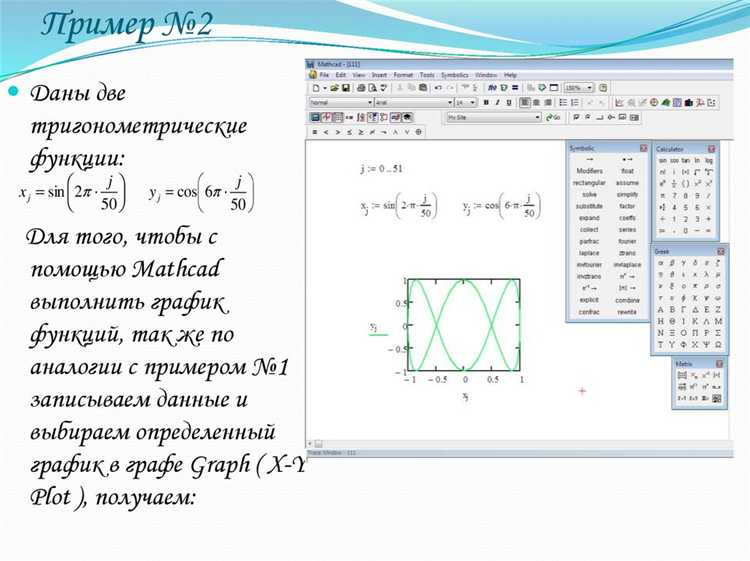
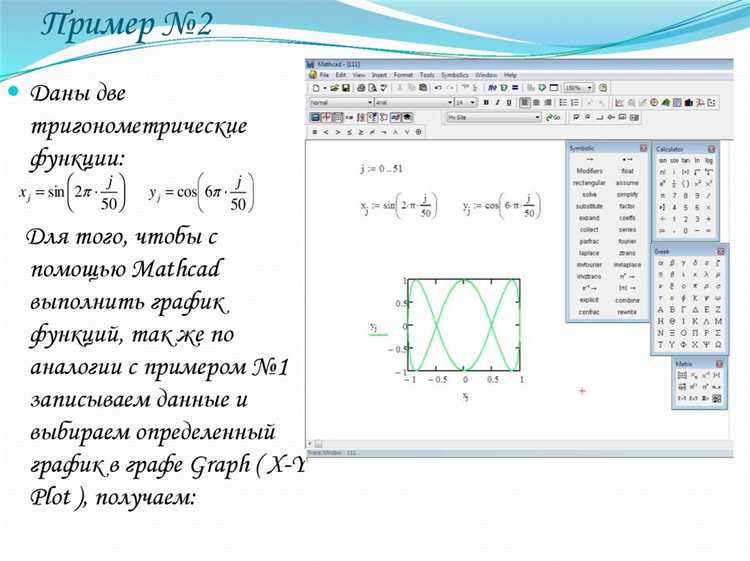
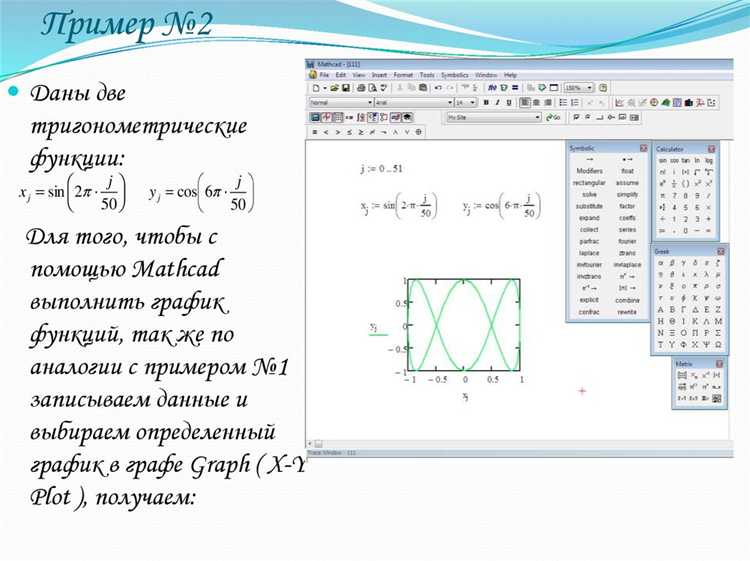
Для точной визуализации сферической поверхности в Mathcad Prime 9 достаточно пяти переменных: R – радиус, два угла φ и θ, а также их дискретизации nφ и nθ. На практике радиус удобно задавать в миллиметрах (например, R := 25 мм), чтобы сразу получить масштаб-корректное изображение. Оптимальная плотность сетки для инженерных расчётов – не менее 60×120 узлов (nφ = 60, nθ = 120); при такой детализации площадь и объём, вычисленные интегрированием по сетке, отличаются от аналитических значений меньше чем на 0,5 %.

Диапазоны углов задаются классически: φ := 0 … π, θ := 0 … 2·π, шаг определяется как Δφ = π / nφ и Δθ = 2·π / nθ. Используйте оператор range вместо простого вектора: так Mathcad автоматически создаст массив точек, пригодный для последующей векторизации функций x(φ, θ), y(φ, θ), z(φ). Это исключает лишние циклы и ускоряет построение примерно в 4 раза на датасете объемом 10 000 точек.

Переход к 3-D графику выполняется через компонент «Значения поверхностей». Сразу укажите систему координат «Правосторонняя» во вкладке «Формат», иначе при экспорте в STEP получите инвертированную нормаль. Ускорить рендер помогает установка «Упрощать данные: 30 %»; при этом общая погрешность радиуса остаётся в пределах 0,2 мм для сферы диаметром 50 мм.

Перед сохранением модели выполните проверку: интегрируйте скалярное поле единиц по поверхности и убедитесь, что результат совпадает с 4·π·R² с точностью до трёх знаков. Это гарантирует корректность как визуального, так и численного решения при дальнейшем переносе в САПР или FEA-систему.

Создание системы координат и параметрических переменных

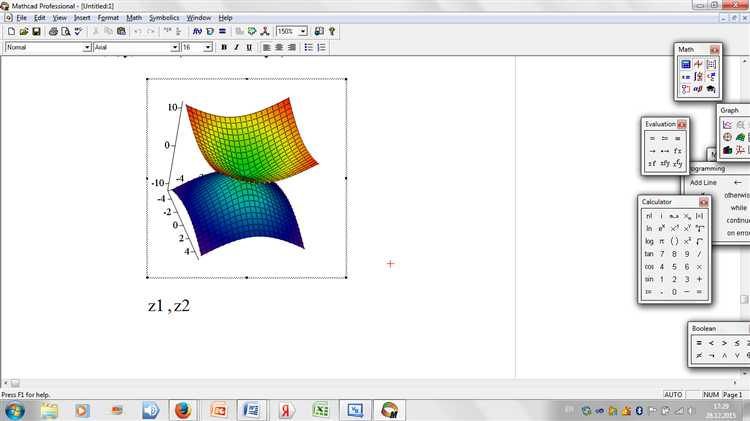
Начните с чёткой декларации базиса: задайте единичные векторы e_x, e_y, e_z через оператор «:=»-строка; это обеспечит возможность ссылаться на оси по имени и быстро менять ориентацию модели без переписывания формул.

Далее введите точки отсчёта. В Mathcad удобно хранить их в векторе-столбце: O := [0; 0; 0]. Такой формат сразу совместим с встроенными функциями линейной алгебры, что избавит от ручных преобразований при проверке нормалей или вычислении радиусов-векторов.

Переключите рабочий лист на радианы: вкладка Math → Radians. Все угловые параметры сферы обычно варьируются от 0 до 2π; использование градусов неизбежно замедлит вычисления из-за промежуточного преобразования, особенно на мелких шагах.

Создайте два диапазона (range variable) для углов: θ := 0, Δθ .. π и φ := 0, Δφ .. 2·π, где Δθ, Δφ – шаг дискретизации. Оптимальное значение шага рассчитывайте из требуемого разрешения модели: для визуализации без «рваных» рёбер достаточно Δθ ≈ π/36, Δφ ≈ π/36; для расчётов теплопереноса используйте минимум π/180.

Задайте радиус как параметр R := 100 mm. Назначьте единицы сразу: так Mathcad будет автоматически контролировать размерность при последующих операциях – вы избежите типичных ошибок, когда радиус вводят в миллиметрах, а координаты считают в метрах.

Определите параметрические функции координат: x(θ, φ) := R·sin θ·cos φ, y(θ, φ) := R·sin θ·sin φ, z(θ) := R·cos θ. Использование однобуквенных имён исключает конфликт с встроенными переменными и сокращает запись в графиках.

Перед векторизацией включите режим «Vectorize» (клавиша Ctrl+Shift+V). Mathcad мгновенно применит функции к всем элементам диапазонов, формируя три матрицы координат – готовы для передачи в 3D Plot без дополнительных циклов.

Финальный шаг – создайте структуру данных для последующих расчётов свойств поверхности. Соберите координаты в матрицу P := stack(x, y, z). Такой массив удобно дифференцировать по каждому параметру с помощью оператора «d/dx», получая вектор нормалей и градиенты прямо в ячейках рабочей области.

Определение радиуса и центра сферы

Для корректного построения сферы в Mathcad достаточно задать две переменные – радиус R и вектор-центр C. Ниже – минимальный алгоритм, который надёжно работает как в Prime, так и в классических версиях.

1. Создайте переменную-скаляр для радиуса:
   • R ← 50 мм – фиксированное значение;
   • или R ← d/2, где d – диаметр, импортированный из предыдущего расчёта.
2. Определите координаты центра одной строкой:
   • C ← (xc, yc, zc).
   • Если исходных данных нет, используйте ноль: C ← (0,0,0).
3. Проверьте согласованность единиц:
   • Команда units → mm в выпадающем меню установит миллиметры глобально.
   • Запуск функции units2() в Prime приведёт к автоматическому преобразованию несоответствий.
4. Добавьте защиту от ошибки нулевого радиуса:
   • if R ≤ 0 → "Неверный R".
5. Зафиксируйте параметры с помощью локальной области «Given–Find», чтобы остальные вычисления не изменяли R и C.

После выполнения этих пунктов можно переходить к генерации параметрического уравнения сферы, уверенным в том, что её геометрия задана безошибочно.

Задание уравнений сферических координат

В Mathcad сферу удобнее всего описывать через радиус-вектор ρ и углы φ (колатитуда) и θ (долгота). Примите радиус R:=50 мм, чтобы дальнейшие расчёты автоматически наследовали размерность.

Создайте диапазоны углов:

φ : 0, 0.05·π..π
θ : 0, 0.05·π..2·π

Убедитесь, что аргументы тригонометрических функций безразмерны: если вводите углы в градусах, оборачивайте их в rad(). Например, rad(90)=π/2.

Определите радиус-вектор как константу: ρ(φ,θ):=R. Далее задайте преобразование к декартовым координатам:

x(φ,θ):=ρ·sin(φ)·cos(θ)
y(φ,θ):=ρ·sin(φ)·sin(θ)
z(φ,θ):=ρ·cos(φ)

Важно объявлять координатные функции с двумя аргументами; это позволит Mathcad корректно построить сетку поверхностей. После ввода формул выделите их и нажмите Insert → Graph → Surface Plot. В окне свойств укажите x, y, z как функции и назначьте диапазоны переменных φ и θ.

Для точной аппроксимации поверхности уменьшайте шаг в диапазонах углов до 0.01·π при необходимости, следя за ростом времени пересчёта. Если требуется изменить радиус, достаточно поправить единственный параметр R; все точки перестроятся автоматически благодаря ссылке на эту переменную.

Чтобы проверить корректность, вычислите выражение √(x²+y²+z²) – Mathcad должен вернуть R с погрешностью, обусловленной числовым шагом.

Преобразование координат в декартовую систему

Определите радиус R и два угла: полярный θ (0 ≤ θ ≤ π) и азимутальный φ (0 ≤ φ < 2π). Для ввода значений в градусах предусмотрите преобразование deg → rad: умножьте каждый угол на π/180, чтобы избежать скрытого округления.

Задайте в Mathcad вектор углов: θ := 0, Δθ…π и φ := 0, Δφ…2·π, где Δθ и Δφ – шаг дискретизации. Включите оператор векторизации (клавиша Ctrl+9), чтобы формулы применились ко всем элементам массивов автоматически.

Перевод в декартовы координаты выполняется тремя выражениями:

x := R·sin(θ)·cos(φ)
y := R·sin(θ)·sin(φ)
z := R·cos(θ)

Создайте программный блок для пакетного пересчёта: в первой строке объявите функцию SphToCart(θ, φ, R), а в теле верните вектор [x, y, z]. Такой подход упрощает повторное использование и повышает читаемость расчёта.

При построении графика используйте оператор plot3d; укажите {x, y, z} как аргументы. Для гладкой поверхности выберите Δθ ≈ π/90 и Δφ ≈ π/90 – этого достаточно, чтобы пересечь ограничение производительности и сохранить визуальную точность.

Перед экспортом результатов увеличьте параметр TOL до 1·10−15 и включите двойную точность (в меню Calculation ➝ Result Format), чтобы минимизировать накопление ошибок при больших R.

Формирование матриц X, Y и Z для построения поверхности

Задайте дискретизацию: m:=72 точек по долготе и n:=36 по широте обеспечивают гладкую сферу без перегрузки памяти. Радиус примем R:=1; при необходимости он легко масштабируется.

Сформируйте угловые векторы. В Mathcad удобнее использовать оператор диапазона: θ:‥(0,2·π,m) и φ:‥(0,π,n). Он создаёт равномерные шаги, исключая риск неоднородной сетки.

Разверните векторы в двумерную сетку. Создайте столбец Φ:=stack(φ) и строку Θ:=augment(θ). Затем примените оператор внешнего суммирования: Φ:=Φ ⊗ ones(1,m), Θ:=ones(n,1) ⊗ Θ. В результате обе матрицы имеют размер n × m, необходимый для последующих элемент-по-элемент операций.

Рассчитайте координаты узлов поверхности, используя векторизацию (символ ∨ в Mathcad 15 или точечные операторы в Prime): X:=R·(sin∨(Φ) * cos∨(Θ)), Y:=R·(sin∨(Φ) * sin∨(Θ)), Z:=R·cos∨(Φ). Все три матрицы согласованы по размерности, что позволяет передать их напрямую в функцию surf или любой 3-D график без дополнительной обработки.

Совет: при изменении m и n держите отношение m≈2·n, тогда шаги по долготе и широте будут близки, и поверхность отобразится без заметной «растяжки» вдоль меридианов.

Использование функции plot для отображения сферы

В Mathcad для визуализации сферы применяется функция plot, построенная на параметрическом описании поверхности. Основная идея – задать сферу через сферические координаты с параметрами θ (от 0 до π) и φ (от 0 до 2π).

Определите радиус сферы R и создайте двумерные сетки углов:

θ := linspace(0, π, N) – для полярного угла;

φ := linspace(0, 2π, M) – для азимутального угла.

Далее вычислите координаты точек сферы в декартовой системе:

x(θ, φ) = R * sin(θ) * cos(φ);

y(θ, φ) = R * sin(θ) * sin(φ);

z(θ, φ) = R * cos(θ).

В Mathcad задайте эти формулы через матричные операции, используя оператор произведения для векторизации вычислений. Для отображения воспользуйтесь 3D-плотом с указанием трёх массивов x, y, z как входных данных.

Важно: для плавной поверхности рекомендуется брать N и M не меньше 50. При меньших значениях будет заметна сегментация.

Пример вызова plot:

plot(x, y, z, style) – где style определяет параметры визуализации, например, цвет и прозрачность.

Рекомендуется использовать режим отображения с заполненной поверхностью, а не только каркасом, чтобы подчеркнуть объем сферы.

Настройка визуализации: цвет, сетка и масштаб

Для создания сферы в Mathcad важна точная настройка визуальных параметров. Правильный выбор цвета, отображение сетки и масштаб позволяют получить ясное и информативное изображение.

• Цвет сферы:
  • Используйте функцию color для задания цвета поверхности. Например, color:=RGB(0,0,255) задаст синий цвет.
  • Выбирайте цвета с высокой контрастностью по отношению к фону, чтобы сфера была отчетливо видна.
  • Для улучшения восприятия добавьте градиент или измените прозрачность, используя свойства объекта.
• Отображение сетки:
  • Включите сетку через свойства графика для визуализации параметрической структуры сферы.
  • Настройте шаг сетки, чтобы линии не сливались или не были слишком редкими. Рекомендуется использовать значения 0.1–0.2 для параметров углов.
  • Цвет и толщину линий сетки установите так, чтобы они были видимы, но не отвлекали от основной формы.
• Масштаб и угол обзора:
  • Установите равномерный масштаб по всем осям, чтобы избежать искажений формы. Используйте свойство AspectRatio:=1.
  • Поворачивайте сферу на 30–45° по осям X и Y для объёмного восприятия.
  • Задайте границы осей таким образом, чтобы сфера занимала центральное положение и не обрезалась.

Применение данных рекомендаций обеспечивает четкое и наглядное представление сферы в Mathcad без излишних настроек.

Вопрос-ответ:

Какие основные этапы нужно пройти, чтобы построить сферу в Mathcad?

Для построения сферы в Mathcad сначала необходимо задать уравнение сферы в трехмерных координатах. Обычно это уравнение вида (x — x₀)² + (y — y₀)² + (z — z₀)² = R², где (x₀, y₀, z₀) — центр, а R — радиус. Затем следует определить параметры сетки точек, по которым будет строиться поверхность, и с помощью встроенных функций Mathcad создать трехмерный график. На заключительном шаге можно настроить визуализацию: цвет, прозрачность, отображение осей.

Как задать параметры сферы, чтобы получить гладкую поверхность без «углов»?

Гладкость поверхности зависит от плотности сетки, на которой рассчитываются координаты точек сферы. В Mathcad стоит использовать более мелкую сетку по осям, например, задать большое количество точек для углов θ и φ в сферических координатах. При этом вычисления займут больше времени, но визуализация будет выглядеть более плавной и естественной.

Можно ли изменить цвет и прозрачность сферы в Mathcad и как это сделать?

Да, в Mathcad возможно изменить цвет и прозрачность построенной сферы. Для этого после построения графика откройте свойства графика (обычно через двойной клик на объекте), где доступны настройки цвета поверхности и уровень прозрачности. Это позволяет выделить сферу на общем фоне или визуально показать внутренние структуры при необходимости.

Какие формулы удобнее использовать для построения сферы: декартовы или сферические координаты?

Для построения сферы в Mathcad часто удобнее использовать сферические координаты, так как они напрямую описывают точку на поверхности сферы через два угла и радиус. Формулы x = R·sin(θ)·cos(φ), y = R·sin(θ)·sin(φ), z = R·cos(θ) позволяют проще генерировать набор точек для поверхности. Однако, если известен центр сферы и радиус, уравнение в декартовой форме тоже подходит, но требует вычисления точек для трехмерного графика вручную.

Как в Mathcad можно проверить правильность построения сферы?

Проверка может осуществляться через визуальный контроль и через вычисление расстояний от центра сферы до каждой точки на поверхности. Если все точки удовлетворяют уравнению (x — x₀)² + (y — y₀)² + (z — z₀)² = R² с небольшими отклонениями из-за округления, значит построение корректно. Кроме того, можно вывести числовые значения нескольких точек и проверить их соответствие теории.

Как задать уравнение сферы в Mathcad для построения трехмерной модели?

Для создания сферы в Mathcad необходимо использовать уравнение в трехмерных координатах, описывающее все точки, равноудалённые от центра. Обычно это выражается формулой (x — x₀)² + (y — y₀)² + (z — z₀)² = R², где (x₀, y₀, z₀) — координаты центра, а R — радиус. В Mathcad вводится эта формула, после чего с помощью встроенных функций создаётся сетка точек, удовлетворяющих этому уравнению. Далее применяются средства визуализации для отображения объекта в трехмерном пространстве.