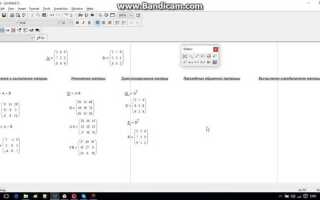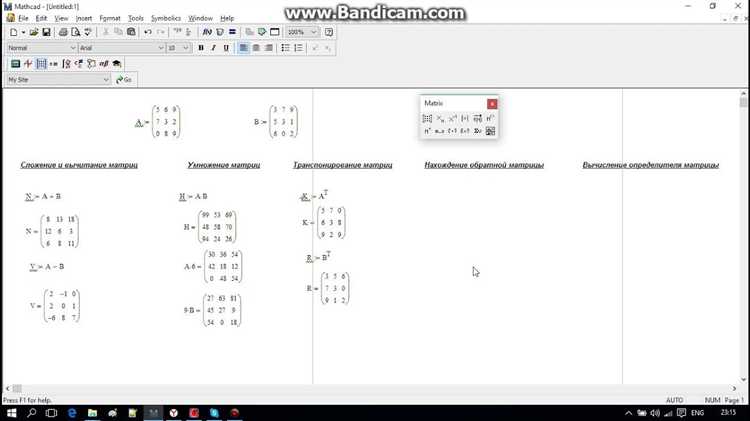
Работа с матрицами в Mathcad основывается на прямом вводе данных и интуитивной визуализации результатов. В отличие от большинства систем компьютерной алгебры, здесь матрицы можно редактировать как двумерные объекты прямо на рабочем листе, задавая как численные значения, так и выражения, зависящие от переменных.
Создание матриц выполняется с помощью клавиши [Ctrl+M] или через вкладку Matrix. Размер задаётся вручную, после чего вводятся элементы. Mathcad поддерживает стандартную индексацию с единицы, что необходимо учитывать при обращении к элементам: M1,1 – это верхний левый элемент.
Для вычислений доступны операции сложения, умножения, транспонирования (transpose(M)) и обращения (inverse(M)). При этом Mathcad автоматически проверяет размерности: попытка перемножить несовместимые матрицы приведёт к ошибке, а обращение сингулярной матрицы – к сообщению о невозможности выполнения операции.
Векторизация выражений осуществляется через оператор vectorize, что позволяет выполнять поэлементные операции без явных циклов. Это особенно полезно при работе с матрицами больших размеров или при параметрических расчётах.
Для символьных преобразований матриц используется оператор → с последующим нажатием [Ctrl+.], что позволяет получить точные аналитические выражения. Это удобно, например, при нахождении собственных значений или решении систем линейных уравнений в символьной форме.
Создание и ввод матриц различных размеров
Для создания матрицы в Mathcad необходимо задать имя переменной, после чего нажать клавишу [Ctrl] + [M]. Появится окно с полями для указания количества строк и столбцов. Например, чтобы создать матрицу 3×2, введите 3 в поле строк и 2 в поле столбцов.
После создания матрицы курсор последовательно перемещается по ячейкам, где можно вводить числовые или символьные значения. Для перехода между элементами используйте клавиши [Tab] и [Shift] + [Tab].
Для изменения размеров уже созданной матрицы выберите её, щёлкнув по имени или структуре, затем используйте правая кнопка мыши → Matrix → Resize Matrix. Mathcad не позволяет напрямую изменять размер матрицы через редактирование элементов – требуется изменить структуру через данную команду.
Создание матрицы нулей или единиц одинакового размера выполняется через встроенные функции: zeros(m, n) создаёт m×n матрицу нулей, ones(m, n) – матрицу из единиц. Использование таких функций удобно при инициализации данных.
Для ввода векторных данных используйте матрицы размером n×1 или 1×n. Однострочный ввод с помощью запятой или точки с запятой невозможен – элементы вносятся только в ячейки матрицы, вызванной через [Ctrl] + [M].
Если необходимо создать символьную матрицу, заполните элементы переменными или выражениями. Mathcad корректно обрабатывает такие структуры при последующих аналитических операциях.
Для больших матриц рекомендуется использовать функции генерации с помощью операторов for в программном блоке или встроенных функций, таких как augment или stack, для объединения меньших матриц в одну.
Операции сложения, вычитания и умножения матриц

В Mathcad сложение и вычитание матриц выполняются поэлементно. Для успешного выполнения операций размеры матриц должны быть идентичными. Например, если заданы матрицы A и B размером 3×3, выражение A + B вернёт новую матрицу, где каждый элемент вычисляется как сумма соответствующих элементов A и B.
Если размеры не совпадают, Mathcad выдаст ошибку. Рекомендуется использовать встроенную функцию rows( ) и cols( ) для проверки совместимости перед выполнением операций. Пример: if rows(A) = rows(B) and cols(A) = cols(B) then A - B.
Умножение в Mathcad различается: для поэлементного умножения используется оператор A * B, но только при совпадающих размерах. Для матричного произведения используется умножение без точки – A B, при этом число столбцов первой матрицы должно совпадать с числом строк второй.
Если требуется транспонировать одну из матриц для обеспечения совместимости, применяется функция transpose( ) или апостроф: A'. Это особенно важно при работе с векторами-строками и векторами-столбцами.
Mathcad отображает результат мгновенно, что позволяет оперативно проверять корректность вычислений. При необходимости автоматизации рекомендуется создавать шаблоны с параметрически заданными размерами.
Поэлементные действия с матрицами
В Mathcad поэлементные операции с матрицами выполняются с использованием оператора «поэлементного действия» – точки (.), поставленной перед арифметическим знаком. Это позволяет выполнять операции между соответствующими элементами двух матриц одинаковой размерности.
.+,.-,.*,./– поэлементное сложение, вычитание, умножение и деление соответственно.- Операции работают только при совпадении размеров матриц. При попытке выполнить поэлементную операцию над матрицами разных размеров возникает ошибка.
- Пример: если заданы
A := [1\ 2; 3\ 4]иB := [5\ 6; 7\ 8], тоA .* Bдаст[5\ 12; 21\ 32].
Для поэлементного возведения в степень используется .^:
A .^ 2– каждый элемент матрицыAвозводится в квадрат.A .^ B– поэлементное возведение элементовAв соответствующие степени изB.
При работе с поэлементными функциями (например, sin, log, exp) перед именем функции необходимо ставить точку:
.sin(A)– применяетсяsinко всем элементам матрицыAиндивидуально..log(B)– логарифм каждого элемента матрицыB.
Рекомендуется:
- Проверять размерность матриц до выполнения поэлементных операций.
- Использовать поэлементные функции вместо циклов – это повышает читаемость и снижает вероятность ошибок.
- Для сложных выражений – комбинировать поэлементные действия и встроенные функции в виде отдельных шагов с промежуточными переменными.
Определение и обращение матриц

В Mathcad матрица создаётся путём ввода элементов в ячейки, автоматически формируемые при использовании клавиши Tab для перехода между столбцами и клавиши Enter для перехода между строками. Размерность матрицы определяется числом заполненных строк и столбцов. Элементы могут быть как числовыми, так и символьными выражениями.
Для присвоения имени матрице используется оператор :=. Например, запись A := с последующим вводом значений создаёт матрицу A. Проверить количество строк и столбцов можно с помощью функций rows(A) и cols(A).
Обращение матрицы выполняется с помощью встроенной функции invert(A) или символа возведения в степень: A^-1. Операция возможна только для квадратных матриц с ненулевым определителем. Попытка обращения вырожденной матрицы вызывает ошибку. Для анализа обратимости используйте функцию det(A): если результат равен нулю, обращение невозможно.
Mathcad автоматически обрабатывает как числовые, так и символьные матрицы. Для символьных выражений рекомендуется использовать символьное преобразование (symbolic), чтобы исключить численные приближения при вычислении обратной матрицы.
Для повышения точности при работе с вещественными матрицами следует избегать операций с близкими по значению строками, чтобы минимизировать численную нестабильность. При необходимости предварительно выполняйте масштабирование или нормализацию строк.
Нахождение собственных значений и векторов

Для нахождения собственных значений и собственных векторов матрицы в Mathcad используется встроенная функция eigenvals(A) – для собственных значений, и eigenvecs(A) – для собственных векторов. Матрица A должна быть квадратной.
Собственные значения возвращаются в виде вектора, где каждый элемент соответствует одному собственному значению матрицы. Собственные векторы возвращаются в виде матрицы, столбцы которой являются нормированными собственными векторами, упорядоченными в соответствии с найденными собственными значениями.
Для корректной работы рекомендуется использовать только численные (не символьные) матрицы с типом элементов float. При работе с комплексными матрицами Mathcad возвращает комплексные собственные значения и векторы.
Пример:
A := [2 1; 1 2 1 2; 2 1] λ := eigenvals(A) V := eigenvecs(A)
Результат:
λ = [3, 1] V = [0.7071 -0.7071 0.7071 0.7071]
Проверка выполняется умножением A·V и сравнением результата с V·diag(λ). Результаты должны совпадать с допустимой погрешностью (обычно до 10⁻¹⁴).
Если требуется символьное представление, необходимо использовать команду symbolic, но она работает только с маломерными матрицами и не всегда гарантирует точный результат при наличии кратных собственных значений.
Рекомендуется избегать плохо обусловленных матриц – это может привести к большим численным ошибкам при вычислении собственных векторов.
Использование встроенных функций для работы с матрицами
Mathcad предоставляет широкий набор встроенных функций, позволяющих выполнять точные и быстрые операции с матрицами. Для получения транспонированной матрицы используется функция transpose(A), где A – исходная матрица. Это удобно при решении систем уравнений и векторных преобразованиях.
Определитель матрицы вычисляется через det(A). При работе с квадратными матрицами это позволяет быстро оценить вырожденность и возможность обращения. Функция inv(A) используется для получения обратной матрицы, если она существует. Попытка обращения сингулярной матрицы вызовет ошибку, что полезно для отладки расчетов.
Для умножения матриц необходимо использовать оператор A·B, который учитывает правила линейной алгебры. Элементное умножение выполняется оператором A * B, что актуально при работе с матрицами одинакового размера.
Поиск собственных значений и собственных векторов реализован через функцию eigenvals(A) и eigenvecs(A). Это особенно важно в задачах анализа устойчивости и динамических систем.
Создание единичной и нулевой матриц выполняется функциями identity(n) и zero(m, n) соответственно. Эти функции ускоряют формирование начальных условий и шаблонов для вычислений.
Для обращения к элементам матрицы используется синтаксис A[i, j], где индексация начинается с нуля. Функция rows(A) возвращает количество строк, cols(A) – столбцов, что полезно при проверке размеров перед операциями.
Функция augment(A, B) объединяет матрицы по горизонтали, stack(A, B) – по вертикали. Это критично при сборке блочных матриц или расширении систем уравнений.
Решение систем линейных уравнений с помощью матриц

Mathcad позволяет эффективно решать системы линейных уравнений вида A·X = B, где A – матрица коэффициентов, X – столбец переменных, B – столбец свободных членов.
- Задайте матрицу коэффициентов A с помощью конструкции:
A := Matrix(n, m), где n – число уравнений, m – число переменных. - Заполните элементы матрицы вручную или с помощью выражений.
- Аналогично создайте вектор B – правую часть системы.
Для получения решения используйте встроенный оператор деления матриц:
X := A⁻¹ · B– вручную через обратную матрицу (только если A невырождена).X := lsolve(A, B)– предпочтительный метод; Mathcad автоматически выбирает оптимальный алгоритм (LU-разложение или метод Гаусса).
Рекомендации:
- Перед применением
A⁻¹проверьте невырожденность матрицы:det(A) ≠ 0. - Используйте
lsolveпри любом размере системы – этот метод устойчив к численным ошибкам и подходит для автоматизации. - Для параметрических решений создавайте символьные матрицы и применяйте оператор
→илиsimplifyдля упрощения.
Для систем с неоднозначным или отсутствующим решением используйте rref(A) – приведённую к ступенчатому виду матрицу для анализа совместности.
Визуализация матричных данных и результат вычислений

Если необходимо визуализировать числовые зависимости внутри матрицы, применяется функция plot. Например, для отображения значений двумерной матрицы Z по координатам X и Y используется график поверхности: plot3D(X, Y, Z). В случае одномерных матриц или векторов рекомендуется применять XY Plot с явным указанием осей.
Для выделения закономерностей и аномалий в матрицах полезно использовать цветовую визуализацию. Mathcad поддерживает цветовые шкалы через опцию Surface Plot в трехмерной графике. При построении графика можно задать цветовую палитру, отражающую диапазон значений. Это особенно эффективно при анализе результатов численного моделирования.
При работе с результатами матричных вычислений (например, умножение, транспонирование, обращение) целесообразно сразу визуализировать результат, чтобы исключить ошибки в индексах или исходных данных. Для этого достаточно ввести имя результирующей матрицы сразу после вычисления и визуально проверить форму и численные значения.
Чтобы улучшить читаемость графиков, рекомендуется настраивать оси, сетку и подписи. Названия переменных можно добавить вручную в свойствах графика. Указание диапазона осей позволяет сосредоточиться на интересующем участке данных.
Также возможно экспортировать визуализированные графики в форматы PNG или JPEG для включения в отчёты. Для этого следует кликнуть правой кнопкой по графику и выбрать пункт «Export Image».
Вопрос-ответ:
Как в Mathcad можно создать и задать матрицу?
В Mathcad матрица создаётся с помощью инструмента для вставки матриц, где можно указать число строк и столбцов. После этого ячейки заполняются значениями или выражениями. Также можно задать матрицу, используя оператор вложенных скобок, например, записав в виде [[1, 2], [3, 4]] — это создаст матрицу 2×2 с указанными элементами.
Какие операции с матрицами поддерживаются в Mathcad и как их выполнять?
Mathcad позволяет выполнять различные операции: сложение и вычитание матриц одинакового размера, умножение матриц с соблюдением правил умножения, транспонирование, вычисление определителя и обратной матрицы. Для умножения используется оператор умножения (*), а транспонирование вызывается через функцию transpose или символ T. Определитель находится через det, а обратная матрица — через inv.
Можно ли в Mathcad вычислять собственные значения и собственные векторы матриц?
Да, Mathcad предоставляет функции для вычисления собственных значений и собственных векторов. Для этого используется функция eig, которая возвращает набор собственных значений и соответствующих собственных векторов для заданной квадратной матрицы. Результаты выводятся в виде вектора и матрицы соответственно, что позволяет анализировать свойства матрицы.
Какие ограничения существуют при работе с большими матрицами в Mathcad?
Работа с очень большими матрицами может замедлить вычисления и увеличить использование оперативной памяти. Mathcad не предназначен для обработки гигантских массивов данных, поэтому при работе с матрицами размером более нескольких тысяч элементов возможны задержки. Кроме того, некоторые функции могут иметь ограничения на размер входных данных или точность вычислений, что стоит учитывать при планировании задач.