Как сделать корень в mathcad

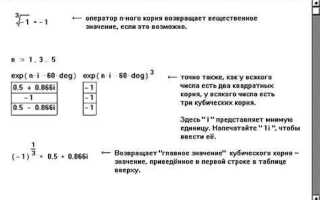
Mathcad предоставляет несколько методов для вычисления корней уравнений, включая численные и аналитические подходы. Ключевым инструментом является встроенная функция root, предназначенная для нахождения корня нелинейного уравнения в заданном интервале. Она требует трех аргументов: уравнение, начальное приближение и переменную. Например, выражение root(x^3 — 5x + 1, x, -2) возвращает значение x, при котором функция обращается в ноль.

Для систем уравнений используется функция Find в сочетании с оператором Given. Этот метод позволяет задать несколько уравнений и получить численное решение при наличии стартовых приближений. Пример: задать систему уравнений через Given, указать уравнения и применить Find(x, y) для получения корней.

В случае необходимости точного аналитического выражения применяется функция solve в символьном режиме. Она возвращает одно или несколько аналитических решений, если таковые существуют. Однако символьные методы работают ограниченно с трансцендентными и более сложными выражениями, поэтому предпочтительнее использовать численные подходы для большинства инженерных задач.

При вычислении корней в Mathcad важно учитывать диапазон значений переменной, чувствительность к начальному приближению и поведение функции. Графическое отображение функции с помощью plot значительно облегчает выбор начальных значений и позволяет избежать ложных корней или сходимости к локальным экстремумам.

Вычисление квадратного корня с использованием встроенной функции sqrt

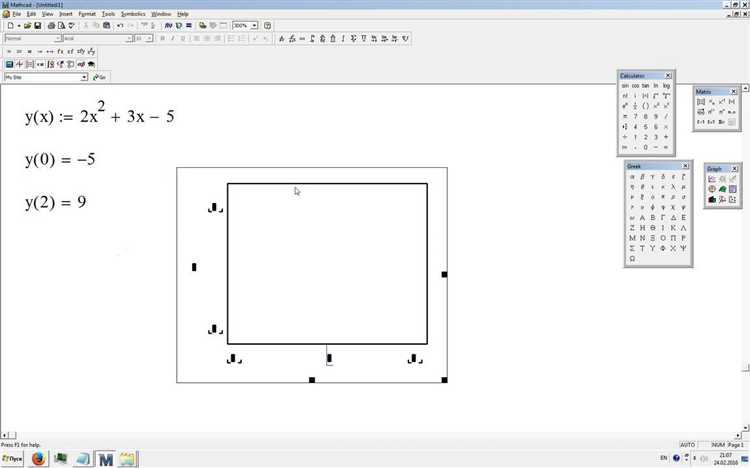
Функция sqrt в Mathcad применяется для нахождения квадратного корня из числа или выражения. Она возвращает положительное значение корня и принимает один аргумент.

• Синтаксис: sqrt(x), где x – неотрицательное число или выражение.
• Пример: sqrt(49) возвращает 7.
• Если аргумент отрицательный, результат будет комплексным числом. Пример: sqrt(-4) возвращает 2i.
• Поддерживается применение к матрицам. В этом случае операция выполняется поэлементно.

1. Введите выражение: выделите рабочую область и напечатайте sqrt(25).
2. Нажмите = или Enter – результат отобразится автоматически.
3. Для выражений: sqrt(a^2 + b^2) – формула используется, например, для вычисления длины вектора.

При работе с переменными важно задать их значения заранее. Пример:

• a := 3
• b := 4
• sqrt(a^2 + b^2) = 5

Функция sqrt не требует подключения дополнительных библиотек. Её использование предпочтительно для повышения читаемости расчетов и упрощения аналитических выражений.

Нахождение корней уравнений с помощью функции root

Функция root в Mathcad применяется для численного поиска корня нелинейного уравнения. Она требует три аргумента: выражение, переменную и начальное приближение. Формат вызова: root(выражение, переменная, начальное_приближение).

Пример: чтобы найти корень уравнения sin(x) - x/2 = 0 вблизи x = 1, используйте:

root(sin(x) - x/2, x, 1)

Результат зависит от выбора начального приближения. При плохом выборе Mathcad может не найти корень. Если предполагается несколько корней, вызывайте root с разными начальными значениями.

Функция работает корректно только при наличии одного корня в окрестности приближения. При наличии разрывов или неоднозначности необходимо предварительный анализ графика функции.

Для параметрических уравнений допустимо использование root внутри программных блоков, где параметры варьируются, а корни рассчитываются итеративно. Пример: нахождение корня уравнения x^2 - a = 0 для различных a:

root(x^2 - a, x, 1)

Если уравнение содержит несколько переменных, остальные следует предварительно определить, чтобы root воспринимал только одну неизвестную.

Функция возвращает числовой результат с точностью, установленной в параметрах документа. Для повышения стабильности желательно избегать уравнений с вертикальными асимптотами или разрывами первого рода.

Вложенное использование root допускается, но усложняет отладку. Рекомендуется пошаговая проверка подынтегральных выражений или ограничение области определения через условные конструкции.

Решение нелинейных уравнений методом Find

Функция Find в Mathcad применяется для численного нахождения корней нелинейных уравнений и систем уравнений. Для корректной работы необходима предварительная инициализация переменных и использование оператора Given.

Объявление переменной осуществляется до блока уравнений, например: x := 1 – это стартовое приближение. Затем используется блок Given, в котором записывается уравнение в виде f(x) = 0.

После блока Given вызывается функция: Find(x). Результатом будет корень уравнения, удовлетворяющий условиям и близкий к начальному приближению.

Если уравнение имеет несколько решений, Find возвращает ближайшее к указанному начальному значению. При плохом выборе начального приближения возможен ошибочный результат или сообщение об ошибке.

Для систем уравнений каждую переменную необходимо инициализировать отдельно, например: x := 1; y := 2. Уравнения в блоке Given записываются построчно, после чего вызывается Find(x, y).

Рекомендуется использовать Find при наличии хороших начальных приближений и когда аналитическое решение невозможно или затруднено. В случаях чувствительности к начальному значению эффективна визуализация функции с помощью графика перед применением метода.

Использование графического способа для визуального поиска корня

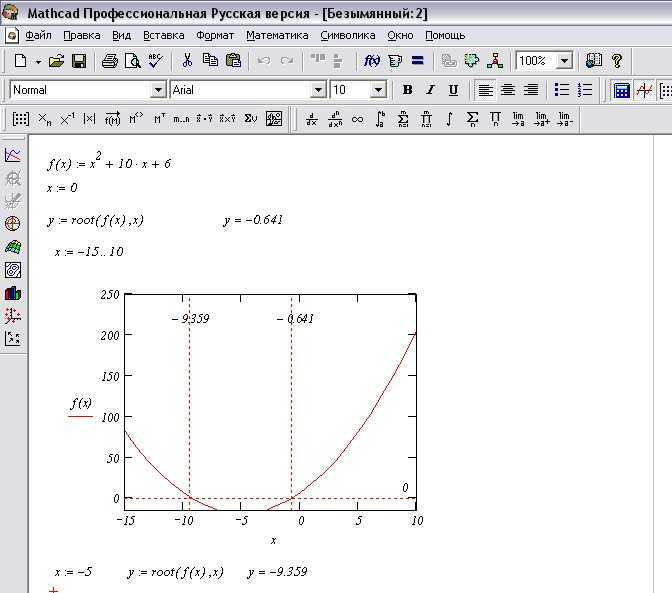
В Mathcad визуальный поиск корня уравнения удобно реализуется через построение графика функции. Для этого необходимо определить диапазон переменной и построить график функции \( f(x) \). Например, при поиске корня уравнения \( f(x) = \cos(x) — x \), сначала задаётся интервал, например: \( x := 0, 0.1..2 \).

Затем функция определяется как: \( f(x) := \cos(x) — x \). Используется встроенный графический модуль: на панели «Построения» выбирается тип «X-Y график» и на оси X наносится переменная \( x \), на оси Y – \( f(x) \). Mathcad автоматически отобразит график функции по заданному интервалу.

Корень визуально определяется как точка пересечения графика функции с осью X. Чтобы уточнить значение, удобно использовать курсор: при наведении на график отображаются координаты. Если точка пересечения не попадает точно на сетку, следует сузить диапазон и уменьшить шаг переменной, например \( x := 0.5, 0.01..0.9 \), чтобы повысить точность визуальной оценки.

Для сложных функций рекомендуется использовать несколько графиков на разных интервалах, чтобы выявить все возможные корни. Также полезно добавить вспомогательную линию \( y = 0 \) для точной ориентации относительно оси X.

Графический способ позволяет быстро определить приближённое значение корня, что особенно полезно на этапе предварительного анализа перед использованием численных методов, таких как функция root.

Построение системы уравнений для поиска нескольких корней

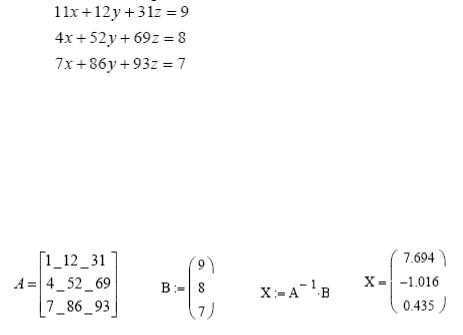
В Mathcad удобно решать задачи с несколькими корнями путём преобразования исходной функции в систему уравнений. Это позволяет задать начальные приближения для каждого корня и использовать встроенную функцию root или оператор solve.

Чтобы найти несколько корней, создайте вектор переменных x := [x₁, x₂, ..., xₙ], где каждая переменная соответствует отдельному корню. Далее сформируйте систему вида:

F(x) := [f(x₁), f(x₂), ..., f(xₙ)]

Добавьте условия для разделения корней, например x₂ - x₁ > ε, чтобы исключить повтор. Эти ограничения можно включить как дополнительные уравнения в систему или задать через ограничивающие функции.

Для численного решения используйте блок Given-Find. Внутри блока укажите систему уравнений и передайте в Find(x) начальные приближения для всех переменных. Например:

Given
f(x₁) = 0
f(x₂) = 0
x₂ - x₁ > 0.5
x := Find(x₁, x₂)

Если требуется найти больше трёх корней, целесообразно использовать циклы с итерационным обновлением начальных условий. Это особенно эффективно при наличии графика функции, по которому можно визуально определить интервалы, содержащие корни.

Для автоматизации поиска нескольких корней полезно применять функцию root(f(x), x, a, b) с параметрами интервала. Повторяя вызов для разных неперекрывающихся отрезков, можно получать все корни в пределах области определения функции.

Важно контролировать шаг интервала и избегать слишком близко расположенных корней, чтобы избежать сходимости к одному и тому же значению. Оптимальный шаг подбирается экспериментально, исходя из поведения функции на графике.

Применение численных методов через функцию Given

Для нахождения корня уравнения методом Ньютона или методом простой итерации рекомендуется использовать конструкцию:

Given(x = initial_guess), f(x) = 0

где initial_guess – начальное приближение, от которого зависит скорость сходимости и успешность поиска корня.

Mathcad автоматически подбирает значение переменной, при котором функция обращается в ноль, используя встроенные численные алгоритмы. Для повышения точности вычислений полезно задавать дополнительное условие ограничения области поиска или указывать начальное приближение максимально близко к предполагаемому корню.

Для сложных функций, где аналитическое выражение корня затруднено, Given позволяет комбинировать несколько уравнений, тем самым реализуя систему, где переменные находятся одновременно. В таких случаях использование Given ускоряет вычисление, снижая необходимость ручного программирования итерационных циклов.

Для контроля результата следует использовать встроенные функции проверки сходимости и оценивать значение функции в найденной точке. При больших отклонениях от нуля требуется изменить начальное приближение или применить другой численный метод.

Оптимально использовать Given для поиска корней уравнений, которые не поддаются простой алгебраической обработке, а также для систем уравнений с несколькими переменными, благодаря удобному синтаксису и интеграции с вычислительным ядром Mathcad.

Анализ ограничений области определения при вычислении корней

При вычислении корней в Mathcad важно учитывать ограничения области определения функций, чтобы избежать некорректных результатов или ошибок. Для корней чётной степени (например, квадратных) выражение под радикалом должно быть неотрицательным. Это значит, что перед вычислением необходимо проверить условие выражение ≥ 0. Если оно нарушается, Mathcad вернёт комплексное число или ошибку.

Для корней нечётной степени таких ограничений нет, поскольку в реальной области функция определена для всех значений аргумента. Однако в случае численного вычисления с приближёнными методами стоит контролировать, чтобы подкоренное выражение не содержало точек разрыва или неопределённостей.

При работе с параметрическими функциями важно анализировать зависимость области определения от параметров. Например, если под корнем содержится выражение вида a*x + b, необходимо обеспечить, чтобы при изменении параметров a и b сохранялось условие неотрицательности для нужного диапазона x.

Рекомендуется использовать встроенные в Mathcad средства проверки условий, такие как логические выражения и функции when, if, чтобы предотвращать попытки вычисления корней вне допустимой области. Это позволяет автоматически исключать значения, при которых вычисления некорректны.

Также важно учитывать особенности вычислительных методов: методы численного решения уравнений и приближённого вычисления корней могут не сработать или дать ошибочные результаты, если стартовые приближения выходят за область определения. В таких случаях целесообразно ограничивать интервал поиска корней явно.

Вопрос-ответ:

Какими способами в Mathcad можно найти корень уравнения?

В Mathcad существует несколько подходов для вычисления корня уравнения. Наиболее распространённый — использование встроенной функции root или root_find, которая позволяет найти значение переменной, при котором выражение становится равным нулю. Также можно применять численные методы, такие как метод Ньютона или метод бисекции, реализованные через собственные вычисления в блоках программирования Mathcad. Выбор способа зависит от вида уравнения и требуемой точности.

Как использовать функцию root в Mathcad для решения нелинейных уравнений?

Функция root в Mathcad используется для вычисления корня уравнения f(x)=0 относительно переменной x. Для этого нужно записать уравнение в виде выражения с переменной и применить root, указав начальное приближение. Например, root(f(x), x, x0) ищет корень функции f(x) около точки x0. Начальное значение играет важную роль — от него зависит, к какому корню сойдётся метод, если их несколько. Функция подходит для уравнений, которые можно задать аналитически и которые непрерывны в окрестности предполагаемого корня.

Можно ли в Mathcad вычислить корень уравнения с несколькими переменными?

Да, в Mathcad возможно найти корень системы уравнений с несколькими переменными, используя функции для решения систем nonlinear уравнений. Для этого применяют функцию root с векторной переменной или используют специальные инструменты для решения систем. Важным условием является задание системы в виде набора уравнений и предоставление начального приближения для всех переменных. Mathcad затем применяет численные методы для одновременного поиска значений переменных, при которых все уравнения обращаются в ноль.

Какие есть ограничения при использовании численных методов для поиска корня в Mathcad?

При применении численных методов в Mathcad нужно учитывать, что результат зависит от выбора начального приближения, свойств функции (например, гладкости и непрерывности) и особенностей алгоритма. Если функция имеет разрывы или несколько корней близко друг к другу, метод может не сойтись или найти не тот корень. Кроме того, для некоторых функций могут возникать проблемы с точностью, если корень кратный или граница области поиска выбрана неверно. В таких случаях рекомендуется проверять результаты и при необходимости корректировать исходные данные.

Как можно автоматизировать процесс поиска корней в Mathcad для серии уравнений?

В Mathcad можно создавать скрипты и использовать циклы для автоматизации вычисления корней множества уравнений. Например, задавая массив функций и применяя к ним функцию root в цикле, можно получить корни всех уравнений автоматически. Такой подход удобен при работе с параметрическими задачами или при необходимости быстро обрабатывать большие наборы уравнений. Важно заранее определить диапазон начальных приближений и условия сходимости для каждого случая, чтобы минимизировать ошибки и ускорить процесс.

Какие методы в Mathcad можно использовать для вычисления квадратного корня числа?

В Mathcad для нахождения квадратного корня применяются несколько способов. Наиболее простой — использование встроенной функции sqrt(x), которая возвращает корень из числа x. Кроме того, можно возвести число в степень 0.5, записав x^(0.5). Еще один вариант — использовать численные методы, например, итерационный алгоритм Ньютона, если нужно получить корень с высокой точностью или для более сложных выражений.