Работа с системой уравнений в Mathcad требует понимания как синтаксиса программного продукта, так и особенностей численного и символьного решения. В Mathcad системы уравнений можно задавать как в виде набора алгебраических выражений, так и через векторы и матрицы. Программа автоматически определяет переменные и применяет встроенные алгоритмы для их вычисления.
Для численного решения необходимо использовать оператор solve блок, обозначаемый ключевым словом Given. После этого указываются все уравнения системы, а также целевые переменные. Завершается блок использованием функции find. Пример: Given, x + y = 5, x — y = 1, find(x, y). Mathcad вернет численные значения переменных при наличии единственного решения.
Символьное решение осуществляется с помощью оператора символического равенства = с нажатием клавиши [Ctrl] + [.] или команды solve. В отличие от численного, этот подход позволяет получить выражения в аналитическом виде. Это полезно при параметрических расчетах или проверке общих свойств системы.
Важно учитывать: переменные должны быть предварительно определены или оставлены неопределенными для корректной работы решателя. Также следует избегать переопределения переменных вне блока Given, чтобы избежать ошибок интерпретации значений.
Как ввести систему линейных уравнений с несколькими переменными
Для ввода системы линейных уравнений в Mathcad необходимо использовать матричный подход. Это позволяет упростить решение и автоматизировать вычисления.
- Создайте вектор-столбец переменных. Например, если система включает переменные x, y и z, введите:
X := [x; y; z]
- Задайте матрицу коэффициентов. Каждый элемент соответствует коэффициенту при соответствующей переменной в уравнении:
A := [[2, -1, 3]; [1, 4, -2]; [0, 5, 1]]
- Определите правую часть системы – вектор свободных членов:
B := [5; 3; 7]
- Формализуйте систему уравнением матричной формы:
A ⋅ X = B
- Для получения решения используйте встроенную функцию:
X := lsolve(A, B)
Функция lsolve находит точное решение, если оно существует. Матрица A должна быть квадратной и невырожденной. Если уравнений больше, чем переменных, используйте genfit или minerr для приближённого решения.
Проверяйте размерность всех векторов и матриц. Mathcad не выполняет автоматическое согласование – ошибки размерности блокируют расчёты.
Использование матричного способа задания системы уравнений
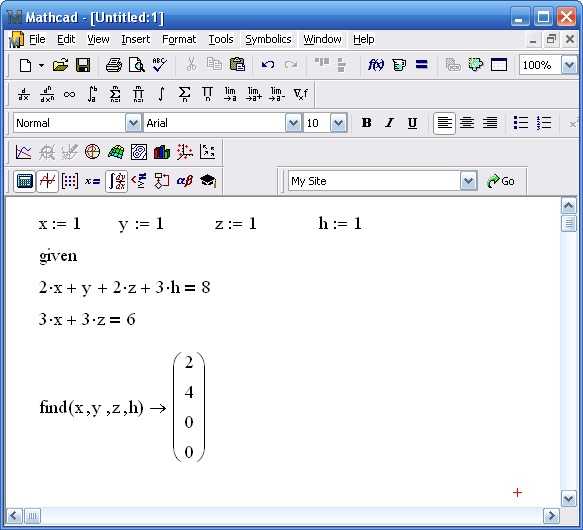
В Mathcad система линейных уравнений может быть представлена в виде матричного уравнения Ax = b, где A – матрица коэффициентов, x – вектор переменных, b – вектор свободных членов. Такой подход особенно эффективен при работе с большим числом уравнений.
Для задания матрицы A необходимо воспользоваться инструментом создания матриц: вставить матрицу нужного размера, например 3×3, и ввести коэффициенты вручную. Все элементы задаются строго по строкам и столбцам, соответствующим структуре системы уравнений.
Вектор переменных x создаётся как столбцовая матрица с символами переменных в том же порядке, в каком они присутствуют в уравнениях. Вектор свободных членов b формируется аналогично: столбец чисел, соответствующих правым частям уравнений.
Для решения используется встроенная функция «solve», которая вызывается следующим образом: x := A⁻¹·b. Mathcad автоматически вычисляет обратную матрицу и производит умножение. Альтернативно, можно использовать оператор обратного деления: x := A\b, что позволяет избежать явного нахождения обратной матрицы и повышает численную устойчивость решения.
При изменении значений в матрице A или вектора b результат решения пересчитывается мгновенно. Это делает матричный способ удобным для анализа параметрических задач и тестирования различных сценариев без переписывания всей системы уравнений.
Как задать начальные приближения для численного решения
В Mathcad при решении систем нелинейных уравнений с помощью функций типа root или find, начальные приближения существенно влияют на сходимость и корректность результата. Их необходимо задавать осознанно, исходя из анализа поведения функции и области определения.
Перед выбором приближений постройте графики функций, входящих в систему. Используйте команды plot или 2D plot для визуальной оценки формы решений. Это позволяет обнаружить интервалы, в которых возможны корни, а также избежать начальных значений вне допустимой области.
Избегайте значений, ведущих к делению на ноль, логарифму отрицательного числа или извлечению корня из отрицательных выражений. Mathcad не сможет обработать такие случаи – решение не сойдётся или приведёт к ошибке.
Если система содержит сильно различающиеся масштабы переменных (например, одна переменная порядка 1, а другая – 10⁶), нормализуйте уравнения или выберите приближения, соответствующие масштабам каждой переменной. Это стабилизирует процесс итераций.
Для многоэкстремальных функций полезно перебирать различные начальные значения, чтобы избежать попадания в локальные, а не глобальные решения. Используйте Given-Find в сочетании с программным сканированием области значений через циклы или функции.
При наличии аналитических оценок или предыдущих вычислений, используйте их для задания начальных точек. Например, при решении динамических систем задайте приближения, близкие к стационарным или известным экспериментальным данным.
Не вводите переменные с равными начальными значениями, если система симметрична – это может привести к вырождению итерационного процесса. Различие хотя бы в одном знаке после запятой может устранить проблему.
После задания приближений проверяйте сходимость, изменяя их в разумных пределах. Это помогает оценить устойчивость решения и выбрать оптимальные значения для повторного использования.
Применение функции solve для нахождения решений системы
Функция solve в Mathcad предназначена для численного решения системы уравнений. Она используется совместно с оператором Given, который указывает Mathcad на необходимость поиска численного решения.
Рассмотрим систему:
x + y = 5
x — y = 1
В Mathcad эта система оформляется следующим образом:
Given x + y = 5 x - y = 1
Далее применяется вызов:
solve(x, y)
Mathcad вернёт вектор-решение с численными значениями переменных. Для доступа к отдельным элементам вектора используйте индексирование: res[0] и res[1], если результат сохранён в переменной res.
Рекомендуется:
- Объявлять переменные до использования в
solve - Избегать переопределения переменных, используемых в других выражениях
- Перед решением убедиться, что система имеет единственное решение (использовать аналитическую проверку либо графическое представление)
Для нелинейных систем рекомендуется указывать начальные приближения, используя операторы присваивания перед Given:
x := 1
y := 1
Given
sin(x) + y = 1
x^2 + y^2 = 4
solve(x, y)
Если решение не найдено, проверьте совместимость уравнений, диапазон начальных приближений и наличие синтаксических ошибок.
Настройка области определения переменных в блоке уравнений

В Mathcad область определения переменных напрямую влияет на корректность решения системы уравнений. Чтобы задать допустимые значения переменных, необходимо использовать оператор диапазона (краткую форму цикла) до начала блока уравнений. Например:
x := 0, 0.1 .. 10
Эта запись определяет область значений x от 0 до 10 с шагом 0.1. Использовать переменные вне их определённого диапазона приведёт к ошибке или некорректному результату.
Для ограничения переменной без явного задания шага следует применять функцию range через массив условий. Например:
0 ≤ x ≤ 5
Внутри блока уравнений переменные, не имеющие области определения, считаются символическими и не участвуют в численном решении. Чтобы исключить неоднозначность, определяйте все переменные заранее, включая параметры с фиксированным значением.
Если переменная должна быть ограничена интервалом, но использоваться только в численном решении, задайте её значение через функцию guess value с диапазоном. Например:
x := 1; x ∈ [0, 5]
Для нелинейных систем важно задавать адекватные начальные приближения. Mathcad использует эти значения для поиска решения методом итераций. В случае отсутствия области определения метод может не сойтись.
Вложенные блоки инициализации переменных не поддерживаются. Определения должны быть расположены строго перед блоком уравнений. Любые попытки изменить область после – игнорируются системой.
При работе с несколькими переменными используйте последовательное определение:
x := 0 .. 5
y := -1 .. 1
Это обеспечит однозначность области поиска решений в многоразмерных задачах. Не задавайте переменные внутри блоков solve block: они не воспринимаются как численные, что приведёт к символьному решению или ошибке.
Работа с системой нелинейных уравнений через функцию root
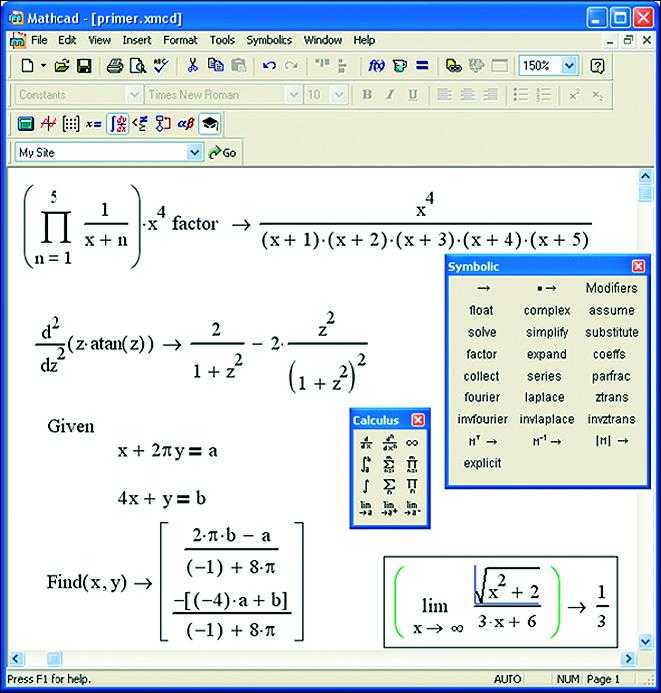
В Mathcad необходимо задать систему в виде вектора:
f(x) = [f₁(x), f₂(x), …, fₙ(x)]
где x – вектор переменных. Затем root применяется так:
x_реш = root(f(x), x_нач),
где x_нач – начальное приближение, важное для сходимости метода.
Рекомендуется использовать вектор начальных приближений с размерностью, соответствующей количеству переменных. Уточнение приближений улучшает точность и сокращает количество итераций. Mathcad автоматически применяет метод Ньютона с численным вычислением Якобиана, поэтому функции должны быть дифференцируемы.
При составлении системы следует избегать выражений, вызывающих деление на ноль или неопределённости в области начального приближения. Для контроля решения рекомендуется дополнительно проверять значения функций в найденной точке – они должны стремиться к нулю с заданной точностью.
Для повышения устойчивости решения полезно разбивать сложные системы на подмножества или использовать ограничение области поиска, изменяя начальные приближения. В случаях, когда root не сходится, стоит пересмотреть формулировку уравнений или использовать более точные начальные приближения.
Отображение и проверка решений с помощью встроенных функций
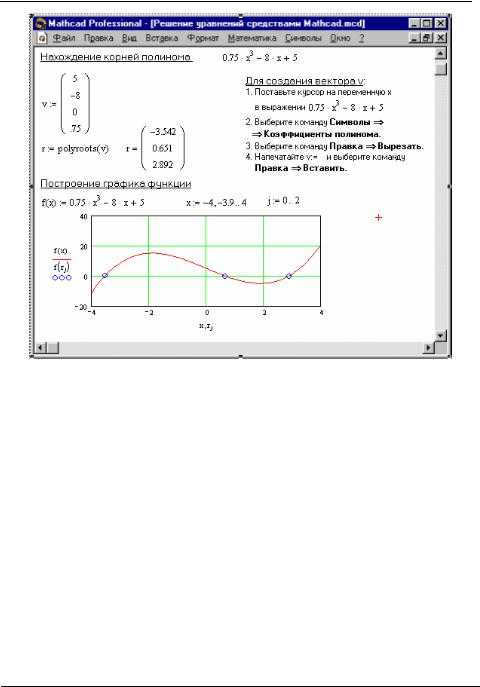
Проверка корректности решений осуществляется подстановкой найденных значений в исходные уравнения. Для этого достаточно подставить решения в левую часть уравнения и сравнить результат с правой частью. Mathcad автоматически вычислит точность и отобразит отклонение.
Для систем с несколькими переменными рекомендуется использовать функцию solve() совместно с операторами сравнения, что позволяет сразу оценить, насколько решения удовлетворяют системе. При численных методах полезно задавать параметры точности и максимальное число итераций для стабильности результата.
Графическое представление решений выполняется с помощью функций построения графиков, таких как plot() или contour(), что позволяет визуально оценить пересечение решений в координатных плоскостях. При этом важно корректно задать диапазоны переменных, чтобы избежать искажения изображения.
Использование встроенных функций Mathcad для отображения и проверки значительно ускоряет процесс анализа и снижает вероятность ошибок, особенно при сложных системах уравнений с нелинейными компонентами.
Диагностика ошибок при решении системы уравнений
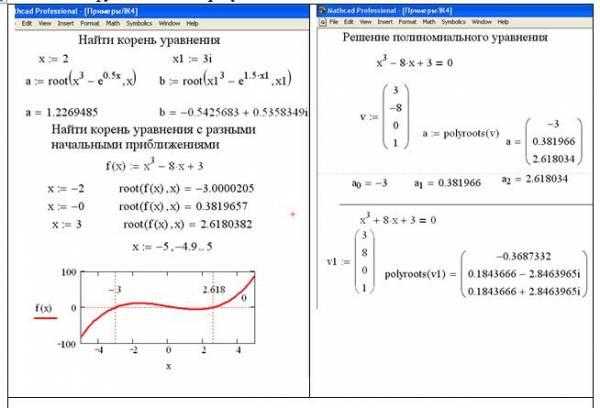
Ошибки при решении системы уравнений в Mathcad часто связаны с некорректной постановкой задачи или неверным вводом данных. Для эффективной диагностики необходимо использовать пошаговый анализ результатов и проверку исходных условий.
- Проверка размерностей переменных и матриц. Несоответствие размеров векторов и матриц вызывает ошибки вычислений. Обязательно сверяйте размерности перед использованием операторов умножения и сложения.
- Контроль исходных данных. Убедитесь, что коэффициенты и константы введены корректно. Часто ошибки связаны с неправильным форматом чисел или пропущенными знаками.
- Использование встроенных функций Mathcad для проверки решения. Например, функция
root()возвращает статус решения – если статус отрицательный, стоит проверить условия задачи. - Анализ остатка уравнений. Подставьте найденное решение обратно в систему, вычислите разности левой и правой частей. Если остатки превышают допустимую погрешность, решение некорректно.
- Проверка сходимости итерационных методов. При решении нелинейных систем важно контролировать количество итераций и изменения значений переменных. Резкие скачки или отсутствие улучшений указывают на нестабильность.
- Изучение сообщения об ошибке Mathcad. Текст ошибки часто содержит информацию о причине сбоя – несогласованности уравнений, делении на ноль, переполнении и пр.
Систематический подход к диагностике ошибок включает:
- Проверку корректности математической модели и ее адекватности задаче.
- Тестирование системы на упрощённых вариантах с известными решениями.
- Обращение к справочной документации Mathcad по специфике функций решения систем уравнений.
Внимательное выполнение этих рекомендаций позволяет минимизировать ошибки и повысить точность вычислений при работе с системами уравнений в Mathcad.
Вопрос-ответ:
Как в Mathcad правильно задать систему уравнений с несколькими переменными?
Для создания системы уравнений в Mathcad нужно записать каждое уравнение отдельно и объединить их в вектор или использовать оператор системы. Обычно уравнения записываются через знак равенства, а затем применяется функция решения, например, root или solve. Важно, чтобы количество уравнений соответствовало количеству неизвестных, и переменные были обозначены одинаково во всех уравнениях.
Можно ли в Mathcad решать нелинейные системы уравнений? Какие особенности при этом нужно учитывать?
Да, Mathcad позволяет решать нелинейные системы. При работе с такими системами важно правильно задать начальные приближения для поиска корней, так как решение может зависеть от них. Кроме того, функции должны быть непрерывными и дифференцируемыми в области поиска решения, иначе алгоритм может не сойтись. В Mathcad для таких задач часто используют функцию root, которая ищет корни методом Ньютона или другим численным методом.
Как отобразить результат решения системы уравнений в виде таблицы или списка в Mathcad?
Чтобы показать результаты в таблице, можно создать вектор или матрицу, куда будут помещены значения всех переменных после решения. В Mathcad достаточно записать переменные в виде массива и вывести его на лист. Для создания таблицы с заголовками можно использовать текстовые области рядом с числовыми значениями, формируя таким образом удобный для восприятия вид.
Что делать, если Mathcad не может найти решение системы уравнений?
Если Mathcad не находит решение, стоит проверить корректность введённых уравнений и переменных. Иногда проблема связана с отсутствием начальных значений или неправильным форматом записи функций. Рекомендуется упростить систему, проверить каждое уравнение по отдельности и попробовать задать разные начальные приближения. Также можно попробовать изменить численные параметры решения, если это возможно, или разбить систему на более простые части для последовательного решения.