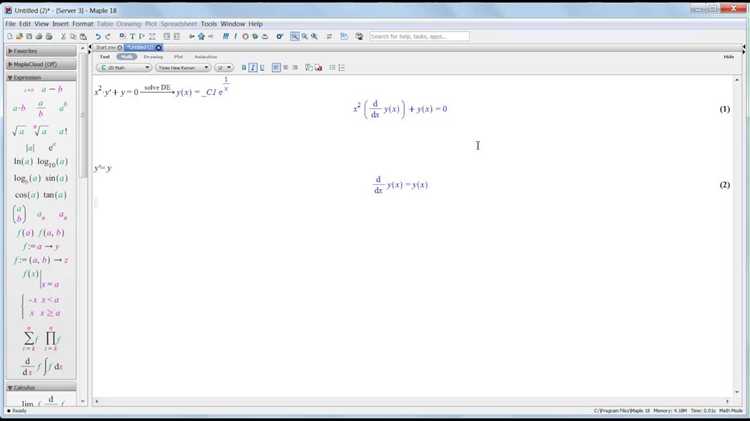
Для решения обыкновенных дифференциальных уравнений используется команда dsolve. Например, вызов dsolve(diff(y(x), x) = y(x)^2, y(x)) возвращает общее решение уравнения первого порядка. При необходимости получения численного решения применяется ключ numeric: dsolve({уравнение, начальные условия}, numeric), что позволяет интегрировать уравнение в заданном интервале и строить графики траекторий с помощью odeplot.
Maple также поддерживает работу с дифференциальными уравнениями в частных производных. Команда pdsolve позволяет решать уравнения с двумя и более независимыми переменными. Например, уравнение теплопроводности diff(u(x,t),t) = diff(u(x,t),x$2) решается с указанием граничных и начальных условий, что позволяет получать точные аналитические выражения для моделируемых процессов.
Для повышения эффективности вычислений рекомендуется предварительно упрощать выражения с помощью simplify и использовать пакет DEtools, включающий функции для классификации уравнений, нахождения интегрирующих множителей и преобразований уравнений в каноническую форму. Эти инструменты особенно полезны при работе со сложными нелинейными уравнениями, где прямое решение может быть недоступно.
Пошаговое решение обыкновенных дифференциальных уравнений первого порядка
Для точного решения обыкновенных дифференциальных уравнений первого порядка в Maple требуется последовательное выполнение следующих действий:
- Запустите Maple и создайте новый документ.
- Задайте уравнение. Например:
ode := diff(y(x), x) = x*y(x);
- Вызовите команду
dsolveдля получения общего решения:dsolve(ode, y(x));
Это вернёт решение вида
y(x) = C*exp(1/2*x^2). - Если требуется найти частное решение, задайте начальное условие:
ode_ic := {diff(y(x), x) = x*y(x), y(0) = 2};dsolve(ode_ic, y(x));
- Если уравнение не приводится к стандартному виду, предварительно преобразуйте его:
ode := (x^2 + 1)*diff(y(x), x) + x*y(x) = sin(x);
ode_solved := dsolve(ode, y(x));
- Проверка решения:
ode := diff(y(x), x) = x*y(x);
sol := dsolve(ode, y(x));
simplify(eval(ode, sol));
Если результат – тождество, решение корректно.
Student[ODEs][SolveSteps](diff(y(x), x) = x*y(x), y(x));
Команда отобразит промежуточные преобразования, включая интегрирование и логарифмирование.
Используйте пакет Student[ODEs] для анализа устойчивости и визуализации, например:
DEplot– фазовые портреты;DEplot(y' = f(x,y), y(x), x = a..b, y = c..d)– направление поля решений.
Использование команды dsolve для получения аналитического решения
Команда dsolve в Maple применяется для нахождения аналитических решений обыкновенных дифференциальных уравнений (ОДУ). Синтаксис: dsolve(уравнение, переменная). Для систем уравнений используется список: dsolve({уравнения}, {переменные}).
Пример: dsolve(diff(y(x), x) = y(x), y(x)) вернёт общее решение y(x) = _C1*exp(x). Константа интегрирования обозначается автоматически через _C1, _C2 и т.д.
Для получения частного решения с начальными условиями необходимо добавить их в вызов: dsolve({diff(y(x), x) = y(x), y(0) = 1}, y(x)). Результат: y(x) = exp(x).
Для решения второго порядка: dsolve(diff(y(x), x, x) - y(x) = 0, y(x)). Maple вернёт: y(x) = _C1*exp(x) + _C2*exp(-x).
Чтобы получить решение в виде выражения без присваивания, используйте параметр numeric только при необходимости численного решения, иначе решение будет символьным по умолчанию.
Если требуется решение в неявной форме, используйте опцию implicit: dsolve(уравнение, переменная, implicit). Это полезно при невозможности выразить переменную явно.
При решении систем рекомендуется явно указывать зависимости переменных, например: dsolve({diff(x(t), t) = y(t), diff(y(t), t) = -x(t)}, {x(t), y(t)}). Это позволяет Maple корректно интерпретировать структуру системы.
Команда dsolve поддерживает линейные и нелинейные уравнения. Для сложных случаев можно комбинировать её с simplify и expand для упрощения результата.
Решение систем дифференциальных уравнений с помощью Maple
Для решения систем дифференциальных уравнений в Maple используется команда dsolve с аргументом в виде списка уравнений и переменных. При решении необходимо явно указать все функции и переменные, входящие в систему.
Пример системы:
sys := [diff(x(t), t) = x(t) + y(t), diff(y(t), t) = -x(t) + y(t)];
dsolve(sys, [x(t), y(t)]);
Для численного решения добавляется опция numeric:
sol := dsolve(sys, [x(t), y(t)], numeric);
Для задания начальных условий система уравнений дополняется уравнениями вида x(0)=a, y(0)=b:
sys_ic := [diff(x(t), t) = x(t) + y(t), diff(y(t), t) = -x(t) + y(t), x(0) = 1, y(0) = 0];
sol := dsolve(sys_ic, [x(t), y(t)], numeric);
Для визуализации траектории решения применяется команда odeplot из пакета plots:
with(plots):
odeplot(sol, [x(t), y(t)], t = 0 .. 10);
При работе с жёсткими системами рекомендуется использовать метод Розенброка или метод обратной дифференцировки, указываемый через опцию method. Пример:
dsolve(sys_ic, [x(t), y(t)], numeric, method = stiff);
Для систем высокого порядка функции необходимо представить в виде систем первого порядка. Maple предоставляет команду convert для преобразования уравнений ко встроенному формату:
convert(ODE, DAE);
Проверка корректности результатов возможна с помощью подстановки решения в исходную систему с использованием команды subs и simplify.
Численные методы решения ОДУ в среде Maple

Для численного решения обыкновенных дифференциальных уравнений в Maple применяется функция dsolve с параметром numeric. Она позволяет получить приближённое решение задачи Коши при наличии начальных условий. Вызов выполняется в формате: dsolve({уравнение, начальные_условия}, numeric).
Maple поддерживает несколько численных алгоритмов, включая метод Рунге-Кутты 4-го порядка (method = rk4), адаптивный метод Каши-Фегеля (method = rkf45) и метод Бюлира (method = gear) для жестких систем. Выбор метода задается явно через опцию method внутри вызова dsolve.
Для доступа к значениям численного решения используется возвращаемая процедура. Например: sol := dsolve(..., numeric), затем sol(0.5) возвращает значение функции при t = 0.5. Для получения значений всех переменных следует обращаться через запись sol(t)[i], где i – номер переменной.
Для анализа поведения решения рекомендуется использовать odeplot из пакета plots. Например, odeplot(sol, [t, y(t)], t = 0 .. 10) визуализирует траекторию переменной y на заданном интервале. Можно строить фазовые портреты или графики нескольких переменных одновременно.
При решении жестких систем целесообразно указывать метод gear, так как стандартные явные методы теряют устойчивость. Также рекомендуется установить малый шаг интегрирования или использовать abserr и relerr для контроля точности.
Для пакетной обработки системы уравнений с параметрами следует использовать цикл и переопределение уравнений с последующим численным решением. Это позволяет исследовать устойчивость, бифуркации и зависимости от параметров без ручного вмешательства.
Построение графиков решений дифференциальных уравнений

В Maple визуализация решений дифференциальных уравнений осуществляется с помощью команды DEplot из пакета plots. Для начала необходимо загрузить пакет:
with(plots):Для построения графика решения ОДУ, заданного уравнением, например diff(y(x), x) = -2*y(x), используйте следующий синтаксис:
DEplot(diff(y(x), x) = -2*y(x), y(x), x = 0..5, y = 0..1, [[y(0) = 1]]);Если необходимо отобразить несколько траекторий при разных начальных условиях:
DEplot(diff(y(x), x) = -2*y(x), y(x), x = 0..5, y = 0..1, [[y(0) = 1], [y(0) = 0.5], [y(0) = 0.2]]);Для систем уравнений требуется использование списка дифференциальных уравнений и соответствующих переменных. Например, система:
sys := [diff(x(t), t) = y(t), diff(y(t), t) = -x(t)];График фазового портрета строится следующим образом:
DEplot(sys, [x(t), y(t)], t = 0..10, [[x(0) = 1, y(0) = 0], [x(0) = 0, y(0) = 1]], scene = [x(t), y(t)]);Для численного решения и последующего построения графика используйте dsolve с опцией numeric:
sol := dsolve({diff(y(x), x) = -2*y(x), y(0) = 1}, y(x), numeric):Затем визуализируйте результат с помощью odeplot:
odeplot(sol, [x, y(x)], 0..5);Если требуется график нескольких переменных системы:
sol := dsolve({diff(x(t), t) = y(t), diff(y(t), t) = -x(t), x(0) = 1, y(0) = 0}, numeric):odeplot(sol, [[t, x(t)], [t, y(t)]], 0..10);Для управления внешним видом графиков используйте параметры: color, thickness, title, legend. Например:
odeplot(sol, [t, x(t)], 0..10, color = red, thickness = 2, title = "x(t)");Работа с начально-краевыми задачами в Maple
В Maple начально-краевые задачи (НКЗ) решаются с помощью пакета DEtools и команды dsolve с опцией bc для задания граничных условий. Основной формат вызова выглядит так: dsolve({уравнение, условия}, y(x), type = numeric). Для численных методов обязательно указывать type = numeric.
Граничные условия задаются в виде уравнений, например, y(0)=1 и y(1)=0. Для производных граничные условия оформляются как D(y)(0)=5. Несколько условий вводятся через множество фигурных скобок.
Для повышения точности решения можно использовать параметры метода численного интегрирования: abserr (абсолютная погрешность), relerr (относительная погрешность), maxmesh (максимальное число узлов сетки). Пример: dsolve({...}, y(x), numeric, abserr=1e-8, relerr=1e-6, maxmesh=500).
Если НКЗ включает сложные дифференциальные уравнения второго порядка, перед численным решением необходимо привести уравнение к системе первого порядка. Maple автоматически это делает, но пользователь может явно задать систему для лучшего контроля.
Для визуализации решения удобно использовать встроенную функцию plots[odeplot], которая принимает численное решение и строит график с необходимым интервалом. Это позволяет быстро оценить поведение функции и проверить корректность заданных условий.
При работе с задачами на отрезках с разрывами параметров следует разбивать задачу на несколько НКЗ и решать по частям, используя результаты одной части как начальные условия для следующей. Такой подход обеспечивает стабильность и точность.
Для сложных граничных условий, например, с зависимостью от производных разного порядка, рекомендуется использовать параметризацию условий через вспомогательные переменные, что позволяет избежать неоднозначностей при интерпретации Maple.
Применение уравнений с частными производными и их решение в Maple
Уравнения с частными производными (УЧП) моделируют процессы в механике, физике, химии и инженерии: теплообмен, волновые явления, диффузия. Maple предоставляет инструменты для аналитического и численного решения таких уравнений, включая методы разделения переменных, преобразования Фурье, Лапласа и вариационные подходы.
Для решения линейных УЧП в Maple используют пакет PDESolve. Команда pdsolve позволяет получить общее или частное решение уравнения с заданными начальными или граничными условиями. Например, для задачи теплопроводности pdsolve(diff(u(t,x),t) = diff(u(t,x),x,x), u(t,x), HINT = 'separation') автоматически выделит переменные и выведет решение в разложении по собственным функциям.
Для более сложных задач с нелинейными или вариационными уравнениями Maple позволяет задавать условия через boundary conditions и использовать численные методы, такие как конечные разности или элементы, через интерфейс pdsolve/numeric. Это обеспечивает построение приближенных решений при отсутствии аналитических формул.
При работе с УЧП важен правильный выбор метода в зависимости от задачи: для стационарных уравнений – разделение переменных и собственные функции, для временных – численные интеграторы. Maple позволяет проверять устойчивость решений и визуализировать результаты, что помогает анализировать физическую интерпретацию.
Рекомендуется перед решением проводить упрощение уравнения с помощью встроенных функций Maple – simplify и convert – для приведения выражений к удобному виду. Автоматическая проверка граничных условий с помощью опции check=true в pdsolve повышает надежность результата.
Использование Maple для решения УЧП сокращает время моделирования и повышает точность за счет интеграции аналитических и численных методов в одной среде, что особенно важно для комплексных инженерных и научных задач.
Автоматизация решений с использованием Maple-процедур
Maple-процедуры позволяют существенно ускорить и упростить процесс решения дифференциальных уравнений за счёт многократного использования и параметризации алгоритмов. Для эффективной автоматизации необходимо следовать следующим рекомендациям:
- Определите шаблон решения для классов уравнений (например, линейные, с разделяющимися переменными, уравнения Бернулли) и оформите его в виде процедуры с параметрами.
- Используйте встроенные команды Maple, такие как
dsolve, в сочетании с управляющими конструкциями (if,for,while), чтобы реализовать логику выбора метода решения в зависимости от формы уравнения. - Включайте в процедуру обработку граничных и начальных условий, чтобы сразу получать частные решения, что исключит необходимость дополнительных вызовов.
- Тестируйте процедуры на наборах типовых уравнений для выявления и устранения ошибок, а также для оценки производительности.
Пример упрощённой процедуры автоматического решения ОДУ первого порядка:
SolveODE := proc(ode, iv)
local sol;
sol := dsolve({ode, iv});
return sol;
end proc;
Данная структура может быть расширена за счёт добавления анализа уравнения и выбора оптимального метода, что повысит универсальность.
- Для более сложных систем рекомендуется использовать рекурсивные процедуры, позволяющие делить задачу на подзадачи и обрабатывать их последовательно.
- Использование Maple-процедур улучшает воспроизводимость результатов и минимизирует человеческий фактор при решении большого объёма уравнений.
- Интеграция процедур с внешними данными и пакетами Maple (например, LinearAlgebra) расширяет возможности по автоматизации анализа и построению решений.
Вопрос-ответ:
Какие типы дифференциальных уравнений можно решать с помощью Maple?
В Maple доступны инструменты для работы с различными типами дифференциальных уравнений, включая обыкновенные дифференциальные уравнения (ОДУ) первого и высших порядков, системы ОДУ, а также уравнения с частными производными (УЧП). Программа поддерживает как аналитические методы решения, так и численные, что позволяет справляться с уравнениями, не имеющими простых точных решений.
Как в Maple задать начальные или граничные условия при решении дифференциальных уравнений?
Для задания начальных или граничных условий в Maple при решении дифференциальных уравнений нужно указать эти условия в качестве дополнительных уравнений вместе с основным уравнением или системой. Например, при использовании функции dsolve можно добавить список условий в квадратных скобках. Это позволяет получить частное решение, удовлетворяющее заданным ограничениям.
Можно ли в Maple получить численное решение, если аналитическое решение дифференциального уравнения невозможно?
Да, Maple предоставляет возможность получать численные решения с помощью встроенных методов, таких как Runge-Kutta и других алгоритмов численного интегрирования. Для этого в функции dsolve используется опция numeric=true, что позволяет получить приближенное решение в виде числовых значений функции на заданном интервале.
Какие команды в Maple помогают визуализировать решения дифференциальных уравнений?
Для построения графиков решений в Maple применяются стандартные функции визуализации, такие как plot для однопараметрических функций и odeplot из пакета DEtools для численных решений дифференциальных уравнений. Эти инструменты позволяют наглядно увидеть поведение решения на выбранном диапазоне переменных.
Как в Maple решить систему нелинейных дифференциальных уравнений?
Для решения систем нелинейных дифференциальных уравнений в Maple можно использовать функцию dsolve, передавая ей список уравнений системы. Если аналитическое решение недоступно, возможно применение численных методов с опцией numeric=true. Важно корректно задать начальные условия для каждого уравнения, чтобы обеспечить точность вычислений.
Какие методы решения дифференциальных уравнений доступны в Maple и как выбрать подходящий для конкретной задачи?
В Maple представлены различные способы решения дифференциальных уравнений, включая аналитические методы, такие как метод разделения переменных, метод вариации постоянных, использование характеристик для уравнений в частных производных, а также численные методы, например, метод Эйлера и Рунге-Кутты. Выбор подхода зависит от типа уравнения и целей пользователя: если требуется точное решение и уравнение допускает его, стоит применять аналитические методы. В случаях, когда аналитическое выражение сложно или невозможно получить, применяют численные алгоритмы. Maple предоставляет команды вроде dsolve для аналитических решений и numeric для численного решения, что позволяет гибко работать с различными типами задач.