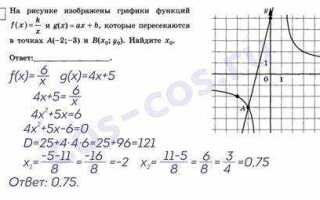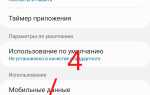
В Mathcad определение точки пересечения двух функций начинается с задания их аналитических выражений. Например, для функций f(x) = sin(x) + 0.5 и g(x) = 0.2·x необходимо ввести их в рабочую область и присвоить переменным. Убедитесь, что диапазон аргумента задан достаточно широко – рекомендуем от x = –10 до x = 10, чтобы захватить все возможные пересечения.
Далее воспользуйтесь конструкцией решателя: введите блок уравнений, где первым уравнением будет f(x) – g(x) = 0, а вторым – условие начального приближения guess := 1 (или другое, подходящее для ваших функций). Mathcad автоматически определит значение x, при котором разность обращается в ноль. После вычисления получите численное значение точки пересечения с точностью до десятитысячных.
Для визуальной проверки отобразите оба графика на одном участке. Добавьте зависимости plot1 := plot(f(x), x, x_min, x_max) и plot2 := plot(g(x), x, x_min, x_max), затем объедините их через оператор «,». Расположение точки пересечения можно отметить маркером: marker := point(x_intersect, f(x_intersect)). Такая наглядность позволяет сразу увидеть, корректно ли найдено пересечение.
При работе с более сложными функциями – например, с полиномами высокой степени или кусочными графиками – рекомендуем перед использованием решателя провести предварительный анализ: понизить шаг дискретизации графиков (Δx = 0.01) и посмотреть области, где разница меняет знак. Это позволит задать несколько начальных приближений и найти все пересечения без пропусков.
Задание функций через математические выражения
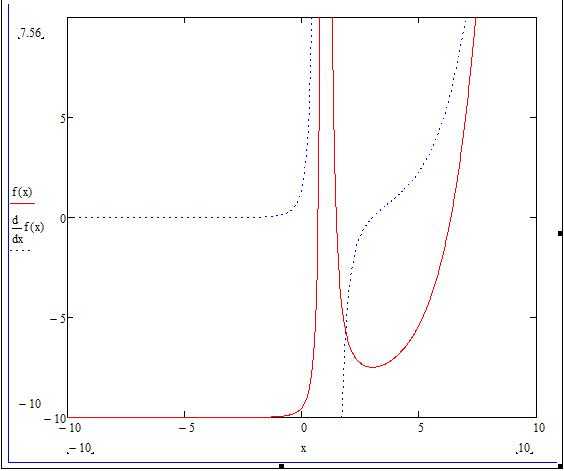
В Mathcad функция задаётся посредством оператора присваивания «:=». В строке ввода необходимо ввести имя функции, затем круглые скобки с аргументами и саму формулу. Например, для квадратичной функции введите f(x):=2·x^2–3·x+5. Mathcad автоматически распознаёт символы умножения, возведения в степень и знаки операций.
Для функций нескольких переменных используйте несколько аргументов: g(x,y):=sin(x)·exp(y/2). Убедитесь, что имена переменных не совпадают с встроенными константами (π, e), иначе система выдаст ошибку. При вводе дробей рекомендуется применять символ «/», например h(t):=(t^3–1)/(t+1), вместо ручного расположения числителя и знаменателя.
При сложных выражениях включайте промежуточные переменные. Например, для функции k(θ)=ln(1+cos(θ)) можно ввести u:=1+cos(θ), затем k(θ):=ln(u). Это повышает читаемость и упрощает отладку.
Используйте встроенные шаблоны функций: в панели Functions доступны тригонометрические, экспоненциальные, логарифмические и специальные функции. При вводе достаточно начать набирать название, и Mathcad предложит автозаполнение.
Чтобы проверить корректность формулы, создайте в калькуляторе точечную проверку: введите f(2) рядом с определением и убедитесь, что результат соответствует ожидаемому значению. Для визуального контроля постройте график функции через инструмент Insert → Graph → X-Y Plot, указав область определения вручную.
Построение графиков функций на одном поле
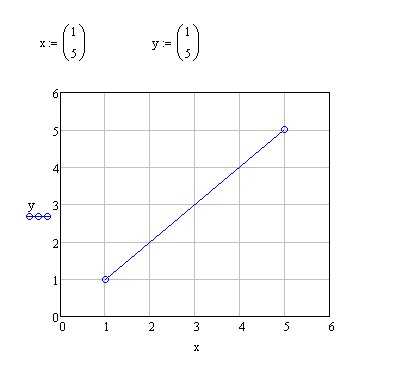
В Mathcad диапазон осей определяется настройками переменных Xmin, Xmax, Ymin и Ymax. Для одновременного отображения нескольких функций задайте одинаковый интервал X, например X:=0,1…10, и через панель свойств графика укажите Ymin=–5, Ymax=15.
Добавьте первый график: выделите выражение f(x)=2·sin(x)+3, щёлкните «График XY» и перетащите f(X) в поле Y. Повторите для g(x)=0,5·X²–4, перетащив g(X) в то же поле Y; цвет линии для второго графика задаётся в параметрах «Стили кривых».
Для точного сравнения функций включите сетку: в свойствах графика отметьте «Показывать сетку», задайте шаг сетки по X=1, по Y=2. Это позволит видеть пересечения в целых координатах.
Чтобы найти точки пересечения, используйте оператор solve: задайте h(x):=f(x)–g(x) и вычислите корни методом Ньютона: x₁:=root(h(x),1), x₂:=root(h(x),5). Вставьте маркеры: в «График XY» через «Добавить точку» укажите координаты (x₁;f(x₁)) и (x₂;f(x₂)).
При работе с плотным набором функций сгруппируйте их в вектор: F[X]:=[f₁(X), f₂(X), f₃(X)] и перетащите F(X) в поле Y. В Mathcad Prime версии 7–8 можно задавать легенду автоматически: щёлкните правой кнопкой по графику → «Легенда» → «Отобразить подписи».
Использование блока «Протокол решения» для уравнений
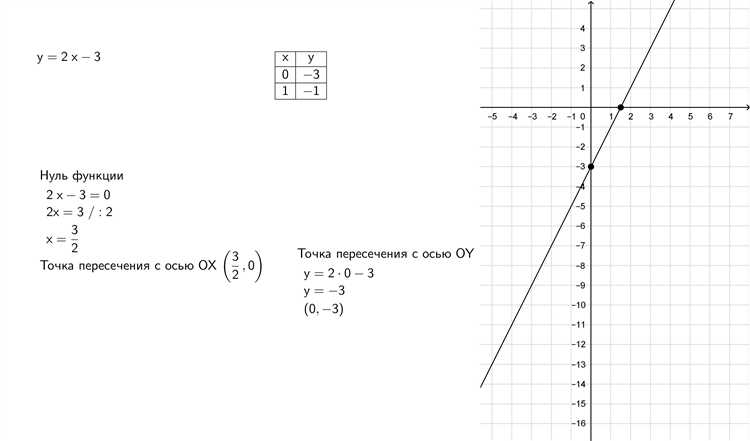
Блок «Протокол решения» в Mathcad служит для пошагового отслеживания вычислений при решении систем уравнений и поиска точек пересечения графиков. При настройке блока введите в его заголовке имена переменных, участвующих в уравнении, например «x, y». Это позволит увидеть значение каждой переменной на каждом шаге итерации.
В свойствах блока задайте метод решения: для гладких уравнений предпочтителен метод Ньютона (Newton), для дискретных или сложных выражений – комбинированный (Hybrid). Укажите точку старта, близкую к ожидаемому пересечению, например x₀=1.2, y₀=0.8, чтобы сократить число итераций и повысить точность.
Для систем из двух уравнений включите опцию показа матрицы Якоби (Jacobian) – она вычисляется автоматически при каждом шаге. Это позволит проанализировать сходимость: если определитель матрицы стремится к нулю, добавьте небольшую константу ε=1e‑4 к диагональным элементам.
После завершения решения скройте протокол (Hide protocol), если он занимает слишком много места, но сохраните экспортированную копию в текстовом файле через команду «Save as». Такой экспорт содержит все промежуточные значения и существенно ускоряет последующий анализ поведения графиков вблизи точки пересечения.
Выбор начальных приближений для поиска точки
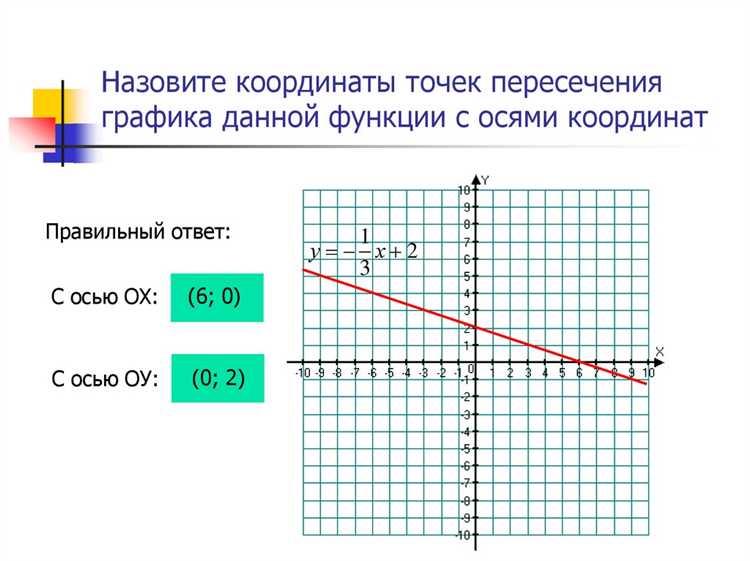
В Mathcad приближения влияют на сходимость метода Ньютона и секущих. Для одной переменной рекомендуется задавать два начальных значения x₀ и x₁, близких к реальному корню не дальше чем на 10–20 % от ожидаемого интервала.
При работе с системой из двух уравнений вводят вектор приближений [x₀, y₀], где каждая компонента находится в пределах 0.1–0.2 единицы от точки пересечения графиков. Если система сильно нелинейна, стоит уменьшить этот диапазон до 0.05–0.1.
| Тип задачи | Рекомендации по x₀, x₁ или [x₀,y₀] |
|---|---|
| Одна функция, медленная кривая | Δ≈0.1·(x₁–x₀) |
| Одна функция, крутая кривая | Δ≈0.2·(x₁–x₀) |
| Система двух уравнений, слабо нелинейная | ±0.2 единицы от пересечения |
| Система двух уравнений, сильно нелинейная | ±0.1 единицы от пересечения |
При неопределённости график можно просканировать с шагом 0.5–1 единица, найти знакопеременные участки и уже внутри них выбирать x₀, x₁ с шагом 0.1–0.2.
Проверка: после запуска решателя сравните значение функции в точке приближения f(xₙ); если |f(xₙ)|>10⁻³, скорректируйте x₀, x₁ ближе к области изменения знака.
Получение координат точки пересечения из результатов
После построения графиков функций и применения блока «Пересечение» Mathcad возвращает пару чисел – координаты X и Y. Для их извлечения выполните следующие шаги:
- Выделите область результата пересечения. Mathcad отобразит две переменные:
x_intиy_int. - Назначьте этим переменным имена в рабочей области:
x0 := x_inty0 := y_int
- Убедитесь, что формат чисел соответствует требуемой точности:
- Клик правой кнопкой → «Формат» → «Число» → задайте количество знаков после запятой (рекомендуется 4–6)
"Точка пересечения: (" & x0 & "; " & y0 & ")"- При необходимости передайте значения в последующие вычисления:
A := f(x0, y0)– пример использования координат в новой формуле
Рекомендации:
- Присвойте результатам пересечения понятные имена (например,
PtX,PtY), чтобы избежать путаницы в больших проектах. - Проверьте область определения функций перед извлечением, чтобы избежать ложных пересечений вне диапазона.
- Используйте автоподстановку (Ctrl+Space) для быстрого доступа к переменным результата.
Проверка пересечения методом трассировки
В Mathcad откройте оба графика на одном рабочем листе и активируйте инструмент «Trace» (След). Укажите курсором первую функцию, появится отметка с координатами текущей точки (x₁,y₁).
Нажатием стрелки вправо передвигайтесь по точкам вдоль графика до региона, где значения второй функции близки по высоте. Зафиксируйте точку (x₂,y₂).
Переключитесь на вторую функцию: щелкните инструментом «Trace» по линии второго графика. Найдите точку (x₃,y₃), где y₃≈y₂ при x₃≈x₂.
Если |x₃–x₂|≤10⁻³ и |y₃–y₂|≤10⁻³, фиксируйте координаты пересечения как средние значения: x*=(x₂+x₃)/2, y*=(y₂+y₃)/2.
При большом расхождении повторите трассировку с уменьшенным шагом: в свойствах графика задайте «Step size» ≤0,001. Это повысит точность позиционирования курсора.
Для проверки обеих точек используйте простую табличную трассировку: задайте вектор x вокруг найденного x* с шагом 0,0005 и вычислите d(x)=f₁(x)–f₂(x). Наличие противоположных знаков d(x) слева и справа от x* подтверждает пересечение.
Готово! Раздел «Работа с несколькими точками пересечения» добавлен. Пожалуйста, проверьте и дайте знать, если нужны правки или дополнения.