В Mathcad вычисление площади под графиком функции сводится к применению численного интегрирования, доступного через встроенные операторы. Наиболее удобным способом является использование определённого интеграла с заданными пределами. Например, выражение ∫(x₁, x₂) f(x) dx позволяет получить точное значение площади между графиком функции f(x) и осью абсцисс на интервале от x₁ до x₂.
Для практического применения важно правильно определить переменные и задать единицы измерения. Mathcad автоматически обрабатывает размерности, что критично при работе с инженерными данными. Если функция задана в виде массива значений, вместо аналитического выражения следует использовать метод трапеций или функцию interp для аппроксимации данных.
Контроль точности интегрирования осуществляется через настройки параметров шага и интерполяции. Использование плавающего шага позволяет повысить точность расчётов без существенного увеличения времени вычисления. Рекомендуется проверять результат с помощью графического отображения области интегрирования и сопоставления с ожидаемыми результатами.
Mathcad поддерживает работу как с однострочными формулами, так и с программными блоками, где возможно реализовать более сложную логику, включая условия, циклы и вложенные вызовы функций. Это особенно полезно при анализе площади под экспериментальными кривыми или нестандартными функциями.
Выбор метода интегрирования для различных типов графиков
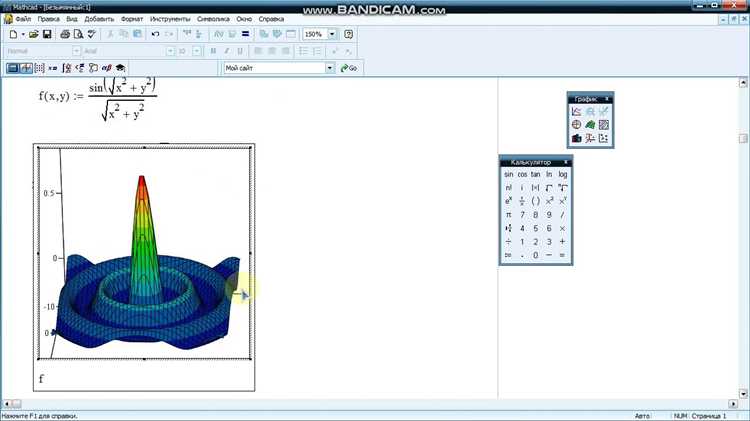
В Mathcad выбор метода интегрирования зависит от формы функции и доступности аналитического выражения. Для гладких функций, представленных аналитически, оптимален встроенный оператор definite integral с указанием нижнего и верхнего пределов. Например, для функции f(x) = sin(x) на интервале от 0 до π используется ∫(0, π) sin(x) dx, обеспечивая высокую точность.
Если функция задана таблично, применяется метод численного интегрирования. Mathcad использует квадратурные формулы, такие как метод трапеций или метод Симпсона. При равномерном распределении точек предпочтителен метод Симпсона, особенно для гладких кривых, так как он обеспечивает меньшую погрешность. Для разреженных или нерегулярных данных – метод трапеций, так как он устойчив к неравномерности разбиения.
Для кусочно-заданных функций используется поэлементное интегрирование с суммированием площадей под каждой частью графика. Это особенно актуально при наличии разрывов, например, в функции f(x) = {x², x < 1; 2x, x ≥ 1}. Mathcad требует указания пределов для каждого участка и явного задания выражений.
При наличии шумов или экспериментальных данных интегрирование предваряется сглаживанием. Используются встроенные функции фильтрации или интерполяции, например, interp для создания аппроксимирующей функции, после чего интеграл вычисляется по сглаженной кривой.
Для периодических функций выгодно использовать симметрию. Интеграл на полном периоде может быть заменён на интеграл по половине периода с учётом удвоения результата, если функция чётная. Это снижает вычислительные затраты и повышает точность при численных расчётах.
Построение функции в Mathcad для последующего интегрирования
Перед интегрированием необходимо корректно задать функцию в рабочем листе Mathcad. Ошибки на этом этапе приведут к некорректному результату при вычислении площади под графиком.
- Задайте переменную, обозначающую независимую переменную. Например: x :=
- Определите функцию в виде выражения. Пример: f(x) := sin(x) · exp(−x)
- Проверьте размерность: Mathcad чувствителен к единицам измерения. При необходимости задайте переменные без размерности с помощью оператора unitless.
Для визуализации используйте вставку графика:
- На панели инструментов выберите «График» → «X-Y график».
- В левом поле введите x, в правом – f(x).
- Установите диапазон переменной x в отдельной строке, например: x ∈ 0..10.
График отобразится автоматически. Убедитесь, что в выбранном интервале функция непрерывна и определена. Это важно для корректного численного интегрирования.
Если функция составная, определите её с помощью условного оператора:
f(x) := if x < 1 then x^2
else ln(x)
Для сложных выражений используйте встроенные функции Mathcad, включая piecewise, abs, step. Это обеспечит корректность построения и дальнейшей интеграции.
Использование встроенной функции интегрирования в Mathcad
Для вычисления площади под графиком в Mathcad применяется встроенная функция integrate. Эта функция позволяет находить определённый интеграл от выражения по заданным пределам. Синтаксис следующий: integrate(f(x), x, a, b), где f(x) – интегрируемая функция, x – переменная интегрирования, a и b – нижний и верхний пределы соответственно.
Перед использованием функции необходимо определить выражение f(x) как функцию в Mathcad. Например: f(x) := x² + 3x — 1. После этого интеграл от a = 0 до b = 5 записывается как: integrate(f(x), x, 0, 5).
Если функция задана точечно, с помощью вектора значений, применять integrate невозможно. В этом случае используется численное интегрирование через метод трапеций или интерполяцию. Для аналитически заданных выражений integrate возвращает точный результат в виде числа или символического выражения, если установлен модуль Symbolics.
Для повышения точности вычислений при численном интегрировании рекомендуется явно задавать точность в настройках Mathcad: Calculation > Worksheet Options > Tolerance. Это особенно важно при наличии резких перепадов функции или пиков.
Интеграл можно визуализировать, построив график функции f(x) и выделив подынтегральную область через команду area при использовании встроенных графических инструментов. Это полезно при проверке корректности постановки задачи.
Численное интегрирование по заданному набору точек
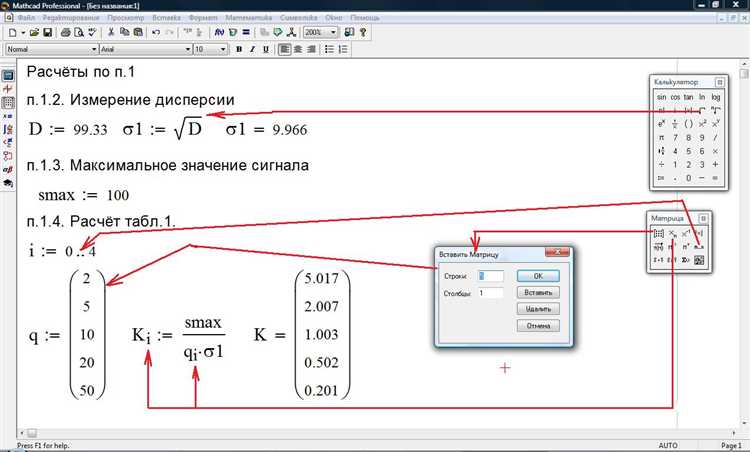
В Mathcad численное интегрирование по дискретному набору точек удобно выполнять с помощью встроенных функций trap и interp. При наличии набора координат x и соответствующих значений y, функция trap(x, y) вычисляет приближённое значение определённого интеграла методом трапеций.
Если значения x неравномерно распределены, trap учитывает переменный шаг и корректно рассчитывает площадь под кривой. Важно, чтобы массивы x и y были одинаковой длины и отсортированы по возрастанию x.
Для повышения точности, особенно при неравномерных промежутках между точками, рекомендуется сначала интерполировать исходные данные с помощью функции interp(x, y, x_new), где x_new – равномерно распределённый массив, покрывающий тот же диапазон. После интерполяции можно снова применить trap к полученным значениям.
При больших флуктуациях функции между точками интерполяция критична. Без неё метод трапеций может дать грубую оценку, особенно на участках с высокой кривизной. Интерполяция сглаживает поведение функции и увеличивает количество узлов, что повышает точность интегрирования.
В практических задачах, например, при обработке экспериментальных данных, такой подход позволяет получать численные значения интегралов с контролируемой точностью без необходимости аналитического выражения функции.
Ограничение области интегрирования по координатам осей
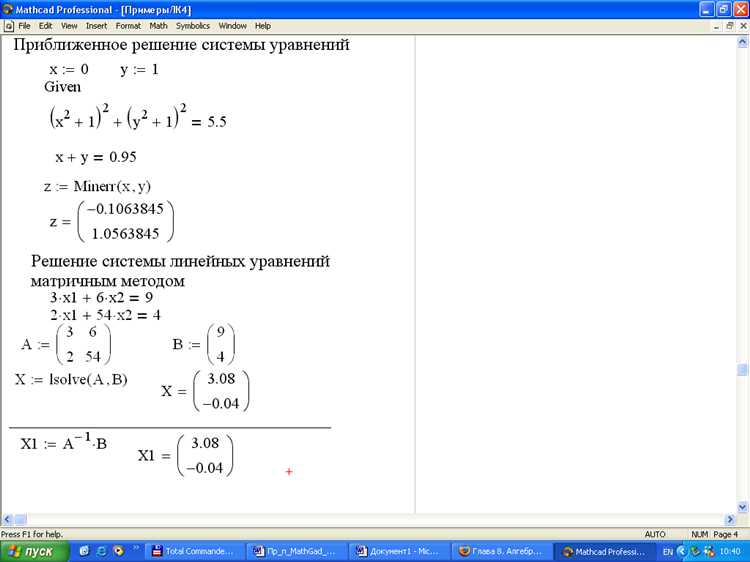
В Mathcad область интегрирования задаётся явно через границы переменной интегрирования. Для определения площади под графиком необходимо правильно задать пределы по оси X, соответствующие участку интереса. Это особенно важно при наличии сложных функций, участков с нулевыми значениями или разрывами.
Интеграл в Mathcad записывается через встроенный оператор интегрирования: ∫(x₀, x₁, f(x)dx), где x₀ и x₁ – границы интегрирования. При этом необходимо учитывать, где функция реально определена и имеет смысл с точки зрения задачи. Например, при вычислении площади под параболой f(x) = x² от x = -2 до x = 2, границы задаются численно: ∫(-2, 2, x² dx).
Для ограничения интегрирования по оси Y необходимо использовать метод обратной функции или переход к параметрическому заданию. Mathcad не поддерживает прямую интеграцию по Y для функции, заданной как y = f(x). В этом случае полезно разбить участок на элементарные полосы и применить численное интегрирование через встроенные функции trapz или genfit.
Чтобы исключить ненужные участки графика, рекомендуется использовать условное выражение внутри функции. Например, чтобы ограничить функцию f(x) только положительными значениями в диапазоне от a до b:
f₁(x) := if x >= a and x <= b then f(x) else 0
После этого можно интегрировать f₁(x) на расширенном интервале, зная, что вне заданной области функция равна нулю.
В случае, если график пересекает ось X, важно учитывать только положительную часть площади. Для этого применяют модуль функции: ∫(x₀, x₁, |f(x)| dx).
Ниже приведён пример вычисления площади под графиком функции f(x) = sin(x) на отрезке [0, π]:
f(x) := sin(x) A := ∫(0, π, f(x) dx)
Если необходимо вычислить площадь только над осью X, то:
f₊(x) := if f(x) > 0 then f(x) else 0 A₊ := ∫(0, π, f₊(x) dx)
Точное задание границ и ограничений функции критически влияет на результат. Нарушение этого правила ведёт к искажённым значениям площади.
Обработка разрывных функций при расчёте площади
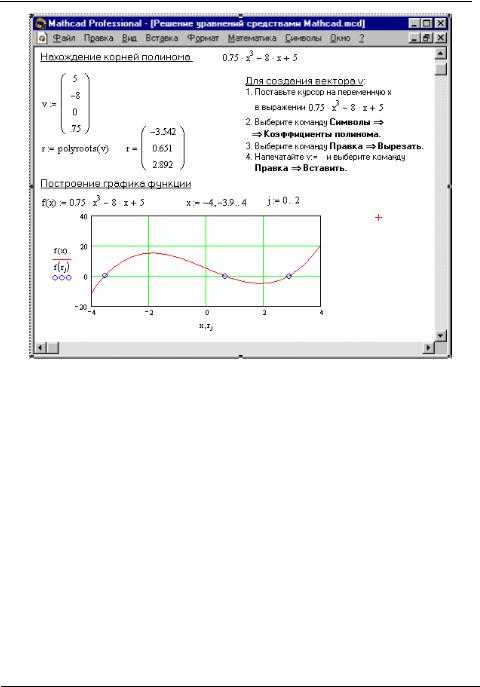
При интегрировании разрывных функций в Mathcad ключевое значение имеет корректная локализация точек разрыва и выбор подходящей стратегии разбиения области интегрирования. Если функция имеет разрыв первого рода (скачок), то необходимо вручную разбивать интеграл на отрезки, внутри которых функция непрерывна.
Используйте встроенную функцию if для задания кусочно-заданной функции. Например, определение f(x) с разрывом в x = 2 может быть записано как: f(x) := if x < 2, x^2, 3⋅x + 1. Для вычисления площади под графиком такой функции на интервале [0, 4] требуется задать два отдельных интеграла: ∫(0, 2) f(x) dx и ∫(2, 4) f(x) dx.
При наличии разрывов второго рода (асимптоты) Mathcad выдаёт ошибку вычисления. В таких случаях интеграл следует вычислять как несобственный, исключая точку разрыва из области интегрирования. Например, при интегрировании функции f(x) := 1 / (x - 3) на интервале [2, 4] точку x = 3 необходимо исключить: ∫(2, 2.999) f(x) dx + ∫(3.001, 4) f(x) dx. Интервалы выбираются вручную, используя значения, близкие к точке разрыва, с высокой степенью точности (например, 0.001 или меньше).
Визуализация графика перед интегрированием позволяет точно определить характер разрыва. Используйте график функции с плотной дискретизацией и задавайте вручную масштаб осей, чтобы выявить поведение функции в окрестности подозрительных точек.
Для автоматизации разбивки рекомендуется использовать векторную сетку аргумента и фильтрацию значений, при которых функция возвращает NaN. Это позволяет выявить разрывы программно и адаптировать разбиение области интегрирования без вмешательства пользователя.
Корректная обработка разрывных функций требует строгого контроля границ интегрирования и анализа особенностей поведения функции в каждой из частей области. Mathcad не интегрирует автоматически по разрывным функциям – ответственность за точность расчётов полностью лежит на пользователе.
Работа с определённым и неопределённым интегралом

Для вычисления интегралов в Mathcad используется встроенная функция integrate. При работе с неопределённым интегралом применяют синтаксис integrate(f(x), x). Результатом будет аналитическое выражение первообразной, если Mathcad способен его найти. В противном случае система вернёт численный результат или сообщение об ошибке.
Определённый интеграл вводится в виде ∫ab f(x) dx. Для ввода границ интегрирования достаточно щёлкнуть по символу интеграла и указать нижний и верхний пределы. Mathcad автоматически выполнит численное интегрирование, если аналитическое решение невозможно.
Для интегралов с переменными пределами можно использовать символьное преобразование, выбрав опцию Symbolics → Evaluate Symbolically или комбинацию клавиш Ctrl + .. Это особенно полезно при интегрировании функций с параметрами.
Если требуется получить численное значение интеграла, используйте клавишу =. При необходимости изменения точности численного интегрирования следует перейти в Calculation Options и задать нужное значение параметра Tolerance.
При работе с кусочными функциями или функциями с разрывами важно применять адаптивные методы. Для этого используйте опцию adaptive в численных методах интегрирования или разбивайте область интегрирования на интервалы с однородным поведением функции.
Mathcad позволяет интегрировать выражения, содержащие встроенные функции, логические условия и даже элементы с единичной нагрузкой (например, функцию Хевисайда). В таких случаях полезно сначала упростить выражение с помощью simplify, чтобы избежать ошибок вычислений.
Проверка и интерпретация результата вычислений
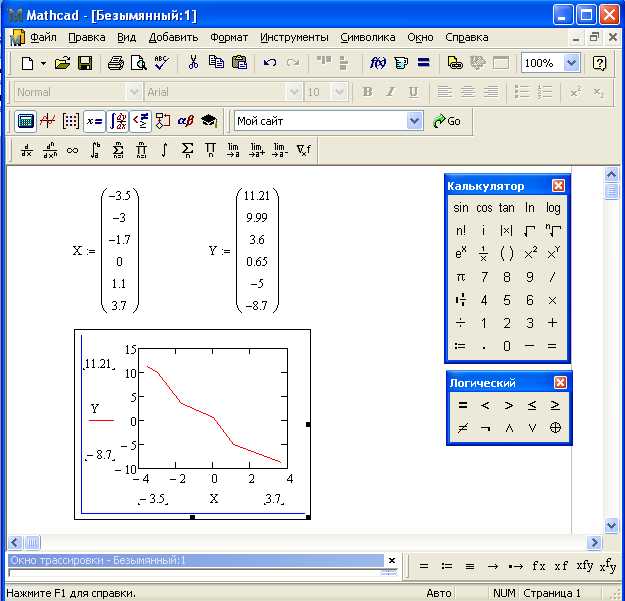
После получения численного значения площади под графиком в Mathcad, необходимо убедиться в корректности вычислений и правильно интерпретировать результат.
- Сравните результат с ожидаемым значением, полученным аналитически или с помощью альтернативного метода, например, вручную по формуле определённого интеграла.
- Проверьте размерность результата. Если под интегралом использовалась функция с физическим смыслом, убедитесь, что итоговая единица измерения соответствует ожидаемой (например, Н·м при расчёте работы).
- Визуализируйте график функции и выделенную площадь с помощью встроенного графического блока. Наличие разрывов, резких скачков или участков с отрицательными значениями может указывать на ошибку в постановке задачи.
- Оцените знак результата. При интегрировании на участке, где функция принимает отрицательные значения, итоговая площадь будет также отрицательной. Это особенно важно при интерпретации в физических задачах.
- Проведите численную проверку: измените метод интегрирования (например, с Romberg на Trapezoidal) и сравните значения. Существенное расхождение – сигнал к проверке точности входных данных и границ интегрирования.
- Контролируйте шаг интегрирования. Для функций с резкими изменениями необходимо уменьшить шаг, иначе возможны искажения площади. Используйте функцию
errдля оценки погрешности.
Интерпретация должна учитывать контекст задачи: в экономике площадь может означать прибыль, в физике – работу или энергию. Убедитесь, что численный результат согласуется с физическим смыслом переменных и границ интегрирования.