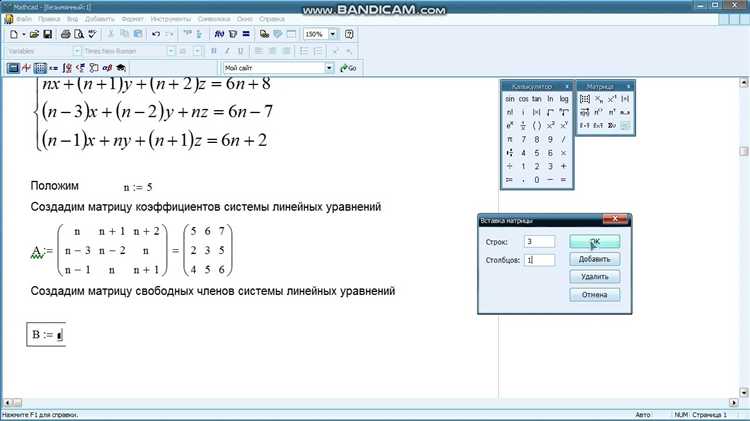
Mathcad позволяет решать системы линейных уравнений как численно, так и аналитически, используя встроенные операторы матричных преобразований. Основной инструмент – функция lsolve(A, b), где A – матрица коэффициентов, а b – вектор свободных членов. Эта функция возвращает вектор решений, при условии, что матрица A невырожденная.
Для удобства рекомендуется вводить матрицу A через двоеточие или вручную, с указанием размеров. Mathcad автоматически проверяет соответствие размеров матрицы и вектора, что исключает логические ошибки на этапе ввода данных. При работе с символьными выражениями используется оператор → и функция solve, что удобно при необходимости получить общее аналитическое решение.
Mathcad поддерживает визуализацию систем уравнений, включая пошаговую проверку решений и промежуточных вычислений. Это особенно полезно при обучении или разборе ошибок в расчетах. При работе с переопределёнными или несовместными системами рекомендуется анализировать определитель матрицы A с помощью функции det(A) и использовать метод наименьших квадратов через функцию lsolve в случае вырожденности системы.
Построение матрицы коэффициентов и столбца свободных членов
В Mathcad система линейных уравнений представляется в виде AX = B, где A – матрица коэффициентов, X – вектор переменных, B – столбец свободных членов. Для корректного решения важно правильно задать матрицу A и вектор B.
Чтобы ввести матрицу коэффициентов A, необходимо использовать клавишу [Ctrl] + M. Появляется шаблон, в который вводятся числовые значения без символов переменных. Размер матрицы должен точно соответствовать количеству уравнений и переменных. Например, для трёх уравнений с тремя переменными вводится матрица 3×3.
Каждая строка матрицы соответствует отдельному уравнению, а каждый столбец – коэффициенту при конкретной переменной. Например, уравнение 2x + 3y — z = 5 преобразуется в строку 2, 3, -1.
Столбец свободных членов B вводится как вектор-столбец с тем же числом строк, что и матрица A. Для этого используется обычное присваивание переменной, например: B := [5, 7, -2]^T, где ^T означает транспонирование вектора-строки в вектор-столбец.
Все элементы матриц и векторов должны быть заданы в числовом виде без переменных. Использование единиц измерения не допускается, если требуется численное решение. Проверка размерности выполняется автоматически – несогласованность размеров приведёт к ошибке вычислений.
Для повторного использования удобно задать матрицы A и B в начале рабочего листа и ссылаться на них в дальнейшем. Это упрощает изменение исходных данных и минимизирует вероятность ошибок при корректировке системы.
Использование оператора решета (solve block) для систем уравнений
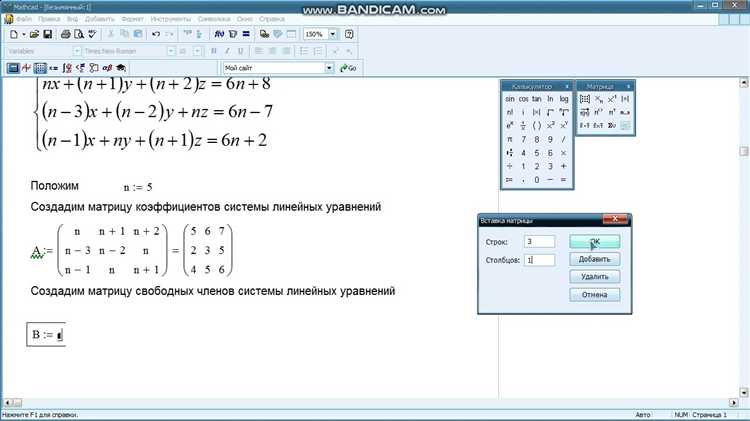
Оператор решета (solve block) в Mathcad применяется для точного решения систем линейных уравнений, в которых количество уравнений равно количеству переменных. Он обеспечивает пошаговую формализацию процесса решения с возможностью задания дополнительных ограничений или начальных приближений.
- Оператор начинается с ключевого слова Given, за которым следует список уравнений.
- Каждое уравнение в блоке должно быть задано с использованием логического знака равенства =, а не вычислительного знака :=.
- После уравнений необходимо вызвать функцию find(var1, var2, …), где var1, var2 – искомые переменные.
Пример для трёх уравнений с тремя переменными:
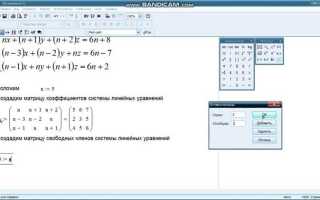
Given x + y + z = 6 2x - y + 3z = 14 -x + 4y - z = -2 find(x, y, z)
Особенности использования:
- Оператор чувствителен к размерности выражений – количество уравнений должно соответствовать числу переменных.
- Недопустимо использовать присваивание внутри блока – только логическое сравнение.
- Если решение не существует или система вырождена, Mathcad вернёт ошибку либо комплексные значения – это требует дополнительного анализа условий.
Для параметрически заданных систем можно использовать solve block совместно с элементами интерфейса, такими как ползунки или управляющие переменные, что позволяет визуализировать влияние параметров на решение.
В отличие от матричного способа, solve block позволяет легко работать с символическими переменными и получать аналитическое представление решения через symbolics → solve.
Для улучшения читаемости и отладки рекомендуется отделять блок решета от остального расчёта, а результаты сохранять в отдельные переменные для последующего использования или визуализации.
Применение встроенной функции lsolve для получения численного решения

Функция lsolve в Mathcad используется для численного решения системы линейных уравнений вида A·x = b, где A – квадратная матрица коэффициентов, x – вектор неизвестных, b – вектор свободных членов. Для корректной работы размерность A должна совпадать с размерностью b.
Входные данные вводятся в виде матрицы A и вектора b. Затем применяется вызов: x := lsolve(A, b). Результатом является вектор x, содержащий численные значения переменных. Все элементы матрицы и вектора должны быть определены численно до вызова lsolve.
Функция автоматически использует LU-разложение для решения, что позволяет эффективно обрабатывать системы с хорошо обусловленными матрицами. При наличии вырожденной или плохо обусловленной матрицы результат может содержать большие погрешности. В таких случаях рекомендуется предварительно проанализировать определитель матрицы A и число обусловленности с помощью функций det(A) и cond(A).
Для повышения точности рекомендуется избегать ручного ввода приближённых значений и использовать как можно больше значащих цифр. Кроме того, при работе с параметризованными уравнениями удобно использовать lsolve в комбинации с оператором программирования for для получения серии решений при разных параметрах.
Функция lsolve не требует символьных преобразований и работает исключительно с числовыми данными. Это делает её оптимальной для задач инженерного расчета, где известны все коэффициенты и требуется быстрое получение результата.
Обработка ошибок несовместных и вырожденных систем
В Mathcad при решении системы линейных уравнений с использованием встроенной функции lsolve(A, b) необходимо контролировать структуру матрицы коэффициентов A. Если система несовместна, Mathcad возвращает ошибку типа «This value must be a real number», что указывает на отсутствие решения при заданном векторе b.
Для диагностики несовместности следует использовать ранговый анализ: вычислить ранг матрицы A и расширенной матрицы [A|b] с помощью функции rank(). Если rank(A) ≠ rank([A|b]), система несовместна. В этом случае необходимо пересмотреть исходные данные или использовать метод наименьших квадратов lstsq(A, b) для получения приближённого решения.
Вырожденные системы возникают при линейно зависимых строках матрицы A. Если det(A) = 0 или rank(A) < cols(A), система имеет бесконечное число решений или не имеет их вовсе. Перед использованием lsolve следует проверить невырожденность: if det(A) ≠ 0 then x := lsolve(A, b). В противном случае – применять lstsq или анализировать пространство решений вручную, используя функции nullspace(A) и rref(A).
Для избежания ошибок в расчетах рекомендуется всегда проверять размерность матрицы, ее ранг, а также наличие линейной зависимости между строками и столбцами. Это обеспечивает контроль корректности постановки задачи и позволяет обрабатывать особые случаи без сбоев в вычислениях.
Визуализация решений с помощью графических элементов Mathcad

Для анализа системы линейных уравнений в Mathcad рекомендуется использовать графические элементы, такие как 2D и 3D-графики. Это особенно полезно при визуализации решений систем с двумя или тремя переменными.
При решении системы вида:
A := [ [2, -1], [1, 3] ] b := [4, 7 x := lsolve(A, b)
можно построить графики линий, соответствующих каждому уравнению. Для этого следует выразить каждое уравнение явно и отобразить на координатной плоскости:
y1(x) := (2x - 4) y2(x) := (7 - x) / 3
Далее вставляется 2D-график через меню «Insert → Graph → X-Y Plot». В окно графика перетаскиваются функции y1(x) и y2(x), диапазон переменной x задается вручную, например от -10 до 10. Точка пересечения графиков указывает на решение системы.
Для трёхмерных систем, например:
A := [ [1, 2, -1], [2, -1, 3], [3, 1, 2] ] b := [2, 5, 7 x := lsolve(A, b)
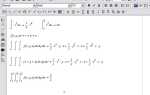
можно визуализировать плоскости, соответствующие каждому уравнению. Каждое уравнение преобразуется к виду z = f(x, y). Например, первое уравнение z = x + 2y — 2. Через «Insert → Graph → Surface Plot» создаются графики плоскостей. В область построения добавляется по одному выражению для каждой плоскости.
При наложении нескольких поверхностей на один график необходимо варьировать цвет и прозрачность. Это настраивается вручную в свойствах каждой поверхности, чтобы увидеть точку пересечения плоскостей – решение системы.
Рекомендуется использовать сетку (grid lines), задавать точные диапазоны переменных и подписывать оси через «Trace → Format». Также полезно включать маркеры (markers) в точке решения системы с помощью координат, полученных из lsolve.
Визуализация помогает проверить корректность аналитического решения и оценить чувствительность системы к изменению коэффициентов.
Сравнение точных и численных методов решения систем

Точные методы, такие как метод Крамера или приведение к ступенчатому виду, гарантируют получение решения с машинной точностью при наличии невырожденной матрицы коэффициентов. В Mathcad эти методы реализованы через встроенные функции для вычисления определителей и обратных матриц. Однако при размерности системы выше 10–15 переменных точные методы становятся вычислительно затратными и подвержены ошибкам округления, особенно при плохо обусловленных системах.
Численные методы, в частности метод LU-разложения или итерационные алгоритмы (Гаусса-Зейделя, Якоби), обладают устойчивостью к ошибкам округления и масштабируются лучше при больших размерах систем. Mathcad позволяет эффективно применять эти методы с помощью встроенных функций и векторных операций. Итерационные методы предпочтительны при разреженных матрицах и когда точное решение не требуется с высокой точностью, достаточно с заданной погрешностью.
Рекомендации: для систем размером до 10 переменных оптимально использовать точные методы для минимизации ошибок накопления. При размере свыше 20 переменных и особенно при наличии условно малых определителей эффективнее применять численные алгоритмы с контролем сходимости. В задачах с разреженными или плохо обусловленными матрицами стоит отдавать предпочтение итерационным численным методам с регуляризацией.
В Mathcad важна настройка параметров точности и ограничений итераций при численных методах. Неправильный выбор может привести к отсутствию сходимости или слишком длительным вычислениям. Поэтому комбинированный подход – предварительное упрощение системы и выбор метода с учетом структуры матрицы – обеспечивает баланс между скоростью и точностью решения.
Вопрос-ответ:
Как в Mathcad задать систему линейных уравнений для решения?
Для задания системы линейных уравнений в Mathcad обычно используют матричный формат. Сначала нужно определить коэффициенты уравнений в виде матрицы, а затем — вектор свободных членов. После этого можно применить встроенные функции для вычисления решения, например, оператор обратной матрицы или функцию решения систем. В Mathcad удобно работать с матрицами благодаря наглядному интерфейсу, где каждая строка соответствует уравнению, а каждый столбец — переменной.
Какие методы решения систем линейных уравнений доступны в Mathcad и как выбрать подходящий?
Mathcad предлагает несколько способов решения систем линейных уравнений, включая метод обратной матрицы, метод Крамера и численные методы, такие как LU-разложение. Для небольших систем с точно заданными коэффициентами достаточно использовать метод обратной матрицы, но при больших или плохо обусловленных системах лучше применять численные методы. Выбор зависит от размера системы и требований к точности решения.
Как проверить корректность решения системы уравнений в Mathcad?
После получения решения в Mathcad можно подставить найденные значения переменных обратно в исходные уравнения, чтобы убедиться, что левая часть уравнений равна правой с допустимой погрешностью. Также можно вычислить невязку — разницу между результатом подстановки и исходным значением. Невязка близкая к нулю говорит о правильности решения. Mathcad позволяет автоматически выполнять такие проверки с помощью встроенных функций.
Можно ли решать системы уравнений с параметрами в Mathcad, и как это сделать?
Да, Mathcad позволяет работать с системами, в которых некоторые коэффициенты представлены в виде параметров. Для этого параметры задаются как переменные с определёнными значениями или диапазонами, а затем система решается либо для конкретных значений, либо с помощью численного анализа при изменении параметров. Такой подход удобен для исследования зависимости решений от входных данных.