Как найти производную в maple

Maple предоставляет встроенную функцию diff для дифференцирования выражений. Чтобы вычислить производную, достаточно вызвать diff с нужной функцией и переменной, например: diff(f(x), x). Этот вызов мгновенно вернёт аналитическое выражение производной.

Для ускорения работы с производными используйте упрощение результата с помощью функции simplify, особенно при сложных выражениях. Это помогает получить компактную форму и облегчить последующий анализ.

При работе с многопеременными функциями Maple позволяет вычислять частные производные, используя несколько переменных в вызове diff. Для быстрого получения второй и высших производных используйте указание степени, например: diff(f(x), x$2) вычисляет вторую производную по x.

Подготовка выражения к дифференцированию в Maple

Перед вычислением производной в Maple важно привести выражение к корректному синтаксису системы. Убедитесь, что все функции и операции заданы в формате, распознаваемом Maple: тригонометрические функции пишутся как sin(x), cos(x), логарифмы – ln(x), экспоненты – exp(x). Для степеней используйте символ ^, а не ** или другие альтернативы.

Если выражение содержит константы или параметры, объявите их с помощью команды assume, чтобы Maple учитывал их свойства при дифференцировании (например, положительность или вещественность). Это предотвратит появление лишних условий в результате.

Для сложных выражений рекомендуется предварительно упростить их с помощью команд simplify или expand, чтобы избежать избыточной громоздкости результата. Также можно использовать convert для приведения выражений к нужной форме, например, из тригонометрической в алгебраическую.

Если переменная дифференцирования не указана явно, Maple принимает переменную по умолчанию. Для точности указывайте её явно: diff(выражение, переменная). Это особенно важно при наличии нескольких переменных.

Перед дифференцированием проверьте корректность ввода: ошибочные скобки или неправильное использование операторов приведут к неверному результату или ошибке выполнения. Используйте команду print или eval для проверки промежуточного результата.

Команда diff: синтаксис и базовое использование

В Maple команда diff служит для вычисления производных функций. Основной синтаксис выглядит так: diff(f, x), где f – выражение или функция, а x – переменная, по которой берётся производная.

Для производной высшего порядка используется форма diff(f, x$n), где n – порядок производной. Например, diff(sin(x), x$3) вычисляет третью производную синуса по x.

Если требуется взять производную по нескольким переменным, они перечисляются подряд: diff(f, x, y) вычисляет смешанную частную производную сначала по x, затем по y.

Команда поддерживает дифференцирование выражений, содержащих параметры и функции. В таких случаях Maple оставит результат в символической форме, если переменная не задана явно.

Важно: при работе с параметрами без указания переменной diff не сможет вычислить производную и вернёт исходное выражение.

Для быстрого вычисления производной достаточно ввести diff(f, x), где f – любая функция, заданная в текущем сеансе. Maple автоматически упрощает результат и возвращает его в наиболее компактной форме.

Поиск производной сложной функции с несколькими переменными

В Maple вычисление частных производных сложных функций нескольких переменных реализуется через встроенную команду diff. Для корректного результата важно четко задать переменные и порядок дифференцирования.

1. Объявление переменных: перед вычислением производной необходимо определить все переменные функции с помощью variables := [x, y, z]; или аналогичной записи.
2. Вычисление частной производной: команда diff(f, x) возвращает частную производную функции f по переменной x.
3. Производные высших порядков: для второго порядка используйте diff(f, x$2), для смешанных частных производных – diff(f, x, y).
4. Работа с композициями функций: если функция сложная и содержит вложенные выражения, Maple автоматически применит правило цепочки, но рекомендуется использовать simplify или expand для упрощения результата.
5. Дифференцирование векторных функций: для векторных или матричных функций используйте дифференцирование поэлементно с циклом или функцией map с diff.

Пример вычисления частной производной сложной функции:

f := (x, y) -> sin(x^2 + y^2)*exp(x*y);
diff(f(x,y), x);

Для частных производных по нескольким переменным в одном выражении:

diff(f(x,y), x, y);

Maple позволяет использовать D-оператор для дифференцирования функций, что удобно для функционального подхода и упрощает вычисления при большом числе переменных.

Автоматическое упрощение результата производной

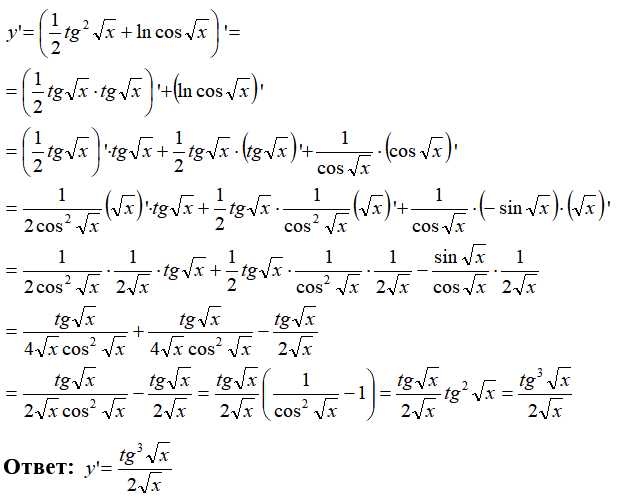
Maple по умолчанию возвращает производную в виде выражения, не всегда оптимально упрощённого. Для автоматического упрощения результата используйте функцию simplify(). После вычисления производной вызов simplify(diff(f(x), x)) преобразует выражение к более компактному виду, устраняя избыточные скобки, объединяя подобные члены и упрощая дроби.

Для более глубокого упрощения применяйте опции внутри simplify(), например, simplify(expr, symbolic) или simplify(expr, trig) для тригонометрических выражений. Если результат содержит сложные алгебраические структуры, можно использовать factor() для разложения на множители и combine() для объединения логарифмов или степеней.

Для автоматизации процесса вычисления и упрощения удобно использовать цепочку вызовов: simplify(diff(f(x), x)) или определить собственную функцию, которая сразу возвращает упрощённый результат. Это особенно важно при работе с многочленами, рациональными выражениями и сложными функциями, где ручное упрощение затратно по времени.

Использование параметра radical внутри simplify() помогает избавиться от избыточных корней, а evalf() позволяет получить числовое приближение, если аналитическая форма не нужна. Таким образом, комбинируя diff и simplify с нужными опциями, вы получаете максимально читаемый и удобный для дальнейших вычислений результат.

Вычисление производной высших порядков в Maple

Для вычисления производных второго и выше порядков в Maple применяется функция diff с указанием степени производной через дополнительный аргумент. Синтаксис: diff(функция, переменная, порядок). Например, diff(f(x), x, 3) вычисляет третью производную функции f(x) по переменной x.

Если функция задана явно, допустимо сразу подставлять выражение, например: diff(sin(x^2), x, 2) – в этом случае Maple автоматически распознает переменную и вычислит вторую производную.

Для многомерных функций порядок производной указывается отдельно для каждой переменной: diff(f(x,y), x$n, y$m) – производная n-го порядка по x и m-го порядка по y. Здесь символ $ отделяет переменную от степени производной.

При вычислении производных высших порядков Maple оптимизирует вычисления, избегая повторного вычисления промежуточных производных. Для повышения производительности рекомендуется сохранять результат промежуточных дифференцирований в переменные.

Особое внимание уделяйте корректному указанию переменной и порядка. Если порядок не задан, Maple вычисляет только первую производную, что может привести к ошибкам при ожидании высших порядков.

В случае необходимости численного вычисления высших производных используйте комбинацию diff с функцией evalf. Например: evalf(diff(f(x), x, 4)) даст численное значение четвертой производной в заданной точке при подстановке.

Экспорт и сохранение результата производной для дальнейшей работы

В Maple результат вычисления производной представлен в виде выражения, которое можно сохранить в переменную для последующей обработки. Например, diff(f(x), x) можно присвоить переменной: df := diff(f(x), x);. Это упрощает повторное использование результата без повторного вычисления.

Для экспорта результата в текстовый файл используйте команду fprintf или функцию TextTools:-Export. Пример с fprintf:

fout := fopen("derivative.txt", WRITE); fprintf(fout, "%a", df); fclose(fout);

При таком подходе сохраняется точное выражение в формате, пригодном для чтения и импорта обратно в Maple.

Для интеграции с другими программами результат можно экспортировать в формат MathML через пакет ExportTools:

ExportTools:-Export("derivative.xml", df, format = MathML);

Это обеспечивает совместимость с системами компьютерной алгебры и текстовыми редакторами, поддерживающими MathML.

Сохранение результата в Maple-файл (.mpl) позволяет структурировать рабочие данные. Команда save сохраняет переменные и выражения:

save df, "derivative.mpl";

При последующей загрузке командой read("derivative.mpl"); переменная df будет восстановлена в рабочем пространстве.

Вопрос-ответ:

Как в Maple найти производную сложной функции с несколькими переменными?

В Maple для нахождения производной функции нескольких переменных нужно использовать команду `diff`. Например, чтобы найти частную производную функции f(x,y) по x, пишут `diff(f(x,y), x)`. Для производной по y — `diff(f(x,y), y)`. Если требуется производная высших порядков, указывают порядок: `diff(f(x,y), x$2)` — вторая производная по x. Maple обрабатывает сложные выражения и позволяет легко получать нужные производные.

Можно ли в Maple получить производную функции, заданной через определённое выражение, без её явного задания?

Да, в Maple есть возможность вычислять производные даже если функция задана не как отдельное имя, а как выражение. Для этого в команду `diff` передают само выражение. Например, если у вас есть выражение `sin(x)^2 + x^3`, чтобы найти его производную, пишут: `diff(sin(x)^2 + x^3, x)`. Maple сразу вычислит производную по переменной x без необходимости создавать функцию.

Как ускорить процесс вычисления производных в Maple при работе с большими формулами?

Для ускорения вычислений стоит использовать встроенные функции Maple, избегая избыточных повторных вычислений. Можно сохранить выражение в переменную, а затем дифференцировать её. Также полезно применять упрощение результата командой `simplify` уже после нахождения производной, чтобы избавиться от лишних частей. Иногда помогает использование пакетов, специализированных на работе с символьными выражениями. Важно контролировать, чтобы переменные были правильно определены, и не было лишних преобразований в процессе.

Какие команды Maple используют для нахождения производных от параметрических функций?

Для параметрических функций, заданных например как x = f(t), y = g(t), производную y по x можно найти через t с помощью цепного правила. В Maple это делают так: сначала вычисляют производные `dx := diff(f(t), t)` и `dy := diff(g(t), t)`, затем берут отношение `dy/dx`. Такой подход позволяет получить производную в явном виде, даже если функция задана параметрически.

Как в Maple найти производную функции с учётом условий, например, при ограничениях на переменную?

Maple позволяет задавать условия для переменных через команды или использовать функцию `assuming`. Например, чтобы найти производную функции f(x) с условием, что x положительно, можно написать: `diff(f(x), x) assuming x > 0`. Это помогает системе правильно учитывать область определения и упрощать производные, соответствующим образом обрабатывая выражения.