Как в mathcad сделать систему уравнений

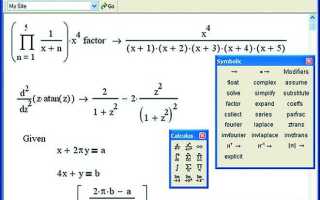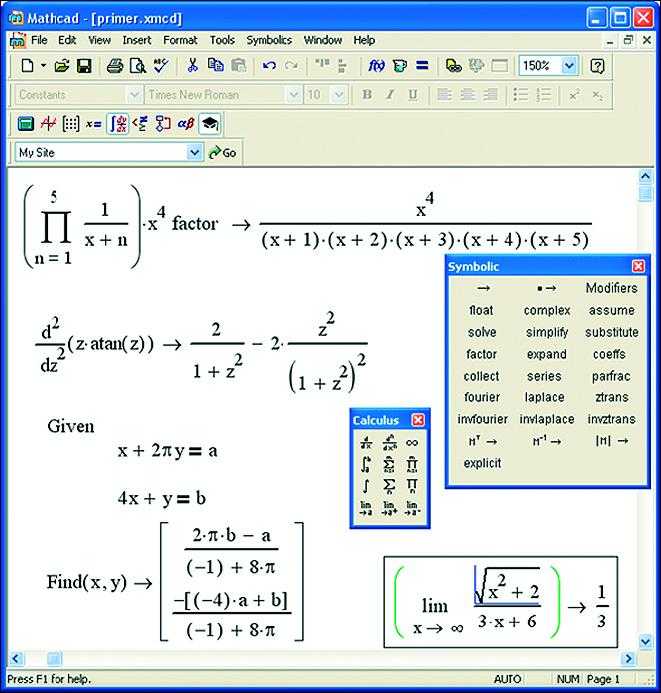
В среде Mathcad решение систем уравнений реализуется с помощью встроенных инструментов, позволяющих работать как с алгебраическими, так и с дифференциальными системами. Для задания системы необходимо использовать операторы векторного ввода и символы локального определения (:=) и вычисления (=).

Сначала объявите переменные: задайте им начальные приближённые значения, если планируется численное решение. Например, переменные x и y можно определить как x := 1, y := 1. Затем создайте вектор уравнений, где каждое уравнение оформляется как выражение, равное нулю, например: eq1 := x + y — 5, eq2 := x — y — 1.

Для объединения уравнений в систему используйте вектор: eqs := [eq1, eq2]. Далее укажите вектор переменных, относительно которых нужно решить систему: vars := [x, y]. Решение производится функцией solve из пакета Given-Find или root, если используется численное решение.

Настройка области определения переменных в Mathcad

Область определения переменной в Mathcad задаётся с помощью оператора двойного двоеточия := или конструкции диапазона. Для задания числового диапазона используйте следующий синтаксис:

x := 0, 0.1 .. 10

Здесь переменной x присваивается диапазон значений от 0 до 10 с шагом 0.1. Такой формат позволяет создавать массив значений, используемый в уравнениях или функциях.

Если переменная зависит от другой, область определения нужно задать после определения зависимости. Например:

y(x) := sin(x)
x := -π, 0.01 .. π

Mathcad автоматически пересчитает y для всего диапазона x.

Для ограничения области вручную используйте логические условия с функцией if или оператор when. Пример с ограничением по условию:

f(x) := if x > 0 then ln(x)

Также можно задать функцию с использованием определения по частям:

g(x) :=

Чтобы избежать ошибок вычислений, всегда проверяйте, что диапазон не вызывает деление на ноль или обращение к значениям вне допустимой области функций. При необходимости применяйте функции exclude или submatrix для фильтрации диапазонов.

Ввод алгебраических уравнений с использованием знака равенства

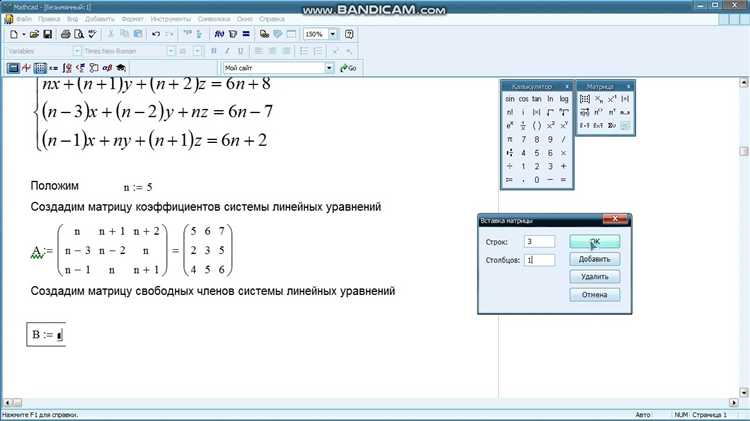
В Mathcad знак равенства = играет две различные роли: вычислительное равенство и символьное (логическое) равенство. Для ввода алгебраических уравнений, предназначенных для решения, необходимо использовать логическое равенство, вводимое с помощью клавиш Ctrl + =. Это важно, поскольку простое = инициирует немедленное вычисление выражения, что делает невозможным задание системы уравнений.

Пример корректного ввода алгебраического уравнения: x^2 + y^2 Ctrl+= 25. После ввода такого выражения Mathcad воспринимает его как часть системы уравнений, а не как команду к вычислению результата.

Не следует путать: x = 5 – это присваивание, Mathcad немедленно подставит значение 5 в переменную x. Для символьной постановки условия следует написать x Ctrl+= 5.

Чтобы избежать ошибок, убедитесь, что при вводе уравнений индикатор := или = не появляется автоматически – в таком случае нужно отменить ввод и повторить с использованием Ctrl + =.

Система уравнений оформляется как последовательность строк с уравнениями, набранными через логическое равенство. Для её решения используется функция solve из встроенного блока solve block – там уравнения должны быть именно в логической форме.

Определение системы уравнений с помощью оператора «solve»

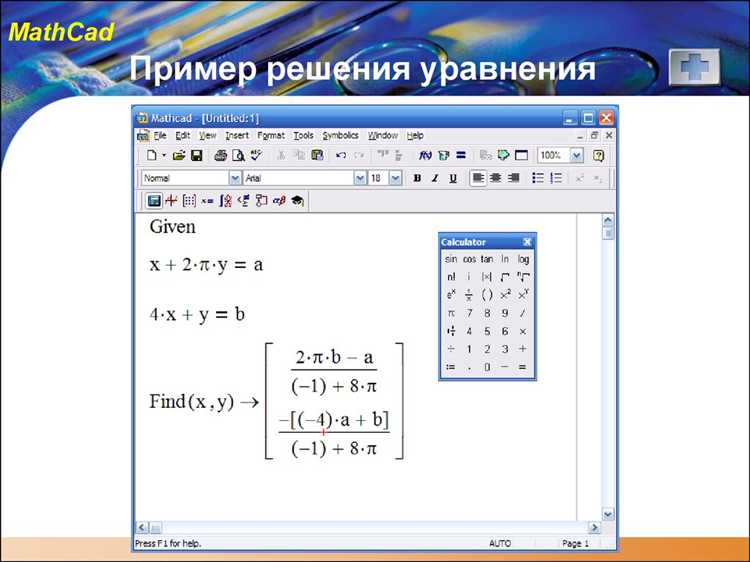
Для задания системы уравнений в Mathcad используйте оператор solve в сочетании с функцией find. Сначала определите все уравнения в виде логических выражений (используйте знак =, а не :=). Уравнения должны быть записаны в виде выражений, возвращающих значение true при верном равенстве.

Пример: необходимо решить систему

x + y = 5

x — y = 1

В Mathcad:

x + y = 5

x — y = 1

solve(x, y) ⟹ find(x, y)

Перед вызовом find убедитесь, что все переменные предварительно не определены численно. Mathcad воспринимает их как неизвестные только в отсутствии числовых значений.

Функция find возвращает список решений в виде вектора. Для обращения к каждому элементу используйте индексацию: find(x, y)[0] – значение x, find(x, y)[1] – значение y.

Если в системе больше уравнений, просто добавляйте их последовательно до вызова solve. Количество уравнений должно соответствовать числу неизвестных.

Нельзя использовать solve для уравнений, содержащих производные, интегралы или условные конструкции. В таких случаях применяйте Odesolve или численные методы оптимизации.

Проверяйте корректность формулировки каждого уравнения. Используйте команду Check (Проверка) в Mathcad для выявления синтаксических и логических ошибок до вычисления решения.

Назначение начальных приближений для численного решения

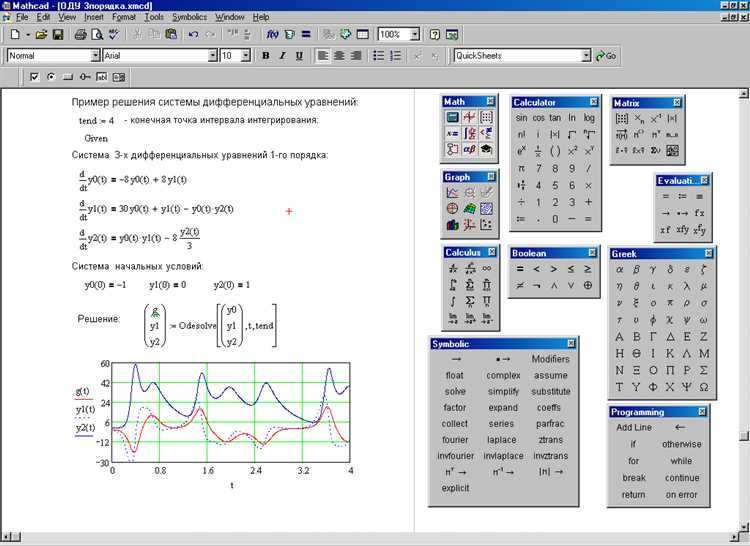
При решении системы нелинейных уравнений в Mathcad с помощью численных методов, таких как функция Find, необходимо задать начальные приближения для переменных. Без них вычисления не будут выполняться.

• Каждой переменной в системе должно быть присвоено числовое значение перед вызовом Find.
• Начальные значения записываются с использованием оператора присваивания ← (левая стрелка), а не знака равенства.
• Рекомендуется выбирать приближения, близкие к ожидаемому решению, особенно при наличии нескольких решений.

Если система чувствительна к начальному выбору, стоит использовать графическое представление функций или анализ границ решений, чтобы определить подходящий диапазон значений.

1. Определи переменные: например, x ← 1, y ← -2.
2. Задай систему уравнений с использованием логического равенства =.
3. Вызови Find(x, y) для численного поиска.

Для многомерных систем ошибочные приближения могут привести к сходимости к неверному решению или к сбою расчёта. Поэтому важно предварительно проверять диапазон значений и при необходимости варьировать начальные точки вручную.

Mathcad не предоставляет автоматического подбора приближений. Ответственность за выбор лежит на пользователе. В случае расхождения стоит попробовать другие стартовые значения или использовать функцию Given-Find в комбинации с условиями ограничений.

Применение функции «find» для получения численного решения

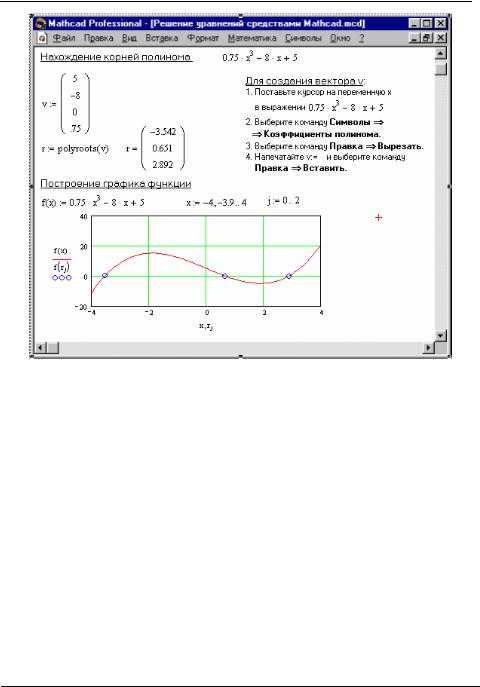
Функция find в Mathcad применяется для численного решения систем нелинейных уравнений. Перед её использованием необходимо определить переменные и задать систему уравнений в виде уравнений-ограничений (constraints) с использованием знака =, а не оператора присваивания :=.

Каждой переменной, которую требуется найти, следует задать начальное приближение с помощью выражений вида x := значение. Это критично для сходимости итерационного метода, применяемого функцией find.

Пример. Пусть требуется решить систему:

x + y = 5
x² + y² = 13

В Mathcad необходимо задать:

x := 1
y := 1
Given
x + y = 5
x^2 + y^2 = 13

После блока Given вызывается функция:

find(x, y)

Результатом будет вектор, содержащий численные значения переменных x и y, удовлетворяющие заданной системе. Функция find работает только в контексте Given. Попытка использовать её без блока приведёт к ошибке.

Для увеличения стабильности решения рекомендуется выбирать стартовые значения, близкие к предполагаемому решению. При наличии нескольких решений – варьировать начальные условия.

Функция find не позволяет контролировать точность напрямую. Для повышения точности следует изменить системные параметры вычислений: Tolerance и Maximum Number of Iterations в меню Math → Calculation Options.

Не поддерживаются символические переменные. Все выражения должны быть полностью численными. Использование условных операторов (if) в уравнениях может нарушить сходимость. Оптимальный подход – выразить все ограничения алгебраически.

Проверка результатов и визуализация решения на графике

После формирования системы уравнений в Mathcad важно проверить корректность вычисленных значений. Для этого сравните численные результаты с аналитическими решениями или подставьте значения переменных обратно в уравнения, используя оператор подстановки :=. Если уравнения не равны нулю, требуется пересмотреть параметры или метод решения.

Для визуализации используйте встроенную функцию построения графиков. Создайте диапазон значений для переменных с помощью оператора диапазона, например, x := 0, 0.1..10. Затем определите выражения, зависящие от этих переменных, и добавьте график через вставку 2D Plot. Это позволит наблюдать поведение функций и выявлять точки пересечения, которые соответствуют решениям системы.

Рекомендуется строить графики для нескольких уравнений одновременно, чтобы наглядно проверить совпадение решений. При наличии комплексных переменных используйте отдельные графики для вещественной и мнимой частей. Убедитесь, что оси графика корректно масштабированы, чтобы избежать искажения данных.

Используйте аннотации и метки на графиках для выделения ключевых точек, таких как корни уравнений или экстремумы. Для динамического анализа настройте параметрические слайдеры, позволяющие изменять входные данные в реальном времени и сразу видеть влияние на графическое представление.

Вопрос-ответ:

Как в Mathcad задать систему из нескольких уравнений для одновременного решения?

Для создания системы уравнений в Mathcad нужно записать каждое уравнение на отдельной строке и объединить их в одно выражение с помощью фигурных скобок { }. Например, если у вас есть уравнения x + y = 5 и 2x — y = 3, то в Mathcad их можно записать так: {x + y = 5, 2x — y = 3}. Затем, чтобы решить систему, используйте функцию `solve` или `FindRoot`, указав переменные, которые нужно найти. Это позволит получить значения всех переменных, удовлетворяющие заданным уравнениям.

Можно ли в Mathcad решить систему нелинейных уравнений? Какие функции для этого использовать?

Да, Mathcad позволяет решать системы нелинейных уравнений. Для этого обычно применяется функция `FindRoot`, которая ищет численное решение системы. Важно задать начальные приближения для переменных, чтобы алгоритм успешно сошёлся. В случае системы из нескольких уравнений, необходимо передать их как вектор уравнений и указать вектор переменных. Например, для системы {sin(x) + y^2 = 1, x^2 + y = 3} можно вызвать FindRoot, указав начальные значения x = 1 и y = 1.

Как правильно задать переменные в системе уравнений, чтобы Mathcad их корректно распознал?

В Mathcad переменные нужно определять без присвоения значений, чтобы они воспринимались как неизвестные. Если переменной уже присвоено значение, система будет воспринимать её как константу, и решение не получится. Лучше всего записать уравнения сразу с переменными, не вводя их через присваивание. Если нужно сбросить значение переменной, просто удалите присвоение или переопределите её в другом месте документа. Это позволит Mathcad корректно распознавать переменные в системе уравнений.

Каким образом можно проверить корректность решения системы уравнений в Mathcad?

Для проверки решения достаточно подставить найденные значения переменных обратно в исходные уравнения. В Mathcad это легко сделать, написав уравнения с уже подставленными значениями или использовав найденные переменные в выражениях. Если результат близок к нулю (для уравнений вида f(x)=0) или соответствует правой части, значит решение верное. Можно также проверить значения на различных приближениях, чтобы убедиться в стабильности результата.

Как задать систему уравнений с параметрами и найти решение при разных значениях параметров?

В Mathcad можно вводить параметры как отдельные переменные с присвоенными значениями. В системе уравнений вместо чисел используйте эти параметры. Для разных значений параметров просто меняйте их значения в отдельной ячейке. После этого пересчитайте решение системы, и Mathcad обновит результат. Такой подход удобен, если нужно проанализировать, как меняется решение при варьировании параметров. Можно также использовать таблицы или циклы для автоматизации поиска решений при множестве значений параметров.

Как задать несколько уравнений одновременно в Mathcad и связать их между собой?

В Mathcad для создания системы уравнений нужно записать каждое уравнение отдельно, используя оператор равенства. Затем все уравнения можно объединить в одну систему с помощью функции, например, ‘solve’ или использовать переменные, которые участвуют в нескольких уравнениях, чтобы связать их между собой. Для решения системы обычно применяется оператор решения, который принимает на вход набор уравнений и неизвестных. Таким образом, Mathcad позволяет работать с комплексными системами, сохраняя взаимосвязь между уравнениями и переменными.

Можно ли в Mathcad использовать численные методы для решения сложных систем уравнений, если аналитическое решение невозможно?

Да, Mathcad поддерживает численные методы для решения систем уравнений, что особенно полезно, когда аналитическое выражение решения трудно или невозможно получить. В таких случаях применяются встроенные функции, например, ‘find’ или ‘root’, которые ищут приближённые корни уравнений. Пользователь задаёт начальные приближения для неизвестных, а программа последовательно уточняет значения, минимизируя ошибки. Это позволяет эффективно решать нелинейные системы или уравнения с большим числом переменных, обеспечивая приемлемую точность результатов.