Программная среда Mathcad позволяет решать системы алгебраических и дифференциальных уравнений как численно, так и аналитически. Одним из ключевых преимуществ является возможность визуального отображения математических операций, что упрощает отладку и верификацию результатов.
Для решения системы уравнений в Mathcad применяются встроенные функции solve, find, root и операторов определения системы. При этом необходимо точно задать переменные, условия и начальные приближения (для численного метода). Пример численного решения: использование Given-Find в блоке уравнений позволяет получить корни даже сложных нелинейных систем.
Если требуется символьное решение, используется оператор = вместе с функцией solve. Однако стоит учитывать, что не все системы поддаются аналитическому решению. В таких случаях Mathcad автоматически предложит переход к численным методам.
При работе с уравнениями векторного или матричного типа важно соблюдать размерность и порядок записи. Mathcad чувствителен к типу переменных, поэтому рекомендуется использовать явное задание размерности и проверку единиц измерения через встроенные средства валидации.
Для систем дифференциальных уравнений Mathcad предлагает модуль ODE Solve, позволяющий решать задачи Коши с заданными начальными условиями. Удобный графический интерфейс позволяет отслеживать изменение решения при варьировании параметров в реальном времени.
Построение системы линейных уравнений в символьной форме

Для задания системы линейных уравнений в символьной форме в Mathcad необходимо использовать оператор := для определения уравнений и функцию solve или lsolve для поиска решения. Символьная форма предполагает применение точных выражений без численных подстановок.
Пример системы:
eq1: 3·x + 2·y — z = 1
eq2: 2·x — 2·y + 4·z = -2
eq3: -x + 0.5·y — z = 0
Уравнения следует записывать с использованием оператора Ctrl += для символьного равенства. Для символьного решения используется функция solve({eq1, eq2, eq3}, {x, y, z}). Она возвращает точное выражение решений без округлений.
Для удобства можно использовать вектор переменных:
vars := [x, y, z]
eqs := [eq1, eq2, eq3]
Вызов solve(eqs, vars) обеспечит компактность записи и повышает читаемость.
Важно: коэффициенты должны быть заданы явно. Использование неинициализированных переменных приведёт к неопределённости решения.
Использование оператора solve для численного решения
В Mathcad оператор solve применяется для численного решения систем нелинейных уравнений. Он используется совместно с блоком Given, в котором задаются условия системы. После определения уравнений и начальных приближений переменных, оператор solve возвращает численное значение корней.
Синтаксис:
Given уравнение1 уравнение2 ... solve(переменная1, переменная2, ...)
Пример:
Given x + y = 10 x^2 + y^2 = 58 solve(x, y)
В данном примере Mathcad численно решает систему и возвращает значения x и y, удовлетворяющие обоим уравнениям. Для корректной работы требуется предварительное задание начальных значений переменных в виде:
x := 1 y := 1
Без начальных приближений Mathcad не сможет найти решение. Рекомендуется выбирать значения, близкие к предполагаемому корню, особенно при наличии нескольких решений. Если система не имеет решения, оператор solve выдаёт сообщение об ошибке.
При работе с нелинейными системами рекомендуется использовать solve вместо root, поскольку solve может обрабатывать несколько переменных одновременно. Однако для систем с жёсткой зависимостью между уравнениями лучше использовать оператор find, поскольку он допускает больше гибкости в настройке алгоритма.
Для повышения точности можно использовать изменение параметров решения через панель Calculation Options, где доступна настройка максимального количества итераций и точности сходимости.
Задание начальных приближений для нелинейных систем
- Используйте графический анализ: постройте графики функций системы для визуального определения точек пересечения. Это особенно полезно при двух переменных, когда можно увидеть характер системы и выбрать начальные значения, близкие к точному решению.
- Вычислите значение каждой функции при предполагаемых начальных приближениях. Все выражения должны давать значения, близкие к нулю. Если хотя бы одна функция даёт резко отличающееся значение – приближение неподходящее.
- Учитывайте поведение производных. Если производные функций по переменным резко меняются в предполагаемой области – возможна нестабильность метода Ньютона. Предпочтительны такие приближения, где якобиан невырожден.
- Для систем с несколькими решениями запустите вычисления из различных точек. Это позволяет определить все корни и избежать сходимости к одному и тому же решению.
- Избегайте нулевых значений в начальных приближениях, если они входят в знаменатели или аргументы логарифмов, корней, арктангенсов и других функций с ограниченной областью определения.
В Mathcad начальные приближения задаются через ключевое слово guess внутри блока Given-Find или Given-Solve. Например:
x := 1
y := 1
Given
f₁(x, y) = 0
f₂(x, y) = 0
Find(x, y)
Если система не решается или выдаёт ошибку «no solution found», измените начальные значения. Протестируйте диапазон значений, чтобы определить область устойчивой сходимости.
Настройка единиц измерения при работе с уравнениями
Mathcad автоматически учитывает единицы измерения при вычислениях, что позволяет избежать ошибок, связанных с несогласованностью величин. Для корректной работы с системой уравнений важно задать физические величины с указанием единиц сразу при их определении. Например, переменной давления следует присваивать значение так: P := 101.3 kPa, а не просто P := 101.3.
При решении системы с переменными в разных единицах (например, длина в метрах, сила в ньютонах, масса в килограммах), необходимо обеспечить их совместимость. Mathcad приведет все значения к единообразной системе, но если задать единицы неявно или пропустить их, результат может быть искажен.
Чтобы изменить систему единиц по умолчанию, откройте вкладку Math → Units и выберите нужную систему (SI, US Customary и др.). Это повлияет на отображение результатов и интерпретацию вводимых данных.
Для отображения результата в конкретных единицах используйте оператор →. Пример: x := 5 m, затем x → cm отобразит результат в сантиметрах. Это особенно важно при работе с результатами решения уравнений, где требуется контроль над выходными единицами.
Если система уравнений содержит переменные без единиц, Mathcad интерпретирует их как безразмерные. Чтобы избежать неоднозначности, желательно явно указывать единицы даже для промежуточных переменных, особенно если они участвуют в расчетах с физическими величинами.
Ошибки, связанные с несовместимостью единиц, легко обнаруживаются: Mathcad подсветит выражение красным и выведет сообщение об ошибке. В этом случае проверьте, чтобы все входные данные и переменные имели согласованные единицы, и при необходимости приведите их к общей системе вручную.
Применение функции root для поиска конкретного решения

Функция root в Mathcad позволяет найти единственное решение нелинейной системы уравнений при заданных начальных приближениях. Это критически важно, когда система имеет несколько решений, и требуется определить конкретное из них.
Синтаксис: root(f(x), x, x₀), где f(x) – выражение или система уравнений, x – переменная, а x₀ – начальное приближение. Для системы уравнений используется вектор переменных и вектор начальных значений.
Пример: необходимо найти решение системы:
x² + y² = 10 x - y = 1
Объявите переменные x и y как вектор v := [x, y], составьте вектор уравнений F(v) := [v₀² + v₁² — 10, v₀ — v₁ — 1], затем примените root(F(v), v, [2,1]). Mathcad вычислит решение, соответствующее указанному приближению.
Корректный выбор начального значения x₀ позволяет управлять результатом и получать нужный корень даже при наличии нескольких. При недостаточно близком приближении функция может не сойтись – тогда рекомендуется визуализировать функцию или использовать solve block с оператором guess для уточнения.
Функция root применяется только для численного решения; она не возвращает аналитическое выражение. Ее следует использовать, когда символические методы неприменимы или дают множество решений без указания конкретного.
Визуализация решений с помощью графиков в Mathcad
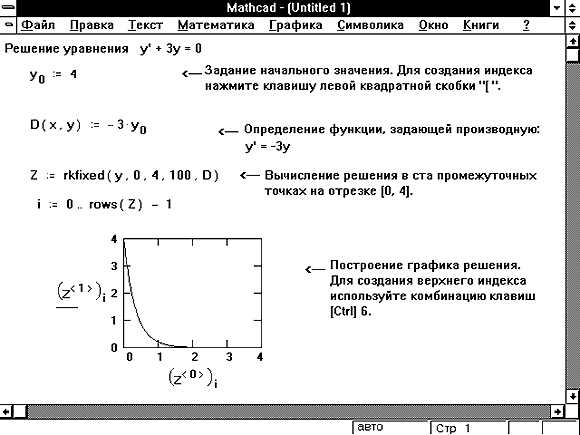
Для визуального анализа решений системы уравнений в Mathcad применяется построение графиков функций, полученных в результате вычислений. После решения системы необходимо определить диапазон переменных, чтобы график отражал интересующую область. Это делается через задание интервалов с помощью оператора диапазона, например, x := 0, 0.1 .. 10.
Для двумерной визуализации используют функцию plot, задавая оси X и Y через вычисленные значения переменных. Важно проверять корректность диапазона, чтобы избежать сжатия или искажения графика. Рекомендуется использовать команды zoom и масштабирование для точного рассмотрения критических участков.
При решении систем с несколькими переменными оптимально использовать параметрические графики, отображающие зависимости в виде кривых или поверхностей. Mathcad поддерживает построение 3D-графиков с помощью функции surface, где параметры задаются через матрицы значений. Это позволяет увидеть пересечения и точки совпадения решений.
Для наглядности стоит добавлять подписи к осям и легенду через функции label и legend, что облегчает интерпретацию результатов. Важным элементом является выделение точек решения с помощью маркеров – их можно задать через параметры plot с указанием типа и цвета символов.
Mathcad позволяет строить несколько графиков на одном полотне для сравнения вариантов решений или визуализации систем с параметрами. Для этого используют оператор overlay, который объединяет несколько функций в одном окне.
При сложных системах с неявными уравнениями рекомендуется предварительно вычислять значения функций на сетке точек, затем создавать графики по полученным массивам, что снижает ошибки построения и повышает точность отображения.
Проверка корректности введённых уравнений и переменных
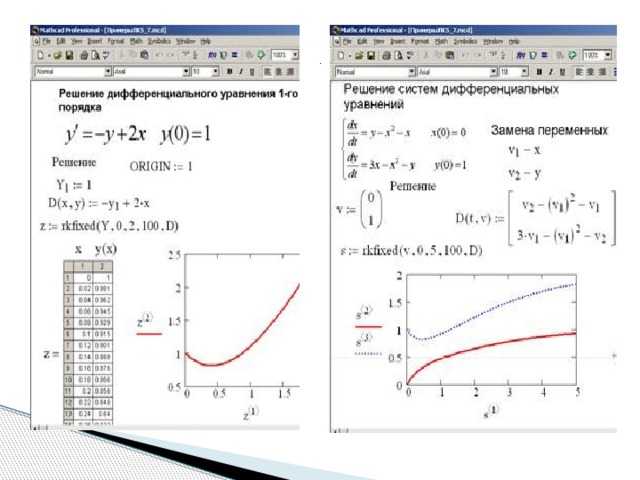
Перед решением системы уравнений в Mathcad необходимо убедиться в правильности формулировки уравнений и корректности заданных переменных. Ошибки на этом этапе приводят к неверным результатам или невозможности вычислений.
- Проверка синтаксиса уравнений: Mathcad требует строгого соблюдения синтаксиса. Следует проверить отсутствие лишних или пропущенных скобок, корректность знаков операций и равенств. Особенно важно, чтобы все выражения имели смысл как математические формулы.
- Проверка имен переменных: Переменные не должны совпадать с зарезервированными именами функций или констант Mathcad. Рекомендуется использовать уникальные, осмысленные имена без пробелов и специальных символов.
- Проверка типовых ошибок:
- Отсутствие значений для переменных, которые должны быть заданы заранее.
- Использование в уравнениях переменных с неоднозначными типами (например, числовых и векторных).
- Несоответствие размерностей при работе с матрицами и векторами.
- Использование встроенных функций проверки: Mathcad позволяет выделять ошибки подсветкой. При наличии ошибок в уравнении появляются предупреждающие знаки, наводя курсор на которые, можно получить описание проблемы.
- Тестирование с известными значениями: Для сложных систем полезно подставить в уравнения фиксированные числовые значения переменных, чтобы проверить корректность вычислений и адекватность формул.
- Обозначение переменных с начальным значением: В системах нелинейных уравнений указывать начальные приближения к переменным – это критично для сходимости метода решения.
Пошаговая проверка и корректировка уравнений перед запуском решения снижает вероятность ошибок и экономит время на отладку моделей в Mathcad.
Решение параметрических систем с использованием ползунков
Ползунки в Mathcad обеспечивают интерактивное изменение параметров системы уравнений, позволяя анализировать влияние параметров на решения в реальном времени. Для настройки ползунка необходимо задать диапазон изменения и шаг, которые соответствуют области интереса задачи. Например, если параметр a варьируется от 0 до 10 с шагом 0.1, создайте ползунок с такими значениями, чтобы обеспечить плавное и точное исследование.
При формулировке системы с параметрами используйте имена переменных, связываемые с ползунками. Это позволит автоматизировать пересчет решений при каждом изменении положения ползунка. В Mathcad рекомендуется применять встроенную функцию solve для численного решения с учетом текущих значений параметров, что исключает необходимость повторного ввода системы вручную.
Для удобства визуализации результатов рекомендуется строить графики решений, привязанные к ползункам. Это дает возможность наблюдать динамику решения при изменении параметра и выявлять критические точки, например, точки бифуркации или переходы между режимами. Важный момент – ограничение области определения ползунка таким образом, чтобы решения системы оставались корректными и не приводили к ошибкам вычислений.
При работе с несколькими параметрами рекомендуется создавать отдельные ползунки и использовать функцию vectorize для обработки массива параметров, что ускоряет вычисления и упрощает настройку. В случае сложных систем рекомендуется разбивать задачу на этапы, последовательно изменяя один параметр, сохраняя остальные фиксированными, чтобы избежать неопределенности в решениях.
Поддержание чистоты и понятности рабочего листа важно для быстрого поиска и устранения ошибок. Рекомендуется сопровождать каждый ползунок короткими комментариями, указывающими физический смысл параметра и границы допустимых значений. Такой подход повышает качество анализа и делает результаты воспроизводимыми.
Вопрос-ответ:
Как в Mathcad задать систему уравнений для последующего решения?
В Mathcad система уравнений задаётся через запись каждого уравнения с использованием переменных и операторов. Важно правильно оформить уравнения с учётом синтаксиса программы, например, использовать двоеточие для определения переменных и знак равенства для уравнивания выражений. После этого можно применять функцию решения систем, указывая уравнения и переменные, которые нужно найти.
Какие методы решения систем уравнений поддерживает Mathcad?
Mathcad умеет решать системы как линейных, так и нелинейных уравнений. Для линейных систем чаще применяется аналитический метод с помощью функции линейного решения, а для нелинейных — численные методы, такие как метод Ньютона. Выбор метода зависит от вида системы и её сложности, и Mathcad автоматически подбирает подходящий алгоритм.
Можно ли в Mathcad решать системы с большим числом уравнений и переменных?
Да, Mathcad позволяет работать с системами различного размера — от нескольких уравнений до больших наборов с десятками переменных. Однако при увеличении объёма системы время решения может возрасти, а точность зависит от численных методов. Для больших систем рекомендуется внимательно проверять корректность постановки задачи и исходных данных.
Как задать начальные приближения для решения нелинейной системы в Mathcad?
Для численного решения нелинейных систем важно указать начальные приближения, чтобы программа могла начать итерационный процесс. В Mathcad это делается через параметры функции решения: задаются стартовые значения переменных в виде вектора или набора чисел. Правильно выбранные начальные приближения помогают избежать сходимости к неправильным корням или к неустойчивым решениям.
Какие ошибки наиболее распространены при решении систем уравнений в Mathcad и как их избежать?
Часто встречаются ошибки синтаксиса при вводе уравнений, неправильное определение переменных и несоответствие размеров матриц. Ещё одна частая проблема — неверно указанные начальные условия при численном решении, что ведёт к отсутствию сходимости. Чтобы минимизировать ошибки, важно внимательно проверять формат уравнений, корректность переменных и разумность начальных значений.
Как в Mathcad можно задать и решить систему нелинейных уравнений?
В Mathcad система нелинейных уравнений задаётся в виде набора выражений, каждое из которых приравнивается к нулю. Для решения используют встроенную функцию `find`, которая позволяет найти корни системы. Важно задать начальное приближение для переменных, так как метод решения итеративный. Например, для системы из двух уравнений нужно определить две переменные и затем вызвать функцию `find` с массивом уравнений и начальным приближением. Mathcad автоматически подберёт значения, при которых все уравнения будут выполнены с нужной точностью.