Как в mathematica wolfram построить график

Mathematica Wolfram предоставляет мощный набор инструментов для визуализации данных и функций. Чтобы эффективно создавать графики, важно понять базовые команды и параметры, управляющие отображением. В этой статье представлена конкретная последовательность действий, позволяющая быстро переходить от простого построения к более сложным визуализациям.

Начать стоит с использования функции Plot, которая подходит для построения графиков функций одной переменной. При вводе Plot[f[x], {x, a, b}] задается интервал, на котором строится график. Важным моментом является правильный выбор диапазона и опций, например, PlotRange для ограничения видимой области или PlotStyle для настройки внешнего вида линии.

Для отображения нескольких функций на одном графике используется синтаксис Plot[{f[x], g[x]}, {x, a, b}]. В дополнение к базовым командам стоит освоить функции ParametricPlot для параметрических кривых и ListPlot для визуализации дискретных наборов данных. Каждый тип графика имеет свои особенности и ключевые параметры, которые подробно рассмотрены в дальнейшем.

Как создать базовый график функции с помощью Plot

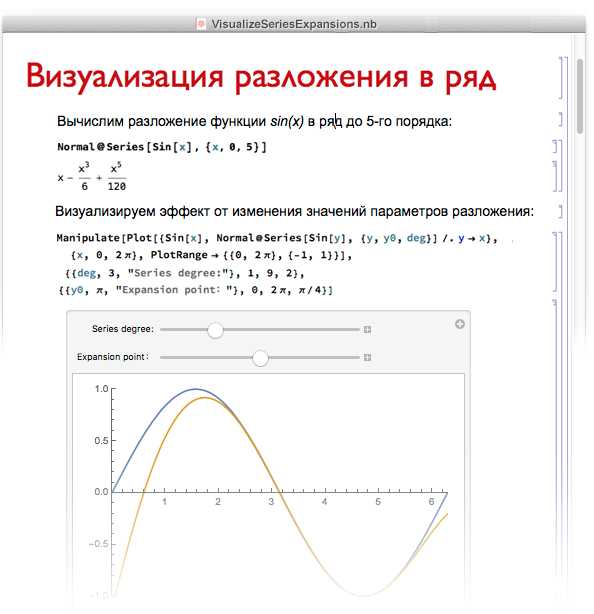
Для построения графика функции в Mathematica используется команда Plot. Синтаксис: Plot[функция, {переменная, начало, конец}]. Например, Plot[Sin[x], {x, 0, 2 Pi}] построит график синуса на интервале от 0 до 2π.

Входной параметр функция задается в виде выражения, зависящего от переменной. Диапазон переменной указывается в фигурных скобках, где начало и конец – числовые значения.

Команда автоматически создает масштабированные оси и сетку по умолчанию. Для изменения интервала достаточно подставить другие границы, например: Plot[x^2, {x, -3, 3}].

Если необходимо отобразить несколько функций одновременно, следует использовать список, например: Plot[{Sin[x], Cos[x]}, {x, 0, 2 Pi}]. Каждая функция будет изображена своим цветом.

Для точной настройки внешнего вида графика рекомендуются параметры PlotStyle (цвет, толщина линии), PlotRange (область отображения по осям) и AxesLabel (подписи осей).

Пример с настройками: Plot[Sin[x], {x, 0, 2 Pi}, PlotStyle -> Red, PlotRange -> {-1, 1}, AxesLabel -> {"x", "sin(x)"}].

Запуск команды в блоке ввода Mathematica мгновенно отобразит график, готовый для дальнейшего анализа или сохранения.

Настройка внешнего вида графика: цвета, толщины и стили линий

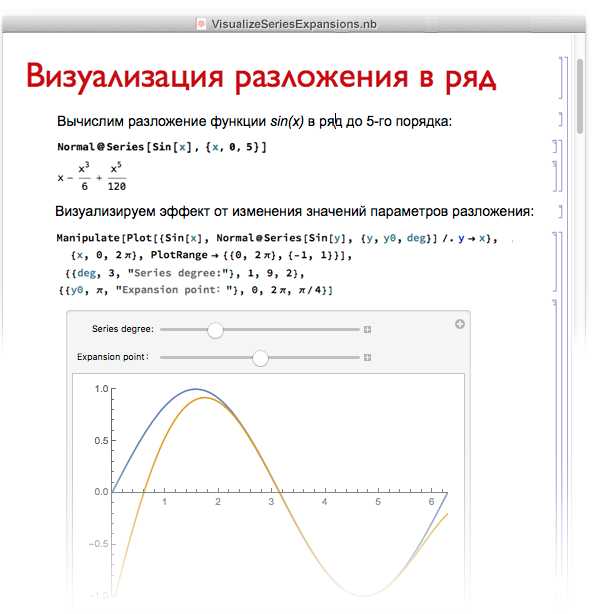
Толщину линии регулируют функцией Thickness, которая принимает значение от 0 до 1, где 0.01–0.005 подходит для тонких линий, а 0.02–0.03 – для выделенных. Например, PlotStyle -> {Red, Thickness[0.015]} создаст красную линию средней толщины.

Стиль линии задаётся с помощью Directive и Dashed или Dotted. Параметр Dashed принимает список чисел, задающих длину штрихов и пробелов: Dashed[{0.02, 0.01}] – короткие штрихи и пробелы. Для точечной линии используют Dotted, а для комбинированных эффектов – Directive[Blue, Thickness[0.01], Dashed[{0.03, 0.015}]].

Для множественных графиков PlotStyle принимает список стилей: PlotStyle -> {{Red, Thickness[0.015]}, {Blue, Dashed}} применит разные параметры к каждой линии.

Изменение цвета осей и сетки выполняется через AxesStyle и GridLinesStyle с аналогичными настройками цвета и толщины.

Для комплексной настройки линий удобно использовать Directive, комбинируя несколько параметров. Это обеспечивает точное управление внешним видом без необходимости повторять код.

Построение нескольких функций на одном графике с Plot и Show

В Mathematica для отображения нескольких функций на одном графике удобнее всего использовать сочетание Plot и Show. Первый шаг – построить отдельные графики функций с помощью Plot, затем объединить их командой Show.

Для построения нескольких функций одновременно можно передать список функций в Plot, например: Plot[{Sin[x], Cos[x]}, {x, 0, 2 Pi}]. Однако для тонкой настройки стилей каждого графика лучше использовать несколько вызовов Plot с параметрами оформления, после чего объединить их.

Пример построения двух графиков с разными цветами и толщиной линий:

p1 = Plot[Sin[x], {x, 0, 2 Pi}, PlotStyle -> {Red, Thick}];
p2 = Plot[Cos[x], {x, 0, 2 Pi}, PlotStyle -> {Blue, Dashed}];
Show[p1, p2]

При использовании Show важно, чтобы области построения (диапазоны по осям) совпадали или были совместимы, иначе часть графиков может оказаться вне отображаемой области. Это регулируется параметрами PlotRange.

Для сохранения легенды на комбинированном графике рекомендуется использовать пакет PlotLegends или добавлять легенду вручную с помощью Legended и LineLegend.

Если требуется объединить графики с разными функциями отображения (например, точечные данные и линии), Show объединит их корректно, сохраняя свойства каждого элемента.

Добавление подписей и аннотаций к графикам в Mathematica

Для добавления подписей к осям графика используйте параметры AxesLabel и PlotLabel. Например, Plot[Sin[x], {x, 0, 2 Pi}, AxesLabel -> {"x", "sin(x)"}, PlotLabel -> "График функции sin(x)"] создаст график с подписями осей и заголовком.

Для позиционирования и форматирования подписей применяйте функцию Style. Пример: AxesLabel -> {Style["x", Red, Italic], Style["sin(x)", Blue, Bold]}.

Аннотации внутри графика вставляют через Epilog. Это список графических примитивов, который накладывается поверх графика. Например, Epilog -> {Text["Максимум", {Pi/2, 1}, {0, -1}]} добавит текстовую метку в точке максимума синуса.

Для динамического вычисления координат аннотаций удобно использовать переменные из области построения или результаты вычислений. Например, With[{max = {Pi/2, 1}}, Plot[Sin[x], {x, 0, 2 Pi}, Epilog -> {Text["Максимум", max, {0, -1}]}]].

Можно добавлять стрелки и линии с помощью Arrow и Line в списке Epilog. Пример: Epilog -> {Arrow[{{Pi/2, 0.5}, {Pi/2, 1}}]} добавит стрелку к максимуму.

Для автоматического масштабирования подписей рекомендуются относительные координаты, например, используя Scaled. Текст Text["Среднее", Scaled[{0.7, 0.5}] разместит подпись в 70% ширины и 50% высоты графика.

Чтобы добавить несколько подписей и аннотаций, объедините их в список внутри Epilog -> {…}. Каждый элемент может быть текстом, стрелкой или фигурой.

Подписи осей можно дополнительно настроить через Ticks с параметром Style для выделения определённых меток.

Использование ListPlot для визуализации дискретных данных

В Mathematica функция ListPlot предназначена для построения графиков по набору точек, заданных в виде списка координат. Для дискретных данных исходные значения задаются списком чисел или пар {x, y}. Например, ListPlot[{1, 3, 2, 5, 4}] создаст график с точками на позициях по оси X, соответствующих индексам элементов, и значениями по оси Y из списка.

Если требуется точный контроль по осям, данные задают в формате пар: ListPlot[{{x1, y1}, {x2, y2}, ...}]. Такой подход удобен при неравномерном распределении точек по оси X.

Для улучшения читаемости и визуального выделения точек рекомендуется использовать опцию PlotStyle, например, PlotStyle -> Red окрашивает точки в красный цвет. Размер точек регулируется через PlotMarkers, например, PlotMarkers -> {"●", 12} задаёт маркер размером 12.

Чтобы соединить точки линиями, добавляют опцию Joined -> True. Это удобно для анализа трендов в дискретных наборах данных.

Важный параметр – Frame -> True заменяет стандартные оси рамкой, что улучшает восприятие координат. Настройка подписей осей доступна через FrameLabel -> {"X", "Y"}.

Пример построения графика с цветными маркерами и соединением точек:

ListPlot[
{{1, 2}, {2, 3}, {3, 5}, {4, 4}},
Joined -> True,
PlotStyle -> Blue,
PlotMarkers -> {"\[FilledCircle]", 10},
Frame -> True,
FrameLabel -> {"Время", "Значение"}
]

Для больших наборов данных целесообразно использовать опцию PerformanceGoal -> "Speed" для ускорения отрисовки без значительной потери качества.

При работе с дискретными данными стоит избегать автоматического сглаживания кривых и лишних интерполяций. Настройка параметра InterpolationOrder -> 0 гарантирует, что между точками не будет добавлено промежуточных значений.

Для анализа категориальных данных в формате {категория, значение} можно преобразовать категории в числовые индексы и подписать ось X вручную через Ticks или FrameTicks, чтобы сохранить точную семантику визуализации.

Сохранение и экспорт графиков из Mathematica в разные форматы

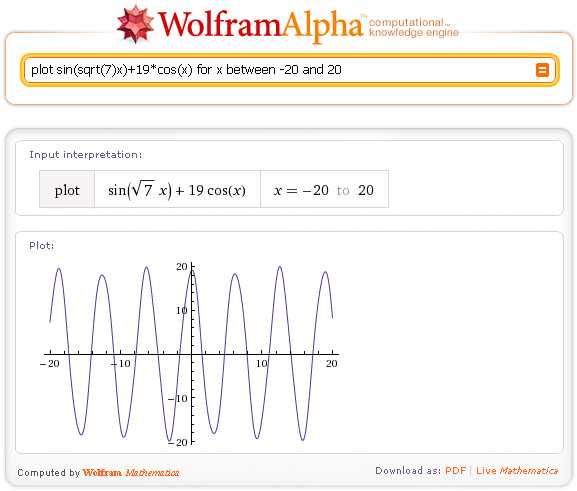
В Mathematica для сохранения графиков применяются функции, позволяющие экспортировать изображения в множество форматов с сохранением качества и настроек визуализации.

1. Экспорт в стандартные графические форматы:
   • Используйте функцию Export["имя_файла.формат", график]. Например, Export["plot.png", plot] сохранит график в PNG.
   • Поддерживаются форматы: PNG, JPEG, TIFF, BMP, GIF.
   • Для векторной графики рекомендуется формат SVG или PDF, позволяющие масштабировать изображение без потери качества: Export["plot.svg", plot].
2. Настройка качества и разрешения:
   • Для растровых форматов можно указать разрешение с помощью опции "ImageResolution", например, Export["plot.png", plot, "ImageResolution" -> 300] для 300 dpi.
   • Для PDF и SVG разрешение не влияет, поскольку это векторные форматы.
3. Экспорт нескольких графиков:
   • Для серии графиков экспортируйте список: Export["plots.pdf", {plot1, plot2, plot3}].
   • Для GIF-анимации используйте: Export["animation.gif", список_кадров, "DisplayDurations" -> 0.1].
4. Сохранение графика с сохранением интерактивности:
   • Для сохранения интерактивных элементов используйте формат CDF через Export["interactive.cdf", график].
   • Файлы CDF можно просматривать с помощью Wolfram CDF Player.
5. Дополнительные рекомендации:
   • Перед экспортом убедитесь, что график полностью отрисован (используйте Show[график]).
   • Для автоматизации экспорта в разных форматах используйте цикл с функцией Export.
   • В случае сложных графиков с прозрачными слоями лучше использовать форматы PNG или TIFF с поддержкой прозрачности.

Вопрос-ответ:

Как в Mathematica построить простой график функции?

Для построения базового графика функции в Mathematica используется команда Plot. Например, чтобы изобразить график функции y = x^2 на промежутке от -2 до 2, нужно написать: Plot[x^2, {x, -2, 2}]. После выполнения команды появится окно с изображением кривой. Такой способ подходит для большинства стандартных функций.

Можно ли одновременно построить несколько графиков на одном изображении? Как это сделать?

Да, Mathematica позволяет отображать несколько функций на одном графике. Для этого в функцию Plot передается список выражений вместо одного. Например, Plot[{Sin[x], Cos[x]}, {x, 0, 2 Pi}] нарисует кривые синуса и косинуса на одном полотне. Дополнительно можно настроить цвета и легенду, используя параметры PlotStyle и PlotLegends.

Какие есть способы изменить внешний вид графика, например цвет, толщину линий и подписи осей?

В Mathematica для настройки графика применяются различные опции. Параметр PlotStyle позволяет задать цвет и толщину линий, например PlotStyle -> {Red, Thick}. Подписи осей меняются с помощью AxesLabel -> {«x», «y»}. Чтобы добавить заголовок, используется PlotLabel -> «Название графика». Такой подход помогает сделать визуализацию более информативной и понятной.

Как построить график функции с несколькими переменными, например трехмерный график?

Для построения трехмерных графиков в Mathematica применяется функция Plot3D. Например, Plot3D[Sin[x y], {x, -3, 3}, {y, -3, 3}] создаст поверхность, зависящую от двух переменных x и y. Эта команда позволяет визуализировать сложные зависимости и поверхности в трехмерном пространстве.

Как сохранить полученный график в файл с нужным форматом и разрешением?

Для экспорта графика используется команда Export. После построения графика, например, plot = Plot[Sin[x], {x, 0, 2 Pi}], можно сохранить изображение в файл так: Export[«путь/к/файлу.png», plot]. Формат файла определяется по расширению (.png, .jpg, .pdf и др.). Кроме того, в Export можно указать параметры качества и размера, чтобы получить изображение с нужным разрешением.

Как построить простой график функции в Mathematica?

Для создания базового графика функции в Mathematica используется команда Plot. Например, чтобы построить график функции y = x^2 на интервале от -3 до 3, достаточно написать: Plot[x^2, {x, -3, 3}]. Эта команда создаст изображение параболы. Можно менять вид графика, добавлять подписи и изменять цвет с помощью дополнительных опций.