Wolfram Mathematica – это не просто система для символьных вычислений, а мощная среда для построения моделей, анализа данных и автоматизации вычислительных задач. Чтобы эффективно использовать её возможности, необходимо понимать не только синтаксис языка Wolfram Language, но и логику, лежащую в основе его функционального подхода.
Каждая задача – от построения графиков до решения дифференциальных уравнений – реализуется через чёткую комбинацию функций, списков и правил. Например, визуализация функции реализуется вызовом Plot[f[x], {x, a, b}], где важно не забывать об обязательном указании диапазона переменной. Пропуск этого шага приведёт к немедленной ошибке выполнения.
Реализация численного решения задачи сводится к вызову NDSolve, где особое внимание стоит уделить формату ввода уравнений и начальных условий. Неправильный синтаксис {y'[x] == -y[x], y[0] == 1} может привести к неинформативному сообщению об ошибке, если, например, указать y’[x] = -y[x].
Работа с данными требует чёткого понимания структуры списков. Для вычисления среднего значения по столбцу в CSV-файле, импортируемом с помощью Import[«file.csv»], используется цепочка Mean /@ Transpose[data]. Ошибки здесь возникают чаще всего из-за попытки применять Mean к неправильному уровню вложенности.
Для продуктивной работы важно использовать встроенные справочные механизмы: ? и Information[«функция»]. Они не только показывают синтаксис, но и предлагают примеры, которые можно сразу протестировать и адаптировать под конкретную задачу.
Как построить график функции с заданным диапазоном и стилем
Для построения графика функции в Mathematica с указанием конкретного диапазона и оформления используется функция Plot. Например, чтобы отобразить синус на интервале от 0 до 2π, выполните:
Plot[Sin[x], {x, 0, 2 Pi}]
Чтобы изменить стиль линии, добавьте опции: PlotStyle для цвета и толщины, Dashed или Dotted – для типа линии. Пример с красной пунктирной линией толщиной 2:
Plot[Sin[x], {x, 0, 2 Pi}, PlotStyle -> {Red, Dashed, Thickness[0.005]}]
Для одновременного отображения нескольких функций с индивидуальными стилями используйте список:
Plot[{Sin[x], Cos[x]}, {x, 0, 2 Pi}, PlotStyle -> {{Blue, Thick}, {Green, Dotted}}]
Чтобы задать ограничение по значениям осей, применяйте опцию PlotRange. Пример для отображения области по y от -0.5 до 1:
Plot[Sin[x], {x, 0, 2 Pi}, PlotRange -> {-0.5, 1}]
Для настройки сетки используйте GridLines -> Automatic или задайте вручную:
Plot[Sin[x], {x, 0, 2 Pi}, GridLines -> {{π, 2 π}, {-1, 0, 1}}]
Подписи и оформление осей задаются через AxesLabel и LabelStyle. Например:
Plot[Sin[x], {x, 0, 2 Pi}, AxesLabel -> {"x", "sin(x)"}, LabelStyle -> {FontSize -> 14}]
Для экспорта графика используйте Export["путь/файл.png", график]. Например:
Export["~/Desktop/sinplot.png", Plot[Sin[x], {x, 0, 2 Pi}]]
Как решить систему линейных уравнений с параметрами
Для решения системы линейных уравнений с параметрами в Wolfram Mathematica используйте функцию Solve или Reduce. Важно задать параметры как символы, чтобы сохранить общую форму решения.
- Определите переменные и параметры. Например,
{x, y}– переменные,a, b– параметры. - Запишите уравнения в виде списка. Пример:
{a x + y == 1, x - b y == 2}. - Выполните команду
Solve:Solve[{a x + y == 1, x - b y == 2}, {x, y}]Это даст общее решение при произвольных значениях параметров, если система совместна.
- Для анализа условий существования решения используйте
Reduce:Reduce[{a x + y == 1, x - b y == 2}, {x, y}]Этот подход покажет, при каких значениях параметров решение существует и является единственным.
- Чтобы исключить вырожденные случаи (например, деление на ноль), явно задайте ограничения:
Reduce[{a x + y == 1, x - b y == 2} && a != 0 && b != 1, {x, y}] - Для получения матричной формы системы используйте
LinearSolve:LinearSolve[{{a, 1}, {1, -b}}, {1, 2}]Работает только при заданных значениях параметров. С символьными параметрами используйте
Inverse:Inverse[{{a, 1}, {1, -b}}].{1, 2}
Для проверки особых случаев (например, несовместность или бесконечное число решений), используйте SolveAlways или FindInstance.
Как провести символьное дифференцирование и упростить результат
Для символьного дифференцирования в Wolfram Mathematica используется функция D. Например, чтобы найти производную функции f[x_] := Sin[x^2] + x*Exp[x] по переменной x, введите:
D[Sin[x^2] + x*Exp[x], x]
Результат будет выражением в неупрощённой форме. Для его упрощения используйте функцию FullSimplify:
FullSimplify[D[Sin[x^2] + x*Exp[x], x]]
Если требуется упростить производную по заданным условиям, добавьте их в виде второго аргумента:
FullSimplify[D[Sin[x^2] + x*Exp[x], x], x > 0]
Для упрощения без глубокой алгебраической трансформации используйте Simplify. Она быстрее и менее агрессивна, чем FullSimplify.
Если требуется многократное дифференцирование, укажите степень производной вторым аргументом:
D[Sin[x^2] + x*Exp[x], {x, 2}]
Для дифференцирования по нескольким переменным используйте список:
D[x^2*y + Log[y], {x, 1}, {y, 1}]
Комбинируя D с Simplify или FullSimplify, можно получить компактные и пригодные к анализу выражения. Всегда проверяйте результат на предмет возможного упрощения, особенно при работе с вложенными функциями и тригонометрией.
Как импортировать и обрабатывать таблицу данных из Excel
Для загрузки Excel-файла используйте функцию Import с указанием полного пути к файлу и формата:
data = Import["C:\\путь\\к\\файлу.xlsx", {"Sheets", "Лист1"}]Если требуется загрузить только определённый диапазон, используйте опцию "DataRange":
data = Import["C:\\путь\\к\\файлу.xlsx", {"Sheets", "Лист1"}, "DataRange" -> {{2, 10}, {1, 4}}]Для первичной проверки структуры данных:
Dimensions[data]– размеры таблицыHead /@ data[[1]]– типы данных в первой строке
Для очистки данных от заголовков и пустых строк используйте:
cleanData = Select[data[[2 ;;]], FreeQ[#, ""] &]Для приведения строк в числа:
numericData = ToExpression /@ cleanDataЕсли требуется извлечь столбец по номеру:
column3 = numericData[[All, 3]]Для фильтрации строк по условию:
filtered = Select[numericData, #[[2]] > 100 && #[[4]] == "да" &]Для визуализации данных:
ListPlot[column3]– график значений третьего столбцаHistogram[column3]– гистограмма распределения
Сохранить обработанные данные обратно в Excel:
Export["C:\\путь\\к\\новому_файлу.xlsx", numericData]Как задать и визуализировать трехмерную поверхность
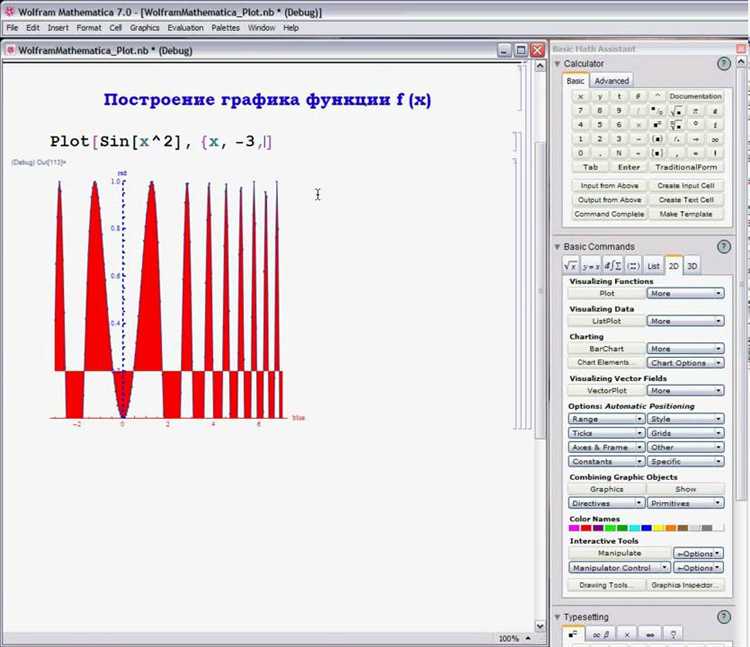
Для построения трехмерной поверхности в Wolfram Mathematica используется функция Plot3D. Она принимает выражение от двух переменных и диапазоны изменения каждой переменной.
Пример построения поверхности: Plot3D[Sin[x y], {x, -3, 3}, {y, -3, 3}]. Это создаёт график функции Sin[x y] в области x ∈ [-3, 3], y ∈ [-3, 3].
Для управления детализацией используется параметр PlotPoints. Например, Plot3D[Sin[x y], {x, -3, 3}, {y, -3, 3}, PlotPoints -> 100] увеличивает количество точек, повышая качество визуализации.
Настройка внешнего вида доступна через параметры: Mesh -> None убирает сетку, ColorFunction -> "Rainbow" окрашивает поверхность по высоте, Lighting -> "Neutral" отключает блики.
Для построения параметрических поверхностей используется ParametricPlot3D. Пример: ParametricPlot3D[{u Cos[v], u Sin[v], u^2}, {u, 0, 2}, {v, 0, 2 Pi}]. Это создаёт параболоид в цилиндрических координатах.
Цветовая карта может зависеть от параметров: ColorFunction -> Function[{u, v, x, y, z}, ColorData["ThermometerColors"][z]] позволяет задавать цвета вручную в зависимости от координат.
Для прозрачности используется PlotStyle -> Opacity[0.6]. Объединение нескольких графиков возможно через Show: Show[graf1, graf2].
Как автоматизировать повторяющиеся вычисления с помощью модуля
В Wolfram Mathematica модуль (Module) позволяет создавать локальные переменные и упаковывать вычисления в независимую функцию. Это идеально подходит для автоматизации повторяющихся задач с вариативными параметрами. Для создания модуля используйте конструкцию:
Module[{локальные_переменные}, тело_вычислений]
Локальные переменные существуют только внутри модуля, что исключает конфликт с глобальными именами и облегчает многократный вызов. Например, если необходимо вычислить интеграл с параметром, можно написать:
intCalc[x_] := Module[{res}, res = Integrate[Sin[a x], {a, 0, 1}]; res]
При каждом вызове intCalc с новым аргументом создаётся отдельная область с переменной res, исключая ошибки из-за сохранения значений между вычислениями.
Для повышения эффективности можно использовать модуль в сочетании с функциями кеширования. Например, добавьте проверку существующего результата в локальной памяти модуля, чтобы избежать повторных затратных вычислений.
В случае работы с итерациями, модуль позволяет хранить промежуточные состояния в локальных переменных, упрощая написание циклов и рекурсий без риска воздействия на внешнюю среду.
Также рекомендуют придерживаться компактного оформления тела модуля, минимизируя внешние зависимости и вводя параметры явно в список локальных переменных, что улучшает читаемость и отладку.
Использование Module в качестве контейнера вычислений – базовый приём для создания автономных, повторно используемых компонентов с предсказуемым поведением, что особенно важно в сложных и масштабных проектах на Mathematica.
Как экспортировать результаты вычислений в формат PDF или PNG
Для экспорта результатов в Wolfram Mathematica используется функция Export. Она позволяет сохранить любой выраженный результат в файлы различных форматов, в том числе PDF и PNG.
Чтобы экспортировать график или любое выражение в PDF, достаточно вызвать:
Export["имя_файла.pdf", выражение]
Для сохранения изображения (графика, фрагмента визуализации) в PNG формат используйте:
Export["имя_файла.png", выражение]
Если требуется контролировать разрешение изображения, добавьте опцию "ImageResolution":
Export["имя_файла.png", выражение, "ImageResolution" -> 300]
Для сложных отчетов с несколькими результатами лучше создавать объект Notebook или использовать Grid с данными, а затем экспортировать его в PDF:
Export["отчет.pdf", Notebook[{Cell["Заголовок", "Section"], Cell[BoxData@ToBoxes[выражение], "Output"]}] ]
При экспорте в PDF учитывайте, что векторные объекты сохраняются с высоким качеством, а растровые изображения – с ограничениями разрешения. Для сохранения именно визуализации, сгенерированной на экране, применяйте экспорт в PNG.
Для проверки содержимого файла после экспорта используйте SystemOpen["имя_файла.pdf"] или SystemOpen["имя_файла.png"].
Вопрос-ответ:
Как загрузить и импортировать данные из файла CSV в Wolfram Mathematica?
Чтобы загрузить данные из CSV-файла, используется функция Import с указанием пути к файлу и формата «CSV». Например, Import[«путь/к/файлу.csv», «CSV»] вернёт список списков, где каждый вложенный список соответствует строке из файла. После этого можно обрабатывать данные как обычные списки в Mathematica.
Каким образом создать график функции с несколькими параметрами и задать диапазон для каждого параметра?
Для построения графика функции с несколькими параметрами используется Plot3D или ContourPlot, если функция зависит от двух переменных. Например, Plot3D[f[x, y], {x, xmin, xmax}, {y, ymin, ymax}] построит трёхмерный график функции f на заданных интервалах. При необходимости параметр можно задавать как дополнительную переменную и исследовать поведение функции.
Как в Wolfram Mathematica написать цикл, который будет выводить значения функции для последовательных целых чисел?
В Mathematica чаще применяют функциональные конструкции, но если нужен цикл, можно использовать Do. Например, Do[Print[f[n]], {n, 1, 10}] выведет значения функции f при n от 1 до 10. Также удобно использовать Table[f[n], {n, 1, 10}], чтобы получить список результатов без вывода в консоль.
Можно ли оптимизировать вычисления больших матриц и как это сделать?
Для работы с большими матрицами лучше использовать встроенные оптимизированные функции, такие как LinearSolve, Dot для умножения, Eigenvalues для собственных значений. Важно избегать избыточных циклов и по возможности использовать векторизованные операции. Кроме того, можно включить многопоточность в настройках и следить за эффективным управлением памятью.
Как сохранить созданный в Mathematica график в виде изображения с высоким разрешением?
Чтобы сохранить график в файл, применяют Export с указанием формата, например PNG или PDF. Для высокого разрешения при экспорте можно использовать опцию ImageResolution. Пример: Export[«график.png», график, ImageResolution -> 300]. Это позволит получить изображение с детализацией, подходящей для печати или публикации.
Как в Wolfram Mathematica построить график функции с несколькими параметрами?
Для построения графика функции с параметрами в Wolfram Mathematica можно использовать функцию Plot, задавая параметры как переменные с фиксированными значениями. Например, если у вас есть функция f[x_, a_] := a x^2, вы можете построить график при разных значениях параметра a, вызвав Plot[f[x, 1], {x, -5, 5}] для a=1. Чтобы визуализировать несколько кривых на одном графике, примените Plot[{f[x, 1], f[x, 2], f[x, 3]}, {x, -5, 5}]. Это позволит сравнить поведение функции при различных параметрах.