Mathcad предоставляет инженерам и ученым возможность выполнять вычисления в привычной математической нотации. Одной из ключевых возможностей среды является ввод и редактирование функций – как встроенных, так и пользовательских. При работе с функциями важно учитывать синтаксис языка Mathcad, который отличается от традиционных языков программирования.
Для создания функции в Mathcad используется конструкция имя функции(аргументы) := выражение. Например, функция f(x) := x² + 2x — 5 определяет квадратичную зависимость. Все переменные чувствительны к регистру. Вызов функции осуществляется простым указанием имени и значений аргументов, например: f(3).
В Mathcad доступны все базовые математические функции: sin, cos, exp, ln, sqrt и др. Они автоматически обрабатываются системой без необходимости подключения библиотек. Кроме того, возможно определение функций с несколькими аргументами и использование условных выражений с помощью оператора if. Например, g(x) := if x > 0, then x², else -x.
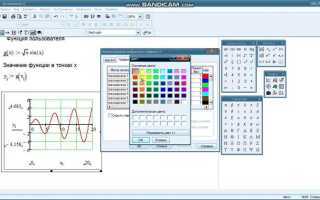
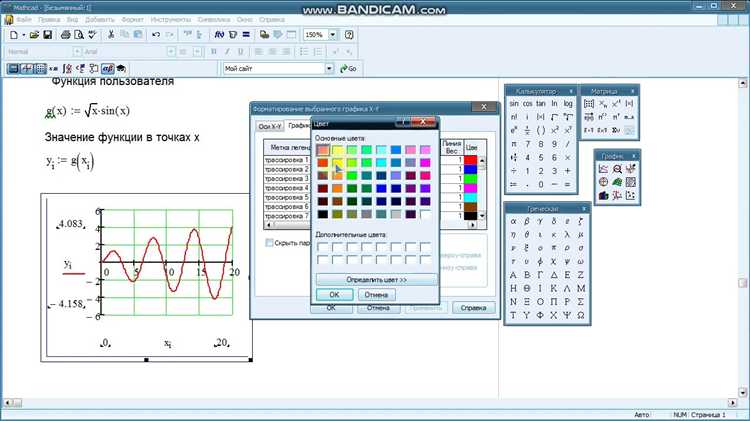
Mathcad позволяет визуализировать поведение функции с помощью встроенных графиков. После определения функции достаточно использовать компонент «X-Y Plot», задать диапазон значений и отобразить зависимость. Это существенно упрощает анализ поведения функций при различных параметрах.
Как записывать стандартные математические функции в рабочем окне Mathcad

Для ввода стандартных математических функций в Mathcad используется естественный синтаксис, максимально приближенный к привычной математической записи. Все функции вводятся в рабочем окне прямо в виде выражений, без необходимости использования меню или командной строки.
Функции вводятся на английском языке. Например, синус – sin(x), логарифм – ln(x) или log(x) (натуральный и десятичный соответственно), экспонента – exp(x). Скобки обязательны даже при наличии одного аргумента.
При вводе функций Mathcad автоматически интерпретирует их как встроенные. Например, при вводе cos(π) результат моментально подставляется в числовом виде. Переменные в аргументах должны быть определены ранее или задаются символически.
Для возведения в степень используется оператор ^. Запись x^2 моментально преобразуется в отображение степенного выражения. Квадратный корень – sqrt(x). Отдельная функция для корня n-й степени – nthroot(x, n).
Тригонометрические функции: sin(x), cos(x), tan(x) работают в радианах. Если необходимы градусы, следует умножить аргумент на deg или использовать преобразование единиц.
Гиперболические функции: sinh(x), cosh(x), tanh(x) вводятся аналогично. Обратные функции записываются как arcsin(x), arccos(x), arctan(x).
Для вычисления значений функций необходимо задать выражение с использованием знака равенства =. Например, f(x) := sin(x) + x^2 – определение функции, а f(2) = – вызов с вычислением результата.
Mathcad различает регистр символов. Функция Log(x) интерпретируется как пользовательская, если не задана, в отличие от встроенной log(x).
Автозавершение помогает при вводе: начните печатать имя функции, и система предложит варианты. Это ускоряет ввод и снижает количество ошибок.
Использование встроенных функций для работы с тригонометрией и логарифмами

Mathcad поддерживает прямое введение тригонометрических и логарифмических функций с автоматическим распознаванием синтаксиса. Для тригонометрии доступны функции sin(x), cos(x), tan(x), cot(x), а также их обратные: arcsin(x), arccos(x), arctan(x), arccot(x). Углы по умолчанию интерпретируются в радианах. Чтобы использовать градусы, необходимо указать единицу deg: sin(30 * deg).
При работе с логарифмами Mathcad различает десятичный и натуральный логарифмы. Натуральный логарифм вводится как ln(x), десятичный – log(x). Для логарифмов по произвольному основанию используется конструкция log(x, a), где a – основание. Например, log(8, 2) возвращает 3.
Важно помнить: Mathcad автоматически упрощает выражения. Например, ln(exp(x)) возвращает x, а sin(arcsin(x)) упрощается до x, если x лежит в допустимом диапазоне. При вводе сложных выражений рекомендуется использовать круглые скобки для явного указания порядка операций.
Встроенные функции поддерживают векторные и матричные аргументы. Пример: sin([0, π/2, π]) возвращает массив значений [0, 1, 0]. Это позволяет легко применять функции к целым наборам данных без явных циклов.
Для точных вычислений с логарифмами и тригонометрией отключите автоматическое округление в настройках отображения и убедитесь, что аргументы выражены в совместимых единицах измерения. Mathcad чувствителен к единицам, и несоответствие может привести к ошибкам или некорректным результатам.
Ввод пользовательских функций с параметрами и их вызов
Для создания пользовательской функции в Mathcad используйте конструкцию определения: после имени функции указываются параметры в круглых скобках, а затем – двоеточие и выражение, определяющее поведение функции.
Пример:
f(x, y) := x² + y²
Данная функция принимает два аргумента и возвращает сумму их квадратов. После определения функция становится доступной для вызова с конкретными значениями параметров:
f(3, 4) вернёт 25.
Внутри пользовательской функции можно использовать встроенные математические операторы, условные выражения и даже другие ранее определённые функции.
Использование условных операторов:
g(x) := if x < 0 then -1 else if x = 0 then 0 else 1
Функция g(x) реализует знак числа. Для отрицательного x вернёт -1, для нуля – 0, для положительного – 1.
Функции могут принимать в качестве параметров векторы и матрицы. Для корректной работы необходимо учитывать размерности и операции, совместимые с этими типами данных.
Пример с вектором:
sumVec(v) := sum(v)
Вызов sumVec(<1, 2, 3>) даст результат 6.
Определённые функции чувствительны к области определения. Убедитесь, что при вызове не происходит деления на ноль, логарифмирования отрицательных чисел и других некорректных операций. Mathcad не выполнит вызов и сообщит об ошибке при нарушении математических ограничений.
Функции можно размещать в любом месте рабочего листа, но вызов возможен только после их определения. Рекомендуется размещать определения выше по листу или использовать блоки для логической структуры документа.
Ошибки при вводе функций: как распознать и исправить
Mathcad строго различает математические выражения по типу ввода. Малейшее отклонение от синтаксиса приводит к некорректному результату или полной недееспособности выражения. Ниже перечислены ключевые ошибки и способы их устранения.
- Неправильное использование оператора присваивания: Символ := используется для задания функции или переменной, тогда как = служит для вычислений. Пример: f(x) := x^2 корректно, f(x) = x^2 – вызовет ошибку.
- Пропуск аргументов функции: При определении функций необходимо указывать все переменные. Ошибка возникает при вводе g := x + y без определения зависимостей от x и y, вместо g(x, y) := x + y.
- Использование скобок: Mathcad различает круглые скобки (функции), квадратные (индексы), фигурные (матрицы). Ошибка: f[x] вместо f(x).
- Конфликт имен: Переменная с тем же именем, что и встроенная функция (например, log), приведет к переопределению. Рекомендуется избегать таких совпадений или использовать индексные обозначения.
- Неправильный порядок операций: Mathcad выполняет вычисления по собственным приоритетам. Пример ошибки: 1/2x интерпретируется как (1/2) * x, но 1/(2x) требует явного использования скобок: 1/(2*x).
- Использование неинициализированных переменных: При вводе функции, использующей переменную без предварительного определения, результатом будет ошибка или неопределенность.
- Отсутствие единиц измерения: Если в расчетах участвуют физические величины, Mathcad требует явного указания единиц. Пример: v := 10 – недостаточно, необходимо v := 10 m/s.
Для быстрого выявления ошибок используйте встроенную проверку синтаксиса и подсветку. Любое выражение, подсвеченное красным, указывает на синтаксическую ошибку. Наведение курсора покажет краткое описание проблемы. Для отладки сложных функций рекомендуется поэтапный ввод с промежуточной проверкой каждого выражения.
Работа с функциями нескольких переменных и отображение их графиков
В Mathcad для задания функции нескольких переменных необходимо использовать определение функции с явным перечислением всех переменных. Например, функция f(x, y) := x² + y² задаётся с помощью символа определения :=. Обе переменные должны быть объявлены либо иметь числовые диапазоны.
Для построения графика функции двух переменных используется компонент «поверхность» (3D Plot). Перед созданием графика необходимо задать диапазоны переменных с помощью оператора диапазона. Например: x := 0, 0.1..10, y := 0, 0.1..10. Это позволит функции построиться по сетке значений переменных.
График вызывается через вкладку «Вставка» → «График» → «График поверхности». В поле для функции вводится выражение, использующее ранее определённую функцию. При необходимости можно задать масштаб вручную: щелчком по осям и вводом желаемых значений диапазонов X, Y и Z.
При работе с функциями, имеющими особенности (асимптоты, разрывы), следует использовать условные конструкции внутри функции: например, оператор if или piecewise. Это позволит избежать ошибок построения и некорректного отображения.
Для более точного контроля графика рекомендуется уменьшить шаг в диапазонах переменных, но это увеличивает нагрузку на систему. Оптимальным считается шаг 0.1 для большинства инженерных задач. При сложной поверхности имеет смысл использовать сглаживание через функцию spline по заранее рассчитанным точкам.
Импорт и использование внешних функций в формате DLL и других языках
Mathcad поддерживает интеграцию внешних функций через динамические библиотеки DLL, что расширяет возможности расчетов за счет использования кода, написанного на C, C++, Fortran и других языках. Для подключения DLL необходимо воспользоваться функцией ImportDLL, указав путь к библиотеке и прототип функции с точным описанием типов входных и выходных параметров.
При создании DLL важно учитывать соглашение о вызове функций (например, __stdcall или __cdecl), так как неправильный выбор приводит к ошибкам выполнения. Для Mathcad предпочтительно использовать __stdcall, обеспечивающее корректную работу с параметрами и стеком.
Функции из DLL должны иметь экспортируемые имена, которые не подвергаются манглингу; в C++ рекомендуется использовать extern «C» для отключения искажения имен. Если DLL содержит несколько функций, Mathcad позволяет подключать их выборочно, повторяя команду импорта с разными именами.
Для вызова функций из других языков, таких как Python или MATLAB, Mathcad предоставляет интерфейсы через COM-объекты или ActiveX. Настройка требует регистрации соответствующих библиотек и указания путей к исполняемым файлам. Использование COM-компонентов позволяет передавать сложные структуры данных и управлять выполнением скриптов внутри Mathcad.
При работе с внешними функциями необходимо тщательно проверять корректность типов и количество параметров, поскольку Mathcad не обеспечивает автоматическую проверку соответствия сигнатур. Для отладки рекомендуется создавать простые тестовые функции и последовательно увеличивать сложность.
Рекомендуется документировать все параметры и возвращаемые значения, указывая единицы измерения и ожидаемый формат данных, чтобы избежать ошибок при интеграции. Также следует учитывать особенности платформы (32- или 64-битная версия Mathcad), так как DLL должны соответствовать архитектуре программы.
Вопрос-ответ:
Как в Mathcad правильно вводить математические функции с параметрами?
Для ввода функции с параметрами в Mathcad необходимо использовать синтаксис, при котором сначала задаётся имя функции, затем в скобках перечисляются переменные. Например, для функции f(x, y) нужно написать: f(x, y) := выражение. При этом двоеточие и знак равенства := служат для определения функции, а переменные можно использовать внутри выражения, задавая необходимую формулу.
Можно ли в Mathcad задавать функции с несколькими аргументами и использовать их для вычислений?
Да, Mathcad поддерживает функции с несколькими аргументами. Для этого в определении функции нужно указать все необходимые переменные через запятую. Например, функция g(a, b, c) := a^2 + b*c принимает три входных параметра и возвращает результат по формуле. После определения функции можно подставлять конкретные значения аргументов, например, g(2, 3, 4), и получить численное значение.
Как вводить в Mathcad функции, содержащие условные выражения или ветвления?
Для реализации условий внутри функций в Mathcad используют оператор if. Например, функция, которая возвращает одно значение, если условие истинно, и другое — если ложно, записывается так: h(x) := if x > 0 then x^2 else -x. Здесь сначала задаётся проверка условия, затем через ключевые слова then и else определяются различные варианты результата. Такой подход позволяет создавать более сложные функции с логикой выбора.
Как в Mathcad обращаться к встроенным математическим функциям при вводе своих выражений?
В Mathcad имеется обширный набор стандартных функций, таких как синус, косинус, экспонента, логарифмы и др. Чтобы использовать их, достаточно ввести имя функции и аргумент в скобках, например, sin(x) или ln(y). При составлении собственных функций можно свободно комбинировать эти встроенные вызовы с арифметическими операциями и переменными, создавая нужные формулы.
Можно ли в Mathcad создавать функции, которые возвращают вектор или матрицу?
Да, Mathcad позволяет создавать функции, результатом которых является вектор или матрица. Для этого внутри функции используют конструкции, формирующие массивы, например, с помощью скобок [] или функции для создания матриц. Например, функция vec(t) := [t, t^2, t^3] создаёт вектор из трёх элементов, зависящих от параметра t. Аналогично можно строить матрицы, задавая элементы по строкам и столбцам.
Как вводить математические функции в Mathcad: с чего начать?
Для ввода математической функции в Mathcad достаточно выбрать область для записи формулы и воспользоваться встроенной панелью инструментов. Например, для создания функции f(x) = x^2 + 3x — 5 нужно ввести имя функции с аргументом, затем знак равенства и после этого формулу. Mathcad автоматически распознает переменные и операторы, а также позволит сразу увидеть результат при подстановке значений.