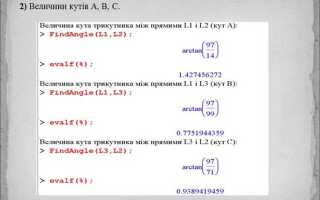
Как взять производную в maple

В Maple вычисление производной начинается с определения выражения. Используется функция diff, которая принимает два аргумента: само выражение и переменную дифференцирования. Например, для функции f(x) = x^3 + 2x вводится diff(x^3 + 2*x, x).

Чтобы сохранить результат и использовать его в дальнейших вычислениях, применяют оператор присваивания. Пример: df := diff(x^3 + 2*x, x). Это создаёт новую переменную df, содержащую первую производную функции.

Для нахождения производной высших порядков указывается дополнительный параметр. Например, diff(x^3 + 2*x, x$2) возвращает вторую производную. Символ $ означает повторение операции дифференцирования по той же переменной.

Maple позволяет брать частные производные. Если функция зависит от нескольких переменных, например f(x, y) = x^2 * y + sin(y), то производную по y получают командой diff(x^2*y + sin(y), y). Для смешанных производных используют вложенные вызовы: diff(diff(x^2*y + sin(y), x), y).

Для повышения читаемости кода рекомендуется использовать явное определение функции через f := (x) -> x^3 + 2*x, а затем производную записывать как D(f)(x). Это особенно удобно при работе с абстрактными функциями и операторной записью.

Как задать функцию для дифференцирования в Maple

Для задания функции в Maple используйте оператор присваивания `:=` и синтаксис, включающий стрелку `->`. Пример: f := x -> x^2 + sin(x); создаёт функцию f(x) = x² + sin(x). Это позволяет использовать функцию с переменной в качестве аргумента и применять к ней операторы дифференцирования.

Для многопеременных функций указывайте все переменные в круглых скобках: f := (x, y) -> x^2 + y^2;. В этом случае Maple корректно распознаёт все аргументы при последующем дифференцировании по одной из переменных.

Если необходимо задать выражение без использования функциональной стрелки, можно ввести его напрямую: expr := x^3 * ln(x);. В этом случае для взятия производной потребуется явно указать переменную: diff(expr, x);.

Избегайте путаницы между выражением и функцией. Выражение – это просто формула, функция – это правило отображения. Для автоматизированного дифференцирования предпочтительнее использовать функции через `->`, так как это позволяет легко изменять переменные и применять аналитические методы Maple.

Использование команды diff для взятия производной

Команда diff в Maple используется для аналитического взятия производных по заданной переменной. Синтаксис: diff(f(x), x), где f(x) – выражение, а x – переменная дифференцирования.

Для взятия производной второго и выше порядков используется третий аргумент: diff(f(x), x$n), где n – порядок производной. Например, diff(sin(x), x$3) возвращает третью производную от sin(x) по x.

При дифференцировании по нескольким переменным аргументы перечисляются через запятую: diff(f(x, y), x, y) – сначала по x, затем по y. Для производной второго порядка по одной переменной и первого по другой – diff(f(x, y), x$2, y).

Если переменная явно не указана, Maple не может корректно выполнить дифференцирование. Следует избегать выражений вроде diff(f) без аргументов.

Для сохранения результата в переменную используется оператор присваивания: df := diff(f(x), x);. Это позволяет использовать производную в дальнейших вычислениях без повторного вызова diff.

При работе с функциями, определёнными как f := x -> x^2 + 3*x, необходимо применять D(f) для получения производной: D(f)(x) вернёт 2*x + 3. Это ключевое отличие от diff, который работает только с выражениями, а не с функциональными объектами.

Вычисление производной по нескольким переменным

Для дифференцирования по нескольким переменным в Maple используется функция diff с указанием переменной и, при необходимости, порядка производной. Формат: diff(выражение, переменная) или diff(выражение, переменная$n), где n – порядок производной.

Пример: diff(x^2*y + sin(x*y), x) вернёт 2*x*y + y*cos(x*y). Производная берётся только по x, y считается константой.

Для смешанной производной указываются обе переменные: diff(x^2*y + sin(x*y), x, y). Результат: 2*x + cos(x*y) - x*y*sin(x*y). Maple последовательно применяет частные производные по каждой переменной.

Чтобы вычислить частные производные по нескольким переменным второго порядка, например, ∂²f/∂x² и ∂²f/∂x∂y, используйте: diff(f, x$2) и diff(f, x, y).

Если требуется вычислить градиент, используйте команду Gradient из пакета VectorCalculus: with(VectorCalculus): Gradient(f(x,y,z), [x,y,z]). Это даст вектор частных производных по всем переменным.

Для получения гессиана применяйте Hessian: Hessian(f(x,y), [x, y]). Maple вернёт матрицу вторых производных, упорядоченную по переменным.

В уравнениях с параметрами обязательно указывайте переменные, по которым берётся производная, чтобы избежать ошибок. Например, diff(a*x^2 + b*y^2, x) корректно обработает a как параметр, а не переменную.

Получение производной заданного порядка

Для вычисления производной n-го порядка в Maple используется функция diff с указанием порядка после переменной. Например, чтобы получить третью производную функции f(x) по переменной x, введите:

diff(f(x), x$3);

Символ $ позволяет задать порядок без необходимости повторять переменную. Выражение x$3 эквивалентно x, x, x.

Если требуется производная по нескольким переменным, можно комбинировать аргументы. Пример: пятая производная функции f(x, y), трижды по x и дважды по y:

diff(f(x, y), x$3, y$2);

Для анализа результата используйте команду simplify в связке с diff, чтобы сократить выражение:

simplify(diff(f(x), x$4));

Если функция задана явно, например f := x -> sin(x^2);, то:

diff(f(x), x$2);

вернёт вторую производную от sin(x²). Для символьных выражений, не определённых как функции, порядок указывается аналогично:

diff(sin(x^2), x$2);

При необходимости программного получения производных в цикле используйте seq:

seq(diff(f(x), x$i), i = 1..5);

Это создаст список производных от первого до пятого порядка.

Сохранение результата производной в переменную

В Maple результат взятия производной можно напрямую сохранить в переменную для последующего использования в вычислениях или построении графиков. Это делается с помощью оператора присваивания :=.

Пример: пусть необходимо сохранить производную функции f := x -> sin(x^2). Сначала вычисляем производную, затем сохраняем результат:

f := x -> sin(x^2):
df := D(f);

Теперь df – это функция, представляющая производную f. Можно использовать её как df(x) для вычисления значений производной.

Если требуется сохранить символическую производную выражения, а не функции, используйте:

expr := x^3*ln(x);
dexpr := diff(expr, x);

Переменная dexpr содержит аналитическое выражение производной. Оно пригодно для подстановок, упрощений, интегрирования и других операций.

Важно: не используйте знак = вместо :=, иначе Maple не выполнит присваивание. Также не путайте D(f) (для операторов функций) с diff(expr, x) (для обычных выражений).

Отображение производной в символьной и численной форме

В Maple производную можно получить и представить двумя основными способами: как символьное выражение и в виде численного значения. Правильное отображение обеих форм обеспечивает точность анализа и удобство последующей работы.

Символьное вычисление производной
- Используйте команду diff(функция, переменная) для получения точного аналитического выражения производной.
- Для удобства восприятия применяйте simplify() или expand() к результату, чтобы упростить или раскрыть скобки.
- Если требуется отображение в более привычной математической форме, используйте print()` или latex() для экспорта в LaTeX.


Численное вычисление производной

Для конкретного значения переменной используйте команду eval(diff(функция, переменная), переменная=число).
Пример: evalf(eval(diff(x^3, x), x=2)) выведет 12.0.
Если производная сложная, численные методы приближенного дифференцирования через NumericCalculus:-D дают значение с контролируемой точностью.


Рекомендации по отображению

Для повторного использования символьного выражения сохраните результат в переменную, избегая повторных вычислений.
При необходимости графического анализа можно построить график производной через plot(diff(...)), что визуально демонстрирует поведение функции.
Численное значение удобно использовать для проверки корректности символьных вычислений на выбранных точках.
Сочетание символьного и численного подходов облегчает оптимизацию и численные методы, где аналитическое выражение служит основой.


Вопрос-ответ:
Как в Maple получить производную функции с несколькими переменными?
Для нахождения частной производной функции с несколькими переменными в Maple используют команду diff, указывая функцию и переменную, по которой нужно дифференцировать. Например, если у вас есть функция f(x, y) := x^2 * y + sin(y), то частная производная по x будет вычисляться как diff(f(x, y), x), а по y — diff(f(x, y), y). Maple при этом автоматически вычисляет нужную частную производную.
Можно ли в Maple увидеть каждый шаг вычисления производной, а не только итоговый результат?
В стандартных настройках Maple сразу выдает результат производной без подробных промежуточных вычислений. Однако, чтобы проследить процесс пошагово, можно использовать команды simplify или expand между шагами, либо разложить вычисление на отдельные этапы вручную, поочередно применяя diff к частям выражения. Также есть учебные пакеты и специальные библиотеки, которые помогают демонстрировать каждый шаг, но они требуют дополнительной настройки.
Какие ограничения существуют при взятии производной сложных функций в Maple?
Maple справляется с большинством аналитических выражений, включая сложные тригонометрические, показательные и логарифмические функции. Тем не менее, если функция содержит неопределённые параметры или очень громоздкие составные выражения, вычисления могут занять много времени или не уместиться в стандартных ресурсах. В таких случаях можно использовать численные методы или упрощать функцию перед дифференцированием.
Как в Maple задать точку, в которой нужно вычислить значение производной?
После того как вы нашли производную функции, например diff(f(x), x), для вычисления её значения в конкретной точке x = a используйте подстановку: substitute(diff(f(x), x), x = a) или более компактно f'(a), если функция определена как f. Это позволяет быстро получить численное или символическое значение производной в нужной точке.
Можно ли в Maple автоматически вычислить производную высшего порядка и как это сделать?
Да, Maple позволяет находить производные любого порядка с помощью команды diff, где в качестве третьего аргумента указывается порядок производной. Например, diff(f(x), x$3) вычислит третью производную функции f по переменной x. Это упрощает работу, если нужно быстро получить производные второго, третьего или более высокого порядка без повторного применения команды.
Как в Maple можно вычислить производную функции с несколькими переменными шаг за шагом?
Для вычисления производной функции нескольких переменных в Maple поэтапно можно использовать команду `diff` с указанием переменной, по которой берется производная. Чтобы увидеть промежуточные шаги, полезно применять пакеты для пошагового решения, например, `Student[Calculus1]`. Там есть функция `StepwiseDerivative`, которая выводит процесс дифференцирования по каждой переменной отдельно, объясняя, какие правила применяются. Таким образом, можно получить подробное представление о вычислении частных производных, даже для сложных выражений.
Можно ли в Maple настроить вывод производной так, чтобы сразу показывались упрощения и сокращения выражения?
Да, в Maple есть возможность автоматически упрощать результат вычисления производной. Для этого после применения функции `diff` можно использовать команды из пакета `simplify`, например, `simplify` или `expand`, чтобы преобразовать выражение к более компактному виду. Также существуют опции внутри пакета для настройки уровня упрощения и преобразований, что помогает получать конечный результат, более удобный для анализа. Это позволяет видеть не только саму производную, но и ее оптимизированный вид без лишних сложных частей.