В среде Mathcad вычисление производных выполняется с помощью встроенной функции derivative и символического оператора ‘. Эти инструменты позволяют дифференцировать как простые алгебраические выражения, так и сложные функции с параметрами. Например, для функции f(x) := x^2 + sin(x) запись f'(x) автоматически даст аналитическую производную 2x + cos(x).
Чтобы задать производную по конкретной переменной, важно правильно структурировать выражение. Mathcad различает численное и символическое дифференцирование: символическое выполняется через клавишу [Ctrl] + [.] после выбора выражения, а численное требует задания точек и значений переменных. Важно учитывать, что производные в Mathcad чувствительны к единицам измерения, и ошибки часто возникают из-за несогласованных размерностей.
Для дифференцирования составных функций рекомендуется использовать вложенные определения. Например, при задании g(t) := f(sin(t)), выражение g'(t) корректно применит правило производной сложной функции. Для многомерных функций, таких как f(x, y), частные производные записываются в форме ∂f/∂x, что достигается комбинацией символического оператора и функции partial derivative.
В случае необходимости автоматизации вычислений на множестве точек удобно использовать векторы. Задав x := 0, 0.1 .. 10 и f(x) := ln(x), можно получить численную производную в виде вектора, используя функцию diff. При этом важно следить за корректным определением границ области, чтобы избежать логарифмов от отрицательных значений.
Как ввести переменную и функцию для дифференцирования
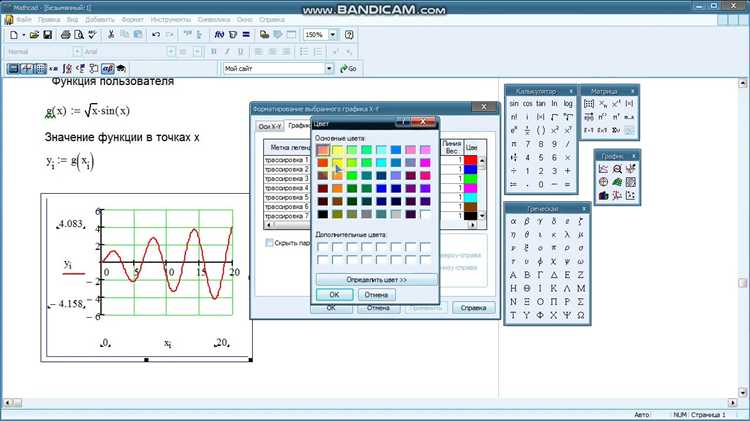
Для задания переменной в Mathcad используйте символ присваивания двоеточие :=. Например, чтобы определить переменную x, просто введите x := и значение при необходимости.
Чтобы задать функцию, укажите имя функции, круглые скобки с переменной и знак присваивания. Пример: f(x) := x^2 + sin(x). Mathcad автоматически распознает x как независимую переменную.
Перед дифференцированием убедитесь, что функция определена корректно. Проверить это можно, вызвав функцию с конкретным аргументом, например: f(2). Если результат отображается численно, выражение задано правильно.
Дифференцируемая переменная не требует отдельного объявления типа. Однако, если используется несколько переменных, например x и y, следует чётко указывать, по какой переменной производится дифференцирование.
Избегайте использования одинаковых имен для переменных и функций – это вызывает конфликт имён и ошибки вычислений.
Синтаксис оператора производной в Mathcad

В Mathcad для обозначения производной используется апостроф ('). Запись f'(x) означает первую производную функции f по переменной x. Для получения второй производной используется двойной апостроф: f''(x). Точно так же обозначаются производные более высоких порядков: f'''(x), f''''(x) и так далее.
Производную можно вычислить и в точке. Для этого указывается выражение вида f'(x) =, после чего подставляется значение переменной x := число. Mathcad автоматически подставит значение и вычислит результат.
Если необходимо вычислить частную производную, используется встроенная функция ∂/∂x, доступная через панель символов или сочетание клавиш. Например, запись ∂f(x, y)/∂x означает частную производную функции f по переменной x.
Важно: Mathcad различает символьное и численное дифференцирование. Для символьного результата используется команда symbolic или нажимается [Ctrl]+. после выражения. Без этого производная будет рассчитана численно при наличии конкретных значений переменных.
Также допускается задание функции через определение, например f(x) := x^3 + 2·x, после чего можно напрямую обращаться к f'(x) или f''(x) без повторного ввода выражения.
Использование символического вычисления для получения аналитической производной
Для получения аналитической производной в Mathcad необходимо использовать оператор символического вычисления. Он обозначается знаком «=>», который размещается после выражения, подлежащего дифференцированию.
Чтобы найти производную функции f(x), сначала введите её явно, например: f(x) := sin(x^2) + ln(x). Затем укажите выражение для производной: d/dx f(x). После этого нажмите клавишу [Ctrl + .], чтобы вставить символ «=>» справа от выражения. Mathcad выполнит символическое дифференцирование и отобразит результат в аналитической форме.
Для получения производной более высокого порядка укажите степень производной в числителе: d^2/dx^2 f(x) – вторая производная. В Mathcad допустимы частные производные: d/dx f(x, y) возвращает производную по x, независимо от y.
Если необходимо упростить полученное выражение, добавьте команду simplify после «=>»: d/dx f(x) => simplify. Это особенно полезно для сложных выражений, где результат может быть представлен в более компактной форме.
Операция дифференцирования может применяться и к выражениям напрямую, без предварительного присваивания: d/dx (e^(x^2) * tan(x)) =>. Mathcad рассчитает производную сразу, без необходимости задания функции.
Для контроля результатов рекомендуется использовать функцию check с подстановкой значений: сравните численное значение аналитической производной с численной производной с помощью функции derivative(f(x), x) при фиксированном x.
Численное дифференцирование в точке
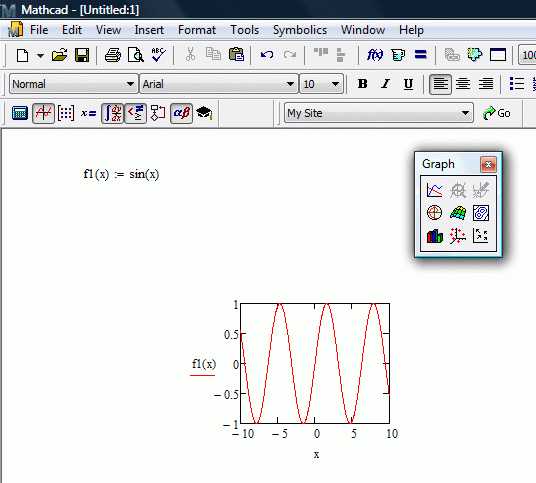
f′(x₀) ≈ (f(x₀ + h) − f(x₀ − h)) / (2h)
Погрешность данного метода составляет O(h²), что делает его предпочтительным по сравнению с односторонними схемами. В Mathcad необходимо заранее задать шаг h, например:
h := 0.001
Затем определить функцию f(x), например:
f(x) := sin(x)
И записать выражение для производной:
df := (f(x + h) − f(x − h)) / (2·h)
Для вычисления в конкретной точке x₀, например, x := π/4, просто подставьте значение x:
df
Mathcad автоматически выполнит подстановку и рассчитает приближённое значение производной. При выборе h следует избегать слишком малых значений из-за машинной точности, оптимальный диапазон: от 10⁻³ до 10⁻⁵.
Если функция представлена набором дискретных точек, используйте встроенную функцию deriv с индексом нужной точки:
deriv(v, i, h)
Где v – вектор значений, i – индекс точки, h – шаг между элементами. Убедитесь, что i не находится на границе массива, иначе метод не применим.
Дифференцирование составных и вложенных функций
В Mathcad для нахождения производной составной или вложенной функции применяется цепное правило. Это особенно важно при работе с функциями вида \( f(g(x)) \), где внешняя и внутренняя функции имеют разную структуру.
- Для задания функции используйте определение через знак присваивания (:=), например:
g(x) := x^2 + 1,f(u) := sin(u). - Составную функцию определяют как:
h(x) := f(g(x)). - Для нахождения производной используйте оператор производной:
h'(x)или∂/∂x h(x).
Mathcad автоматически применяет правило цепочки. В примере выше результат будет равен cos(g(x)) * g'(x), что в точной записи даст: cos(x^2 + 1) * 2x.
Если необходимо задать более сложную вложенность, используйте вложенные определения:
u(x) := ln(x^2 + 3)v(x) := exp(u(x))v'(x)выдаст результат:exp(ln(x^2 + 3)) * (2x / (x^2 + 3))
При численном дифференцировании указывайте конкретное значение переменной: v'(2). Mathcad выполнит подстановку и вычисление без необходимости ручного дифференцирования.
Избегайте смешивания переменных. Все внутренние функции должны быть определены в терминах тех же переменных, что и внешняя, иначе Mathcad вернёт ошибку несовместимости.
Как задать производную по нескольким переменным
В Mathcad частные производные вводятся с помощью оператора дифференцирования. Чтобы задать производную функции f(x, y) по переменной x, используйте запись: ∂/∂x f(x, y). Символ частной производной вызывается через панель «Calculus» или комбинацией клавиш Ctrl + Shift + D, после чего указывается переменная дифференцирования.
Для вычисления производной по нескольким переменным последовательно применяйте оператор частной производной. Например, чтобы найти ∂²f/∂x∂y, сначала введите ∂/∂y, затем примените его к выражению ∂/∂x f(x, y). Mathcad поддерживает вложенные производные, и порядок указания переменных имеет значение при вычислении непеременных смешанных производных.
Если требуется аналитическое выражение, убедитесь, что функция определена символьно. Например, f(x, y) := x²·sin(y). После ввода производной нажмите = – результат будет выражен в символьной форме. Для численного расчёта используйте функцию numderiv(f, x, y) с подстановкой конкретных значений переменных.
Mathcad автоматически упрощает выражения, но при необходимости используйте команду simplify для ручного управления преобразованием. Чтобы сохранить структуру вычислений, рекомендуется назначать промежуточные производные переменным, например: dfdx := ∂/∂x f(x, y).
Обозначение и использование производной второго и более высокого порядка

В Mathcad для обозначения производных второго и более высокого порядка применяется функция производной с указанием порядка. Для второй производной синтаксис выглядит так:
derivative(f(x), x, 2)
где f(x) – функция, x – переменная, по которой берётся производная, 2 – порядок производной.
Для производных третьего, четвёртого и выше порядка достаточно менять число в третьем аргументе функции derivative.
- Третья производная:
derivative(f(x), x, 3) - Четвёртая производная:
derivative(f(x), x, 4) - И так далее
Mathcad автоматически вычисляет производные нужного порядка, если функция задана аналитически.
Рекомендуется для удобства предварительно определить функцию с помощью оператора присваивания, например:
f(x) := x^4 + 3*x^2 - 7
После этого вычисление второй производной будет выглядеть так:
derivative(f(x), x, 2)
При численном задании функции через массивы или табличные значения производные более высокого порядка вычислять сложнее и требует использования специальных методов аппроксимации.
В качестве альтернативы можно использовать оператор дифференцирования ' в Mathcad Prime, например:
f''(x)
означает вторую производную функции f(x). Для третьей и выше производных количество апострофов увеличивается соответственно (f'''(x), f''''(x)).
Использование оператора апострофа удобно для компактного и наглядного представления производных в формулах.
- Определите функцию явно или через выражение.
- Для производных порядка выше первого используйте функцию
derivativeс третьим аргументом или оператор'. - Проверяйте результаты на простых тестовых функциях для уверенности в правильности записи.
Частые ошибки при записи производной и способы их исправления
Одна из типичных ошибок – попытка использовать обычный оператор деления для обозначения производной, например, f'(x) = (f(x + h) — f(x)) / h без правильного контекста. В Mathcad нужно применять встроенную функцию производной, обозначаемую символом d/dx, или использовать оператор prime (штрих). Ручной ввод дроби часто приводит к неверному результату.
Еще одна ошибка – неправильный выбор переменной дифференцирования. В выражении производной обязательно должна совпадать переменная, относительно которой вычисляется производная, с той, что используется в функции. Например, для f(x,y) производная по x записывается как d/dx f(x,y), а не просто d/dy или без указания переменной.
Некорректное применение производной к сложным выражениям без раскрытия скобок часто ведет к синтаксическим ошибкам. В Mathcad рекомендуется использовать функцию expand() перед вычислением производной, чтобы избежать проблем с вложенными функциями и операторами.
Ошибка в порядке операций при записи производной встречается, когда знак производной ставится к выражению с несколькими слагаемыми без уточнения области действия. В Mathcad нужно явно группировать выражение в скобках: d/dx (u + v) вместо d/dx u + v, иначе будет вычислена производная только для первого слагаемого.
Неверное использование обозначения d(x)/dx вместо d/dx x – это синтаксическая ошибка, так как d() – это не функция, а оператор дифференцирования. В Mathcad дифференцирование пишется как d/dx x, либо prime(x). Исправление состоит в корректном применении встроенных операторов.
При численном дифференцировании часто забывают задавать малое значение шага h. Mathcad автоматизирует этот процесс, но при ручном подходе нужно задавать h достаточно малым (например, 10⁻⁶) и использовать limit для точности, иначе результат будет неточным.
Для проверки правильности записи производной используйте встроенную функцию simplify() и сравнивайте полученный результат с аналитическим значением. Это позволит быстро выявить ошибки в записи и вычислениях.
Вопрос-ответ:
Как в Mathcad записать производную функции вручную, без использования готовых кнопок?
Для записи производной вручную в Mathcad нужно ввести выражение функции, затем поставить знак апострофа (‘) после переменной или функции. Например, для функции f(x) = x^2, производная будет записана как f'(x). Это создаст обозначение производной первого порядка. Важно, чтобы функция была определена в рабочей области перед этим.
Какие типы производных можно вычислить в Mathcad и как это отразить в записи?
В Mathcad можно записывать производные первого, второго и более высоких порядков, а также частные производные для функций нескольких переменных. Для производной второго порядка используют двойной апостроф, например, f»(x). Для частных производных вводят знак ∂ — его можно найти в панели символов, или использовать соответствующую функцию diff. При работе с несколькими переменными записывают, например, ∂f/∂x или diff(f,x).
Почему при вводе производной в Mathcad появляется ошибка, и как её избежать?
Частая причина ошибки — отсутствие определения функции до записи производной. Mathcad требует, чтобы функция была задана явно с помощью оператора присваивания, например, f(x) := x^2 + 3. Если попытаться сразу ввести f'(x) без определения f, программа не распознает символ. Кроме того, стоит проверять, что используется правильный синтаксис — апостроф ставится именно после имени функции, а не переменной.
Можно ли в Mathcad записать производную по параметру, если функция зависит от нескольких переменных? Как это сделать?
Да, для записи производной по одному из параметров при наличии нескольких переменных в Mathcad используют частные производные. Записывают функцию, например, z(x,y) := x^2 + y^3, затем вводят частную производную по x так: ∂z/∂x или diff(z,x). Ввод символа ∂ возможен через панель специальных символов или по коду, а функция diff позволяет гибко задавать порядок дифференцирования и переменную.