Как вычислить производную в mathcad

Mathcad предоставляет точные инструменты для аналитического и численного дифференцирования функций. Важно понимать, как правильно задать выражение, чтобы избежать ошибок в расчетах и получить корректный результат.

Для начала требуется определить функцию в виде переменной с использованием встроенного синтаксиса Mathcad. При этом необходимо следить за правильным указанием переменных и их областей определения. Это обеспечит корректность дальнейших операций.

Вычисление производной выполняется с помощью оператора d() или оператора аппроксимации diff() в случае численного дифференцирования. Правильное применение этих функций требует точного указания аргументов и порядка производной.

В этом руководстве приведены конкретные примеры с подробным описанием каждого шага, включая настройку вычислительных параметров и проверку результатов, что гарантирует точность и прозрачность расчетов.

Подготовка функции для дифференцирования в Mathcad

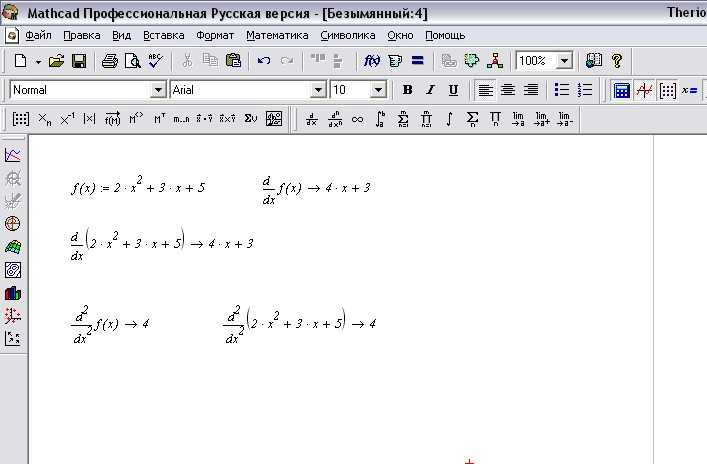
Перед вычислением производной необходимо правильно задать функцию. В Mathcad функция задаётся через знак равенства, например, f(x) := выражение. Для корректной работы дифференцирования важно соблюдать точное использование двоеточия и знака равенства, чтобы отличать определение функции от её вычисления.

Все переменные и параметры должны быть определены заранее. Если функция содержит параметры, им присваиваются значения перед определением функции или в самом выражении. Для многозначных функций или функций нескольких переменных используйте соответствующую нотацию, например, f(x, y) := …. При этом дифференцирование будет выполняться по указанной переменной.

Следует избегать использования неопределённых переменных и сложных вложенных конструкций в одном выражении функции, чтобы избежать ошибок при вычислении производной. В случаях сложных выражений рекомендуется разбивать функцию на промежуточные части, определяемые отдельно, с присвоением имен, что облегчает последующий анализ и отладку.

Mathcad чувствителен к синтаксису, поэтому функции с тригонометрическими, экспоненциальными и логарифмическими элементами должны быть записаны с использованием встроенных операторов, например, sin(x), exp(x), ln(x). Нельзя заменять их произвольными обозначениями.

Важный момент – проверка области определения функции. Если она ограничена, следует явно указать допустимые значения переменных, чтобы избежать некорректных результатов при вычислении производных.

После задания функции желательно визуально проверить её график, чтобы убедиться в корректности записи и отсутствии разрывов, что поможет избежать ошибок на следующих этапах дифференцирования.

Использование встроенной команды для вычисления производной

В Mathcad для вычисления производной применяется функция d(), которая реализует дифференцирование по заданной переменной. Синтаксис команды: d(f(x), x), где f(x) – выражение, от которого берется производная, а x – переменная дифференцирования.

Для вычисления производной функции в точке нужно сначала определить функцию, затем использовать команду с указанием переменной. Например, при задании f(x) := x^3 + 2*x производная по x вычисляется как d(f(x), x), результатом будет выражение 3*x^2 + 2.

Если требуется численное значение производной в конкретной точке, после вычисления символической производной следует подставить значение переменной, например: (d(f(x), x))|_{x=2}. В Mathcad это реализуется подстановкой x:=2 перед вычислением.

Для производных высших порядков используется повторное применение функции или встроенный второй параметр – порядок дифференцирования: d(f(x), x, 2) вычисляет вторую производную.

Обратите внимание, что функция d() корректно работает только с определённо заданными выражениями и переменными. В случаях с параметрическими или сложными функциями рекомендуется предварительно упростить выражение или явно определить переменные.

Определение точки вычисления производной

В Mathcad вычисление производной начинается с точного указания точки, в которой производная должна быть определена. Без этого шага результат будет некорректен или неполон.

Основные рекомендации по определению точки вычисления производной:

Точка задаётся числовым значением переменной, обозначающей аргумент функции (например, x = 2).
Если функция задана аналитически, используйте именно ту переменную, которая входит в выражение функции.
Для численного вычисления производной важно, чтобы значение точки лежало в области определения функции.
В случае параметрических или сложных функций следует проверить, что заданное значение не приводит к неопределённостям (например, деление на ноль).

В Mathcad для вычисления производной в конкретной точке используют синтаксис, где после оператора дифференцирования указывается переменная и точка вычисления:

Ввод функции, например: f(x) := x^3 + 2*x.
Определение точки: a := 1.5.
Вычисление производной в точке: df := derivative(f(x), x) | x=a или с использованием встроенной функции df := diff(f(x), x, a).

Обратите внимание, что в Mathcad ключевой момент – строгая привязка дифференцирования к переменной и конкретному значению, иначе результат будет представлен как общая формула, а не числовое значение.

Вычисление производной высших порядков в Mathcad

Для вычисления производных второго и последующих порядков в Mathcad применяется функция дифференцирования с параметром порядка. Основные шаги:

Определите функцию, для которой требуется найти производную. Пример: f(x):=x^3 + 2x^2 - x + 5.
Используйте оператор производной с указанием порядка: diff(f(x), x, n), где n – порядок производной (целое положительное число).
Например, для вычисления второй производной введите: diff(f(x), x, 2). Mathcad автоматически выполнит вычисление и отобразит результат.
Для третьей и более высоких производных аналогично указывайте нужный порядок: diff(f(x), x, 3) и так далее.

При работе с числовыми данными:

Если функция задана таблично, используйте численное дифференцирование через команду derivative, указав порядок и интервал.
Обратите внимание на выбор шага при численном дифференцировании: слишком большой шаг снижает точность, слишком малый может привести к числовым ошибкам.

Для упрощения повторных вычислений производных высших порядков рекомендуется:

Создать отдельные переменные для промежуточных производных первого порядка, что ускорит расчёты и улучшит читаемость.
Использовать встроенные функции Mathcad для символического вычисления, если задана аналитическая формула.

Таким образом, Mathcad позволяет быстро и корректно вычислять производные любого порядка при условии правильного задания функции и порядка дифференцирования.

Работа с производными сложных функций и выражений

Для вычисления производных сложных функций в Mathcad важно правильно задать выражение, учитывая синтаксис и порядок действий. При использовании вложенных функций следует применять скобки для точного определения границ дифференцируемого выражения.

Mathcad поддерживает автоматическое вычисление производных от функций, заданных через стандартные операции, а также от пользовательских функций. Для этого используется оператор дифференцирования, обозначаемый как d/dx или оператор prime (‘) для функций от одной переменной.

Если функция состоит из произведения, частного или сложной композиции, рекомендуется применять встроенные правила дифференцирования: правило произведения, частного и цепное правило. Например, для функции вида f(x) = g(x) * h(x) вычисление производной выполняется командой d/dx (g(x)*h(x)), и Mathcad автоматически применит соответствующее правило.

Для работы с функциями вида f(x) = sin(x²) или exp(3x + 1) необходимо явно задавать аргументы, чтобы Mathcad корректно применил цепное правило. Это достигается введением вложенных функций, например, sin(x^2) или exp(3*x + 1), и последующим дифференцированием по переменной x.

В случае функций нескольких переменных важно указывать переменную, по которой берется производная, с помощью оператора d/d(variable). Это особенно важно при вычислении частных производных сложных выражений с несколькими переменными.

Для упрощения вычислений и предотвращения ошибок рекомендуется разбивать сложные выражения на промежуточные функции и вычислять их производные по отдельности, после чего собирать итоговый результат.

Для контроля корректности вычислений стоит сравнивать результаты, полученные с помощью Mathcad, с аналитическими формулами или использовать графический анализ производной функции.

Применение численного дифференцирования в Mathcad

Численное дифференцирование в Mathcad используется для получения производных функций, заданных таблично или сложными выражениями, где аналитическое дифференцирование затруднено. Основной инструмент – оператор diff, который вычисляет приближенную производную по заданной переменной.

Для численного дифференцирования функции f(x) на конкретном значении x₀ применяется синтаксис diff(f(x), x, x₀). Mathcad автоматически выбирает шаг дифференцирования, но для повышения точности рекомендуется задавать шаг вручную с помощью выражения diff(f(x), x, x₀, h), где h – малое число, например, 10⁻⁵. Слишком большой шаг уменьшает точность, слишком маленький – увеличивает численные ошибки.

При работе с экспериментальными данными численное дифференцирование выполняется через функцию, построенную по массиву точек. В этом случае используется команда derivative вместе с интерполяцией, например, сплайнами, что обеспечивает сглаживание и уменьшение погрешностей.

Для ускорения вычислений и снижения ошибок рекомендуется минимизировать количество операций внутри дифференцируемой функции. Оптимально выносить константы и подвычислять фиксированные выражения вне оператора дифференцирования.

В Mathcad также реализованы методы центральных разностей, позволяющие повысить точность численного дифференцирования по сравнению с прямой аппроксимацией. Их использование доступно через расширенные опции функции diff или пользовательские шаблоны с формулами разностей.

Контроль точности достигается сравнением результатов численного дифференцирования при различных значениях шага h и анализом устойчивости результата. Для комплексных функций рекомендуется тестировать производную на известных аналитических примерах, чтобы проверить корректность настроек.

Проверка корректности вычисленной производной

После вычисления производной в Mathcad важно убедиться в правильности результата. Первый метод – аналитическая проверка: сравните полученное выражение с теоретической формулой производной исходной функции. Если функция простая, вычислите производную вручную и сопоставьте с результатом Mathcad.

Второй способ – численная проверка. Вычислите производную в нескольких точках с помощью Mathcad и приближенно оцените производную численным методом разностных частных, используя значения функции в соседних точках. Разница между этими значениями не должна превышать заданный уровень точности (например, 10^-6).

Mathcad позволяет использовать функцию «diff» для символического дифференцирования, однако при работе с сложными выражениями стоит проверить результат с помощью команды «eval» или построить графики функции и её производной. Если график производной демонстрирует логичное поведение (например, касательные касаются функции), результат вероятно корректен.

При использовании численных методов в Mathcad обратите внимание на параметры шага дифференцирования. Слишком большой шаг снижает точность, а слишком малый увеличивает вычислительную погрешность. Рекомендуется использовать шаг порядка 10^-4–10^-6.

Если вычисленная производная содержит неопределённые выражения или ошибки вычислений, Mathcad выведет предупреждения. В таких случаях проверьте правильность вводимых данных и корректность записи функции.

Сохранение и экспорт результатов производного анализа

Для сохранения вычисленных производных в Mathcad используйте команду File → Save As, выбрав формат .mcdx – нативный формат документа, сохраняющий все вычисления и графики без потерь. При работе с большими проектами рекомендуется разбивать вычисления на несколько файлов и сохранять промежуточные результаты, чтобы избежать потери данных.

Экспорт результатов в текстовый формат доступен через File → Export → Text. Этот способ полезен для интеграции с внешними системами или публикации расчетов. Экспортируются не только численные значения, но и выражения в виде текста, что облегчает последующую обработку.

Для передачи графиков и визуальных представлений производных воспользуйтесь функцией экспорта изображений: выделите график, затем File → Export → Image. Форматы PNG и SVG обеспечивают высокое качество при масштабировании, что важно для публикаций и презентаций.

Если требуется использовать данные в Excel, применяйте экспорт через Copy as → Table или прямой экспорт данных из массивов Mathcad в CSV. Это позволяет сохранить точность и структуру данных без преобразований.

Автоматизация сохранения возможна с помощью встроенного скрипта Mathcad Prime, где можно настроить регулярное сохранение и экспорт определенных переменных в указанные форматы, минимизируя риск потери данных при длительных расчетах.

Вопрос-ответ:

Как в Mathcad задать функцию для последующего вычисления её производной?

Для определения функции в Mathcad нужно ввести её выражение в рабочую область, например, y := x^2 + 3*x + 1. После этого можно применять инструменты вычисления производной. Важно правильно оформить функцию с использованием двоеточия и знака равенства :=, чтобы Mathcad воспринимал это именно как определение.

Какие способы вычисления производной доступны в Mathcad и как выбрать подходящий?

В Mathcad можно вычислять производные аналитически и численно. Аналитический способ подходит для выражений, заданных в явном виде, и выполняется с помощью встроенной функции производной (например, diff). Численный метод используют для сложных функций или данных, когда нужно получить приближённое значение. Выбор зависит от задачи: для точного выражения предпочтительнее аналитика, для табличных данных — численный подход.

Как выполнить вычисление производной по шагам с объяснением в Mathcad?

Чтобы показать процесс вычисления производной по шагам, можно последовательно вводить промежуточные вычисления: сначала задать функцию, затем записать правило дифференцирования, после этого вычислить производную каждого слагаемого и в конце сложить результаты. Mathcad позволяет вставлять текстовые комментарии рядом с вычислениями, что помогает объяснить каждый шаг. Это удобно для учебных целей и проверки правильности вычислений.

Можно ли в Mathcad вычислить производную сложной функции, содержащей тригонометрические и экспоненциальные выражения?

Да, Mathcad умеет работать с производными сложных функций, включая тригонометрические, логарифмические и экспоненциальные. Для этого достаточно корректно ввести формулу, используя стандартные обозначения sin(x), exp(x) и т.д. Затем командой diff можно получить выражение производной. Mathcad автоматически применит правила дифференцирования для каждого элемента, даже если функция составная и содержит несколько разных типов выражений.

Что делать, если Mathcad не вычисляет производную или выдаёт ошибку?

Если при попытке найти производную возникает ошибка, стоит проверить правильность записи функции: возможно, допущена синтаксическая ошибка или использованы неподдерживаемые символы. Также следует убедиться, что переменная для дифференцирования корректно определена и не конфликтует с другими элементами документа. В некоторых случаях помогает перезагрузка программы или повторный ввод выражения с соблюдением стандартных правил записи функций.

Как в Mathcad задать функцию для последующего вычисления её производной?

В Mathcad нужно сначала ввести функцию, используя переменную и оператор присваивания. Например, для функции f(x) = x^2 + 3x задайте в документе f(x) := x^2 + 3*x. Это позволит системе распознать выражение как функцию, с которой можно работать дальше, в том числе вычислять производные. Следующий шаг — использовать встроенную функцию для нахождения производной от f по переменной x.

Какие способы существуют для вычисления производной в Mathcad и в чем их отличие?

В Mathcad можно вычислять производные двумя основными методами. Первый — использовать символическое дифференцирование, которое доступно в версиях с поддержкой символьных вычислений. Для этого применяется оператор дифференцирования, который возвращает точный аналитический результат. Второй способ — численное приближение производной с помощью встроенных функций численного дифференцирования, если символьные возможности отсутствуют или необходим результат в конкретной точке. Символьный метод предпочтителен для получения формулы, численный — для быстрого расчёта конкретного значения.