Mathcad Prime – это мощный инструмент для решения математических задач, который включает в себя удобный интерфейс для записи и вычисления систем уравнений. Чтобы эффективно использовать его для записи, нужно понимать несколько ключевых аспектов: от правильного ввода уравнений до их оптимального отображения в рабочем листе. В этом руководстве мы рассмотрим процесс создания и решения системы уравнений в Mathcad Prime шаг за шагом.
Первым шагом при работе с системой уравнений в Mathcad Prime является использование оператора многоточия для разделения уравнений. Он позволяет записывать каждое уравнение в виде строки, обеспечивая четкую визуализацию. Система уравнений будет распознана программой, если все уравнения будут правильно оформлены и не содержать синтаксических ошибок.
Для записи системы в Mathcad Prime важно также учитывать приоритет операций. Программа автоматически выделяет операции по математическим законам, но при необходимости можно вручную корректировать приоритет с помощью круглых скобок. Важно помнить, что Mathcad Prime позволяет использовать как линейные, так и нелинейные уравнения, что расширяет возможности работы с системами разной сложности.
В процессе решения системы уравнений Mathcad Prime предлагает несколько методов, включая численные и аналитические методы. Для выбора метода решения можно использовать панель инструментов, где доступны различные опции для численного поиска корней или получения аналитических решений. Каждое решение будет отображено с точностью до выбранного вами числа знаков после запятой.
Таким образом, правильно настроив систему уравнений и выбрав соответствующий метод решения, вы сможете получить точные результаты и эффективно использовать Mathcad Prime для решения комплексных задач.
Запись системы уравнений в Mathcad Prime: пошаговая инструкция
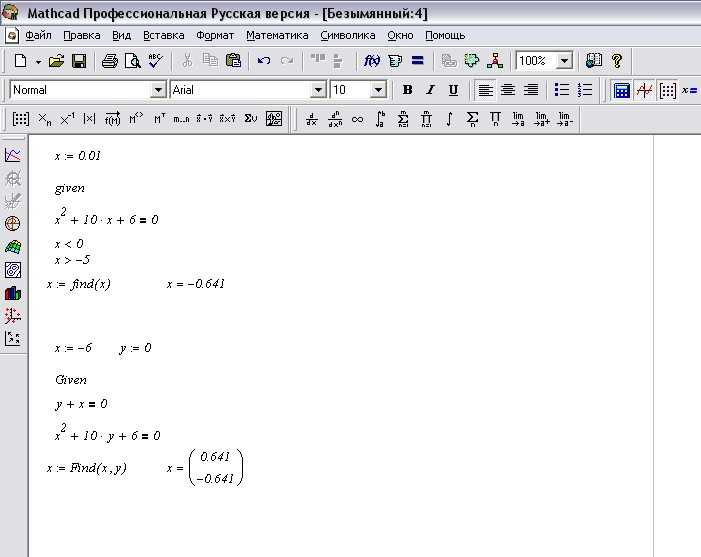
Для записи системы уравнений в Mathcad Prime используйте несколько ключевых шагов, которые помогут грамотно и эффективно построить нужную модель.
1. Откройте Mathcad Prime и создайте новый документ.
2. Введите первое уравнение. Для этого используйте знак равенства (=), чтобы задать зависимость. Например, для уравнения \(x + y = 10\) на панели инструментов выберите поле ввода и напишите: x + y = 10.
3. Для записи следующего уравнения нажмите Enter для перехода на новую строку. Убедитесь, что символ равенства (=) правильно отображает зависимость. Пример второго уравнения: x - y = 2.
4. Чтобы обозначить несколько уравнений как систему, разделите их с помощью символа двоеточие («:») или просто вводите каждое уравнение на отдельной строке. Mathcad автоматически воспринимает несколько строк с уравнениями как систему, если уравнения векторные или матричные.
5. Если система включает несколько переменных, не забывайте указывать их явно в области определений, например, перед уравнениями. Используйте стрелки или подчеркивания для задания переменных и их значений, например: x := 5, y := 3.
6. Для решения системы уравнений используйте встроенные функции Mathcad. Выделите все уравнения, включая их определения, и примените команду решения, например, solve, чтобы найти значения переменных. Для этого введите: solve({x + y = 10, x - y = 2}, {x, y}).
7. После получения решения результат отобразится в виде числовых значений. Если решение не удается найти, проверьте корректность вводимых уравнений и ограничений, особенно на наличие ошибок в переменных.
8. Если нужно представить решение в графическом виде, используйте инструменты Mathcad для построения графиков, применяя такие функции, как plot, чтобы наглядно продемонстрировать зависимость между переменными.
9. После того как система уравнений решена, сохраните документ в подходящем формате для дальнейшего использования или анализа.
Эти шаги позволяют эффективно работать с системой уравнений в Mathcad Prime и быстро получить необходимые результаты.
Как начать работу с системой уравнений в Mathcad Prime
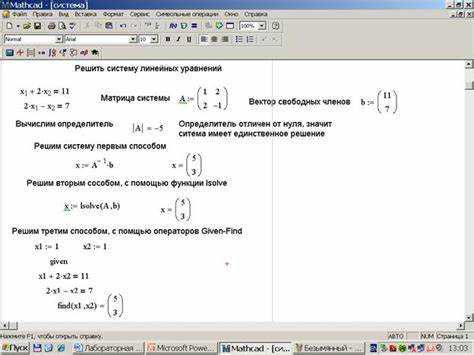
Для начала работы с системой уравнений в Mathcad Prime откройте программу и создайте новый документ. В панели инструментов выберите вкладку Вставка, а затем нажмите Уравнение. В появившемся окне введите нужные уравнения. Каждое уравнение пишется в отдельной строке, а для того чтобы связать их в систему, используйте символы «=» или «→».
Mathcad Prime автоматически определяет структуру уравнений, включая переменные и коэффициенты. Чтобы решить систему, используйте оператор solve, который позволит программе выполнить вычисления. Введите его в строку под системой уравнений, указывая переменные, которые необходимо найти.
После того как уравнения введены, важно правильно настроить параметры для решения системы. В настройках можно выбрать тип решения (например, числовое или аналитическое) в зависимости от типа уравнений. Для числового решения используйте численные значения для переменных, для аналитического – символьное представление.
Если система линейная, используйте операторы для матриц. Mathcad Prime поддерживает работу с матрицами и операциями над ними, такими как умножение, деление, транспонирование и инвертирование. Для нелинейных уравнений потребуется применять функции поиска корней, такие как fsolve.
Важно помнить, что для корректной работы системы уравнений все переменные должны быть определены до начала решения. Для этого можно указать значения переменных в верхней части документа, чтобы Mathcad Prime знал их заранее. В противном случае программа не сможет корректно выполнить решение.
В случае, если система уравнений имеет несколько решений, Mathcad Prime выведет все возможные варианты, которые соответствуют заданным условиям. Если решения не существует, программа сообщит об этом и предложит корректировки.
После получения решения системы уравнений, можно использовать результаты для дальнейших вычислений или визуализаций, например, построить графики зависимостей.
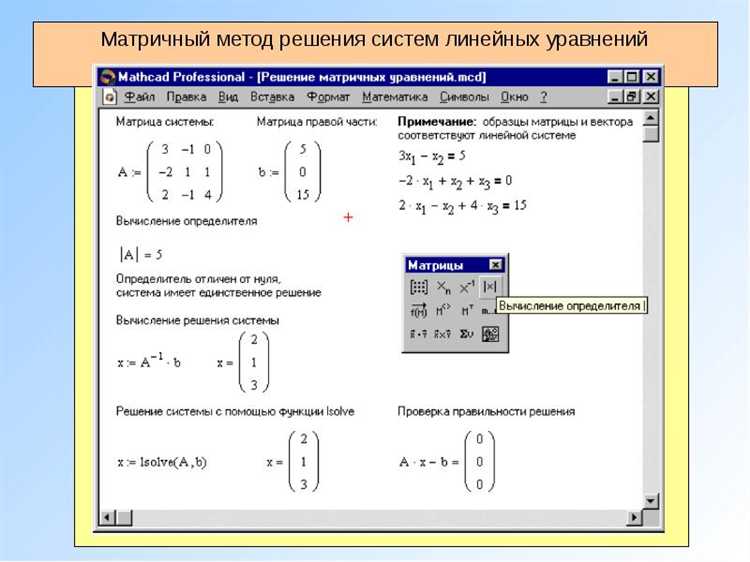
Создание матрицы для записи системы уравнений
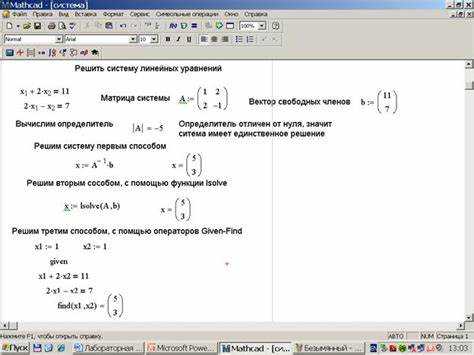
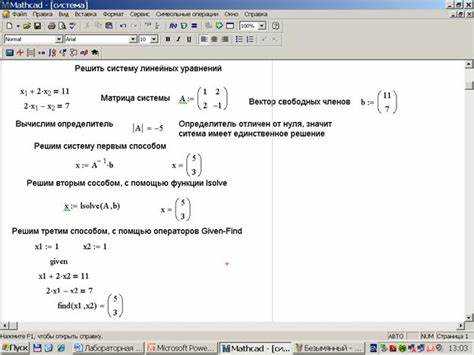
Для удобной записи системы линейных уравнений в Mathcad Prime, следует использовать матрицы. Матрицы позволяют компактно выразить систему уравнений в одном объекте, облегчая дальнейшие вычисления и анализ. Рассмотрим процесс создания матрицы в Mathcad Prime для записи системы уравнений.
1. Для начала создайте переменные для коэффициентов уравнений. Например, пусть система состоит из трех уравнений с тремя переменными. Обозначим коэффициенты как a1, a2, a3, … и соответствующие переменные как x1, x2, x3, ….
2. Перейдите к созданию самой матрицы. Для этого используйте квадратные скобки [ ] для обозначения элементов. Например, для записи матрицы коэффициентов, содержащей три уравнения и три переменные, можно использовать следующую конструкцию:
A := [[a1, a2, a3], [b1, b2, b3], [c1, c2, c3]]
Здесь каждая строка матрицы соответствует одному уравнению, а каждый элемент строки – коэффициент перед переменной в уравнении.
3. Создание вектора переменных также достаточно просто. Вектор можно представить как столбец:
X := [x1, x2, x3]
4. Запись правых частей уравнений осуществляется аналогично. Для этого создайте еще один вектор, который будет хранить значения правых частей уравнений:
B := [b1, b2, b3]
5. После того как матрица коэффициентов, вектор переменных и вектор правых частей определены, система уравнений принимает вид:
A * X = B
Теперь можно решать эту систему с помощью встроенных функций Mathcad Prime. Использование матричного представления ускоряет процесс вычислений и облегчает последующие шаги для получения решений.
Не забывайте, что размерность матрицы и векторов должна соответствовать количеству переменных и уравнений в системе. При неправильной размерности Mathcad Prime не сможет выполнить операцию умножения или решить систему уравнений.
Добавление переменных и коэффициентов в уравнения
Для работы с уравнениями в Mathcad Prime необходимо сначала определить переменные и коэффициенты, которые будут использоваться в расчетах. Добавление переменных в уравнения выполняется через интерфейс программы, где можно задать значения и их типы, а также использовать их в дальнейших вычислениях.
Чтобы добавить переменную, достаточно ввести ее имя и присвоить ей значение. Например, для задания переменной \( x \) с значением 5, необходимо ввести в рабочую область:
x := 5
Mathcad Prime поддерживает использование как числовых значений, так и символических переменных. Для задания символической переменной, которая будет использоваться в уравнениях, достаточно ввести просто имя переменной без присваивания конкретного значения. Например, можно задать переменную \( a \) для коэффициента уравнения:
a
После этого переменная \( a \) будет доступна для использования в любых уравнениях, где требуется коэффициент.
Для задания коэффициентов в уравнениях также используются символы. Если нужно задать коэффициент в уравнении, достаточно указать его в нужной части выражения. Например, для линейного уравнения \( y = ax + b \), где \( a \) и \( b \) – это коэффициенты, можно записать:
y := a * x + b
Значения переменных \( a \), \( b \), и \( x \) можно изменять непосредственно в уравнении, при этом Mathcad Prime автоматически пересчитает результат в зависимости от новых значений.
Для более сложных уравнений и систем переменных можно использовать подстановку значений в отдельные части уравнений, а также создавать массивы значений для переменных. Например, чтобы создать массив коэффициентов для полинома, можно ввести:
coefficients := {a, b, c}
Затем использовать его в уравнении, подставив коэффициенты по индексу:
y := coefficients[1] * x^2 + coefficients[2] * x + coefficients[3]
Таким образом, можно эффективно управлять переменными и коэффициентами, создавая сложные выражения и вычисления в Mathcad Prime. Убедитесь, что все переменные и коэффициенты корректно заданы, чтобы избежать ошибок при вычислениях.
Использование операторов для решения системы уравнений
Оператор solve позволяет решить систему уравнений с несколькими переменными. Для его использования необходимо задать уравнения в виде списка и указать переменные, относительно которых нужно найти решения. Например, для системы уравнений:
x + y = 5 2x - y = 1
Задача решается с помощью оператора solve следующим образом:
solve({x + y = 5, 2x - y = 1}, {x, y})
Результатом будет решение системы, где Mathcad найдет значения для переменных x и y.
Для более сложных систем или нелинейных уравнений Mathcad предоставляет оператор fsolve, который используется для численного решения нелинейных систем. Важно понимать, что fsolve требует начальных приближений для переменных. Например, для системы уравнений:
x^2 + y^2 = 4 x + y = 1
Применение fsolve будет следующим:
fsolve({x^2 + y^2 = 4, x + y = 1}, {x, y}, {x = 1, y = 0})
Здесь {x = 1, y = 0} – это начальное приближение. Оператор fsolve позволяет найти приближенное решение системы.
Кроме того, для решения системы с параметрами или функциями можно использовать оператор symbolic solve, который позволяет работать с аналитическими решениями. Для этого необходимо определить уравнение как символьное и решить его. Например:
solve(x^2 + y^2 = 4, {x, y})
В этом случае Mathcad вычислит общее аналитическое решение системы.
При решении системы с использованием операторов важно учитывать точность начальных данных и специфику самих уравнений, чтобы избежать ошибок в вычислениях. В случае использования fsolve следует тщательно выбирать начальные приближения, так как неправильный выбор может привести к некорректным результатам.
Проверка корректности введённых данных и решений
После ввода системы уравнений в Mathcad Prime важно убедиться в правильности исходных данных и полученных решений. Это помогает избежать ошибок в дальнейшем расчёте и гарантирует, что результат будет точным и надёжным.
Для проверки корректности введённых данных и решений можно использовать несколько методов:
- Проверка синтаксиса: Mathcad Prime автоматически проверяет корректность математических выражений при их вводе. Однако стоит уделить внимание возможным опечаткам в названии переменных или знаков операции. Например, иногда знак «минус» может быть воспринят как «минус в качестве оператора вычитания», а не как часть числа.
- Проверка единиц измерений: Если система уравнений связана с физическими величинами, важно убедиться, что все данные введены с правильными единицами измерения. Mathcad Prime позволяет указать единицы для каждой переменной, и система автоматически выполнит преобразование единиц, если это необходимо.
- Проверка граничных условий: Если в уравнениях есть параметры с ограничениями (например, значения переменных не могут быть отрицательными), стоит вручную проверять, что они не выходят за пределы допустимых значений. В Mathcad Prime можно добавить условия для проверки, чтобы программа предупредила о возможных ошибках.
Для проверки решений системы уравнений следует:
- Подставить решения обратно в исходные уравнения: После нахождения решений важно подставить их в исходные уравнения и проверить, что оба уравнения выполняются. Это поможет убедиться в правильности найденных значений переменных.
- Анализировать полученные результаты: Важно проверить, соответствуют ли результаты логическим и физическим ограничениям задачи. Например, если в задаче рассматривается скорость, то полученное решение не должно быть отрицательным.
- Использование численных методов для верификации решений: Для более сложных уравнений можно применить численные методы, такие как метод Ньютона или метод подбора. Это позволит получить приближённые решения и сравнить их с аналитическими.
- Проверка на устойчивость решений: Важно проверять, насколько сильно решение зависит от изменений в исходных данных. Для этого можно выполнить небольшие изменения значений переменных и посмотреть, как изменится результат.
Системы уравнений в Mathcad Prime легко проверяются с помощью встроенных инструментов, но важнейшее значение имеет внимательность к деталям на всех этапах работы. Всегда проверяйте введённые данные и анализируйте полученные решения для повышения точности расчётов.
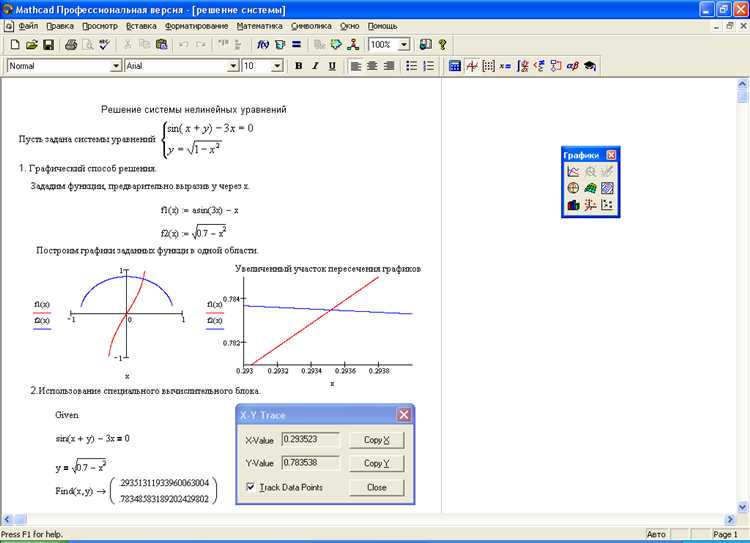
Графическое представление решений системы уравнений в Mathcad Prime

В Mathcad Prime графическое представление решений системы уравнений позволяет наглядно проиллюстрировать поведение решений в зависимости от параметров. Для этого используются графики, отображающие зависимости переменных и их пересечения, что помогает визуализировать возможные решения системы. Рассмотрим, как построить график для системы уравнений.
1. Для начала откроем Mathcad Prime и создадим новый рабочий лист. Введите уравнения системы в виде выражений. Например, рассмотрим систему из двух уравнений:
x + y = 3 2x - y = 1
2. Чтобы построить график, необходимо выразить одно уравнение относительно одной из переменных. Пусть для первого уравнения выразим y:
y = 3 - x
Для второго уравнения:
y = 2x - 1
3. Теперь создадим график для обеих функций. Для этого используем команду plot и указываем диапазоны значений для x. Например, пусть x будет от -5 до 5:
plot(x, y1(x), y2(x), x = -5..5)
Где y1(x) и y2(x) – это функции, определённые выше. Mathcad Prime автоматически отобразит оба графика на одном рисунке. Для точного отображения точек пересечения можно использовать дополнительные опции графика.
4. Для нахождения точек пересечения графиков можно воспользоваться инструментами решения уравнений или численного поиска. В Mathcad Prime можно использовать функцию solve для поиска значений переменных при которых уравнения равны:
solve(y1(x) = y2(x), x)
5. После нахождения точек пересечения можно дополнительно выделить их на графике, чтобы наглядно показать решения системы. Для этого в настройках графика можно добавить маркеры в точках пересечений.
6. Если система содержит более двух уравнений или требуется графическое представление в многомерном пространстве, можно использовать 3D-графики, применяя команду plot3d для визуализации решений в трёх измерениях. Например, для системы из трёх уравнений:
x + y + z = 6 2x - y + z = 4 3x + 2y - z = 5
Для построения графика в трехмерном пространстве можно использовать:
plot3d(x, y, z)
Графическое представление решений системы уравнений в Mathcad Prime эффективно визуализирует результаты, позволяет быстро определить пересечения и понять, как изменяются решения при изменении параметров. Это особенно полезно для анализа нелинейных систем или систем с множественными решениями.
Вопрос-ответ:
Как начать вводить систему уравнений в Mathcad Prime?
Чтобы начать вводить систему уравнений в Mathcad Prime, сначала нужно открыть программу и создать новый документ. Затем выберите подходящее место для ввода уравнений. Для этого используйте клавишу «Insert», чтобы добавить строку ввода. Введите уравнения, разделяя их оператором «равно» (=) и используйте точку с запятой (;) для разделения нескольких уравнений в одной строке.
Как правильно использовать переменные в системе уравнений Mathcad Prime?
Для работы с переменными в Mathcad Prime просто вводите имя переменной, после чего указывайте её значение или выражение, которому она соответствует. Например, можно задать переменную x как x := 5, и затем использовать её в уравнениях системы. Если переменные являются неизвестными, их можно оставить неинициализированными, и Mathcad Prime будет искать их значения при решении системы уравнений.
Как решить систему уравнений в Mathcad Prime?
Чтобы решить систему уравнений в Mathcad Prime, воспользуйтесь встроенной функцией «solve». Для этого выделите уравнение или систему уравнений и используйте функцию «Solve» для нахождения решения. Убедитесь, что все переменные в системе имеют нужные значения или заданы как неизвестные. После этого Mathcad Prime автоматически выполнит решение и выведет результат в виде числовых значений или выражений.
Какие ошибки могут возникнуть при вводе системы уравнений в Mathcad Prime?
Одной из распространённых ошибок является неправильный синтаксис при вводе уравнений. Например, если забыть поставить точку с запятой или неправильно записать операторы, программа не сможет корректно интерпретировать уравнения. Также важно убедиться, что все переменные заданы верно и используются в правильном контексте. Если система уравнений не имеет решений или содержит логические ошибки, Mathcad Prime предупредит об этом и предложит варианты исправления.
Как можно оформить вывод решения системы уравнений в Mathcad Prime?
Mathcad Prime позволяет настраивать вывод решения системы уравнений с помощью различных форматов. Для этого можно использовать текстовые поля для пояснений, а также графическое отображение решений через графики. Чтобы оформить решение, добавьте текстовый блок или графическое поле, в которое вставьте результаты расчётов. Таким образом, можно создать ясное и наглядное представление для дальнейшего анализа.
Как записать систему уравнений в Mathcad Prime?
Для того чтобы записать систему уравнений в Mathcad Prime, нужно выполнить несколько шагов. Сначала откройте программу и создайте новый документ. Затем используйте символы для записи уравнений, например, знак равенства (:=) для присваивания значений переменным. Чтобы ввести систему уравнений, можно использовать операторы переноса строки или сразу записывать все уравнения в одной строке, разделяя их точкой с запятой. Важно учитывать правильность синтаксиса для каждого уравнения. После ввода системы уравнений можно использовать функции и операторы для дальнейших вычислений и анализа.