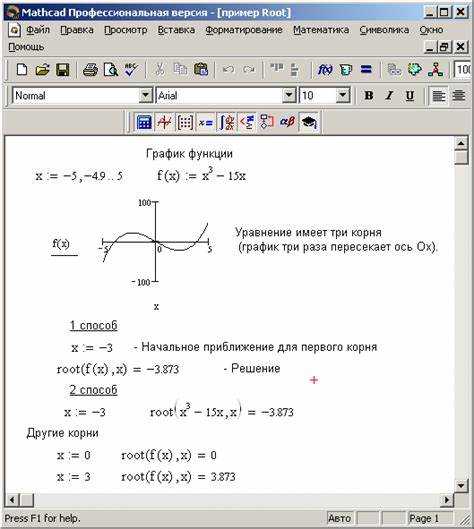
Функция root в Mathcad предназначена для нахождения корней уравнений и систем уравнений с высокой точностью. Она реализует численные методы решения, позволяя определить значения переменных, при которых заданное выражение равно нулю. Важной особенностью функции является возможность работать как с одной переменной, так и с вектором неизвестных.
Применение root оправдано в задачах, где аналитическое решение затруднено или невозможно. Например, при поиске корней нелинейных уравнений, определении устойчивых точек в динамических системах, а также в инженерных расчетах, связанных с оптимизацией и моделированием. Функция поддерживает настройку начального приближения, что существенно влияет на сходимость и скорость решения.
Для эффективного использования root важно корректно задавать функцию, описывающую уравнение, и обеспечивать адекватное начальное приближение. Рекомендуется избегать точек с неопределённостями и разрывами, что может привести к ошибкам или отсутствию сходимости. В Mathcad функция root интегрирована в вычислительную среду, позволяя сразу использовать найденные корни в последующих расчетах и визуализациях.
Как использовать root для поиска корней уравнений в Mathcad
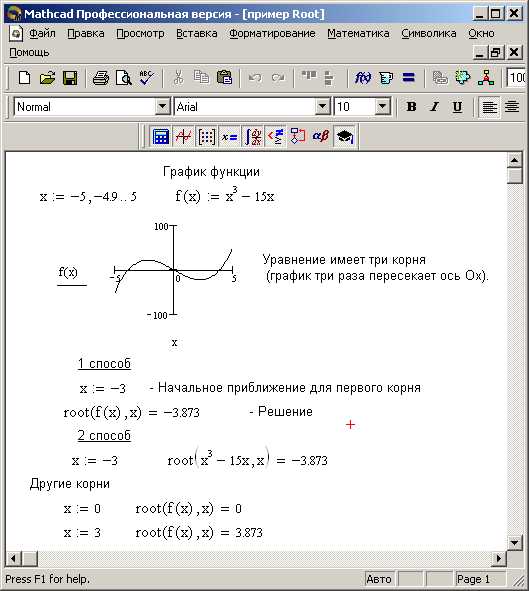
Функция root в Mathcad служит для численного поиска корней уравнений, заданных одной переменной. Основной синтаксис включает передачу уравнения и начального приближения для решения.
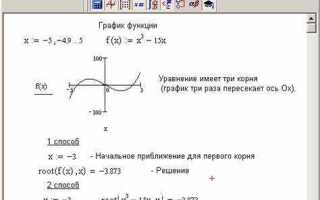
Пример вызова: root(f(x), x, x0), где f(x) – выражение, корень которого ищется, x – переменная, x0 – начальное приближение. Mathcad применяет итерационные методы, начиная с x0, для нахождения решения.
Для повышения точности следует выбирать начальное приближение близким к предполагаемому корню. При сложных уравнениях можно предварительно построить график функции и определить диапазон, где root будет эффективен.
Если уравнение зависит от параметров, их значения нужно задавать до вызова функции. Рекомендуется использовать переменные с четкими именами для повышения читаемости формул.
Функция root возвращает первое найденное значение, удовлетворяющее уравнению с заданной точностью. При отсутствии корня вблизи x0 результат может быть неверным или отсутствовать.
Для решения систем уравнений применяется функция root с векторными аргументами или другие специализированные методы Mathcad.
Определение начальных приближений для функции root
Функция root в Mathcad решает нелинейные уравнения численно, используя метод Ньютона или секущих. От правильного выбора начального приближения зависит сходимость и скорость вычисления корня. Начальное приближение должно находиться достаточно близко к искомому корню, чтобы избежать расходимости или попадания в посторонние корни.
Рекомендуется анализировать график функции или использовать аналитические оценки для выбора начальной точки. При работе с многочленами начальное приближение можно брать в интервале, где функция меняет знак. Если корней несколько, лучше запускать root с разными приближениями, чтобы найти все решения.
В задачах с параметрами следует проверять чувствительность результата к начальному приближению – если корень сильно зависит от точки старта, стоит провести предварительный перебор или использовать встроенные методы Mathcad для уточнения интервала.
Для уравнений, заданных сложными функциями, полезно применять приближения, основанные на физических или практических соображениях задачи, что уменьшает число итераций и повышает точность результата.
Решение систем нелинейных уравнений с помощью root
В Mathcad функция root эффективно применяется для численного решения систем нелинейных уравнений. Для этого необходимо задать систему в виде векторной функции, где каждое уравнение выражается через отдельный элемент вектора. Далее root используется для поиска вектора переменных, при котором все уравнения системы равны нулю.
Ключевой момент – корректное задание начального приближения. Оно должно быть близко к реальному решению, иначе итерационный процесс может не сойтись или привести к локальному экстремуму. Начальное приближение задается в виде вектора с тем же числом элементов, что и количество уравнений в системе.
Пример использования root для системы из двух уравнений: создается функция, возвращающая вектор значений левой части уравнений, и вызывается root с начальным вектором переменных. Mathcad автоматически применяет численные методы, такие как метод Ньютона или секущих, для нахождения решения.
При работе с системами важно контролировать сходимость решения. Для этого можно использовать параметры точности, задаваемые в Mathcad, а также анализировать изменение значений функции на каждом шаге. В случае отсутствия сходимости рекомендуется изменить начальное приближение или пересмотреть постановку системы.
root в Mathcad также позволяет решать системы с параметрами, фиксируя одни переменные и решая систему по другим. Такой подход полезен для анализа зависимости решения от параметров.
Применение root при анализе математических моделей
Функция root в Mathcad служит для нахождения корней уравнений и систем уравнений, что критично при исследовании поведения математических моделей. В прикладных задачах root позволяет определять устойчивые состояния, точки равновесия и критические параметры моделей.
Основные направления использования root в анализе моделей:
- Поиск стационарных решений. В динамических системах root помогает вычислить точки, где производная равна нулю, что соответствует состояниям равновесия.
- Определение параметров, обеспечивающих заданные условия. Например, при моделировании процессов оптимизации root позволяет вычислить параметры, при которых достигается минимум или максимум функции.
- Решение нелинейных уравнений и систем. Многие модели содержат нелинейные зависимости, для которых аналитические решения отсутствуют. Root обеспечивает численное решение таких уравнений с заданной точностью.
Рекомендации по применению root в Mathcad при анализе моделей:
- Перед использованием root необходимо задать адекватное начальное приближение, так как функция чувствительна к выбору стартовой точки и может сходиться к локальному корню.
- При работе с системами уравнений использовать root с векторными переменными, что позволяет одновременно решать несколько взаимосвязанных уравнений.
- Проводить проверку полученных корней путем подстановки в исходные уравнения для оценки точности решения.
- Использовать root совместно с визуализацией – графики функций помогают выявить количество корней и их приближённые местоположения.
- Для повышения надёжности решений применять параметры функции root, регулирующие точность и максимальное число итераций, адаптируя вычисления под сложность модели.
Применение root обеспечивает быстрый и точный численный анализ, что существенно ускоряет процесс верификации и оптимизации математических моделей в инженерии, экономике и науке.
Обработка ошибок и сходимость при использовании root
Mathcad автоматически контролирует точность вычисления корня, используя критерии сходимости, такие как малое изменение значений между итерациями или достижение заданного предела погрешности. При превышении максимального количества итераций или отсутствии сходимости возвращается ошибка. В этом случае целесообразно изменить начальное приближение, пересмотреть постановку задачи или увеличить допустимую погрешность.
Особое внимание следует уделять уравнениям с несколькими корнями или с особенностями – разрывами, экстремумами, сложной поведением функции. В таких случаях целесообразно разбивать область поиска на участки и вызывать root для каждого из них отдельно. Это снижает риск ошибки из-за попадания в неподходящую область сходимости.
Для контроля результата рекомендуется сравнивать полученный корень с графическим представлением функции и проводить дополнительную проверку через подстановку решения в исходное уравнение. Если модуль значения функции в найденной точке не удовлетворяет требуемой точности, стоит повторить вычисления с другим начальным значением или изменить настройки root.
Использование root для численного решения уравнений с параметрами

Функция root в Mathcad позволяет решать уравнения, содержащие параметры, при заданных значениях этих параметров. Такой подход облегчает анализ зависимости корней от параметрических изменений и ускоряет численное моделирование.
- Для решения уравнения с параметрами необходимо сначала определить параметры и задать их численные значения.
- В уравнении root выступает как оператор поиска корня по основной переменной, тогда как параметры остаются фиксированными.
- Рекомендуется использовать начальное приближение, близкое к ожидаемому решению, чтобы ускорить сходимость алгоритма.
Пример:
root(x^2 + a*x + b = 0, x, x0)где a и b – параметры, x0 – начальное приближение. Изменяя a и b, можно получить зависимость корня от параметров.
- При анализе нескольких параметров рекомендуется создавать таблицы значений параметров и вычислять корни в цикле, используя root в сочетании с функциями перебора.
- Для уравнений с несколькими корнями следует уточнять начальное приближение, чтобы получить нужный корень.
- Если параметры изменяются непрерывно, можно использовать root в сочетании с графическим отображением корней для наглядного анализа.
Таким образом, root позволяет эффективно решать уравнения с параметрами, обеспечивая точный численный результат и гибкость при исследовании влияния параметрических изменений.
Особенности работы root с комплексными числами
Для комплексного числа z = re^{iθ} корни вычисляются по формуле:
root(z, n) = r^{1/n} \cdot e^{i(\frac{θ + 2k\pi}{n})}, k = 0, 1, …, n-1.
Важно помнить, что Mathcad возвращает все эти значения одновременно, поэтому дальнейшие вычисления с результатом требуют выбора конкретного корня. Например, для извлечения главного корня следует обращаться к первому элементу результата (root(z, n)[0]).
При работе с корнями комплексных чисел следует учитывать, что аргумент числа задается в диапазоне от -π до π, что влияет на расположение корней и может приводить к неожиданным сдвигам при переходе через ветвь аргумента.
Рекомендуется использовать функцию abs для контроля модуля и arg для проверки аргумента комплексного результата, чтобы избежать ошибок при интерпретации полученных корней.
Также при программировании вычислений с root комплексных чисел целесообразно предусматривать обработку всех корней, особенно в задачах, где важна полная картина решений, например, в уравнениях с комплексными коэффициентами.
Примеры практических задач с применением root в инженерии
В инженерных расчетах функция root в Mathcad используется для поиска корней уравнений, возникающих при моделировании сложных систем. Например, при анализе прочности конструкций часто требуется решить нелинейное уравнение напряжений для определения критической нагрузки. Здесь root позволяет получить точное значение нагрузки, при которой материал начинает деформироваться пластично.
В гидравлике функция root помогает определить скорость потока жидкости, решая уравнения движения с учетом сопротивления трубопроводов и изменения давления. Практическое применение – расчет диаметра трубы для заданного расхода и минимизации потерь энергии.
При проектировании электрических цепей root используется для нахождения значений сопротивления или емкости, обеспечивающих устойчивую работу фильтров и усилителей. Например, решая уравнения с комплексными коэффициентами, можно оптимизировать параметры цепи под требуемую частоту среза.
В термодинамике функция root помогает определить температуру или давление в системах с фазовыми переходами, решая уравнения состояния вещества. Пример – вычисление точки кипения в смеси с несколькими компонентами, где аналитическое решение невозможно без численных методов.
Для динамического анализа механизмов root применяется при расчете собственных частот колебаний, что критично для предотвращения резонансных нагрузок. Задача сводится к поиску корней характеристического уравнения, заданного матрицей масс и жесткостей системы.
Рекомендации по использованию root в Mathcad: важно задавать начальные приближения, основанные на физической интерпретации задачи, чтобы ускорить сходимость решения и избежать ложных корней. Для сложных уравнений стоит применять разбиение на интервалы и проверять знак функции на границах, что повышает надежность результатов.
Вопрос-ответ:
Для чего используется функция root в Mathcad?
Функция `root` в Mathcad применяется для нахождения корней уравнений. Она позволяет найти значение переменной, при котором заданное уравнение становится равным нулю. Это удобно при решении уравнений, которые невозможно аналитически выразить через известные функции. В отличие от символьного решения, `root` работает численно, то есть подбирает приближённое значение, удовлетворяющее условию с заданной точностью.
Как правильно задать начальное приближение для функции root?
Начальное приближение нужно выбрать так, чтобы оно было как можно ближе к предполагаемому корню. Это помогает избежать сходимости к нежелательному корню или отсутствия решения. Если функция имеет несколько корней, выбор начальной точки может привести к нахождению любого из них. В некоторых случаях рекомендуется построить график уравнения и визуально определить, где находится нужный корень, а уже затем задать соответствующее приближение.
Можно ли с помощью root решать системы уравнений?
Функция `root` в чистом виде применяется к одиночным уравнениям. Для решения системы нелинейных уравнений в Mathcad используется функция `find`, которая работает в сочетании с оператором `Given`. Однако можно применять `root` к каждому уравнению по отдельности, если они не связаны между собой. В случае связанных уравнений лучше использовать специализированные численные методы, встроенные в Mathcad.
Что произойдёт, если в функцию root передать уравнение без действительного корня?
Если уравнение не имеет действительных решений, Mathcad не сможет найти корень, и в результате будет выведено сообщение об ошибке. Например, при попытке найти корень уравнения \(x^2 + 1 = 0\), программа сообщит о невозможности решения, поскольку функция root работает только с действительными числами. В таких случаях следует проверить область определения и поведение функции на интервале поиска.
Можно ли использовать функцию root для поиска корней уравнения, содержащего пользовательские функции?
Да, функция `root` поддерживает уравнения, в которых участвуют пользовательские функции. Главное, чтобы такие функции были корректно определены и возвращали численные значения при подстановке аргумента. Это расширяет возможности Mathcad, позволяя искать корни уравнений с более сложной логикой, заданной пользователем, например, через циклы, условия или вызовы других функций.