Как задать кусочную функцию в mathcad

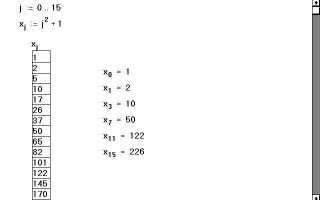
В среде Mathcad реализация кусочной функции возможна с использованием встроенной конструкции if. Это позволяет задать различные выражения в зависимости от значения аргумента. Основной подход – последовательное применение условий внутри тела функции, что обеспечивает вычисление нужного фрагмента.

Для определения кусочной функции следует использовать формат:

f(x) := if x < a, выражение1, if x < b, выражение2, выражение3

Каждое условие проверяется последовательно. Как только одно из них выполняется, соответствующее выражение используется в качестве результата. Важно учитывать, что Mathcad оценивает условия слева направо, поэтому порядок имеет значение. Использование вложенных условий позволяет задать функции с любым количеством фрагментов.

При работе с кусочными функциями важно убедиться, что все участки определения охватывают всю возможную область аргумента. В противном случае Mathcad может вернуть ошибку «This value must be a number» при вычислении функции вне заданных условий.

Для повышения читаемости и стабильности рекомендуется использовать логические операторы and и or при необходимости задать диапазоны значений в условиях. Это особенно актуально при моделировании технических или физических процессов, где границы важны для корректности расчётов.

Как задать простую кусочную функцию с двумя условиями

В Mathcad для определения кусочной функции с двумя условиями используется оператор if. Пример: задать функцию f(x), равную x² при x < 0 и 2x при x ≥ 0.

Объявите функцию следующим образом:

f(x) := if x < 0, x², 2·x

Первый аргумент – условие. Второй – результат при выполнении условия. Третий – альтернатива, если условие ложно. Символ «:=» – оператор определения функции.

Убедитесь, что запятые разделяют аргументы, а не точки с запятой. Mathcad воспринимает только запятую как разделитель в конструкции if.

При вводе выражений используйте редактор Mathcad: вводите if с клавиатуры, затем используйте встроенные поля для условия и значений. Это предотвратит синтаксические ошибки.

Для проверки корректности используйте панель «Math» – если функция введена правильно, подсветка синтаксиса отсутствует.

Использование логических операторов для построения условий

Для определения кусочной функции в Mathcad критически важно грамотно использовать логические операторы. Основные операторы: <, <=, >, >=, = и ∧, ∨ (вводятся как Ctrl+Shift+A и Ctrl+Shift+O соответственно).

Условие типа x < 0 возвращает 1 при выполнении и 0 в противном случае. Это позволяет описывать функции вида f(x) := (x < 0) * выражение1 + (x >= 0) * выражение2. Mathcad интерпретирует логическое выражение как числовой множитель: если условие истинно, результат учитывается; если ложно – обнуляется.

Для задания диапазона значений применяются логические связки. Пример: (x > 0) ∧ (x <= 5) ограничивает интервал от 0 до 5, не включая 0. Такая конструкция критична при построении непрерывных участков кусочной функции.

Важно избегать перекрытия условий. Если выражения пересекаются, Mathcad может вернуть сумму нескольких веток, что приведёт к ошибочному результату. Проверяйте, чтобы каждое условие охватывало строго определённую область определения функции.

Для повышения читаемости используйте промежуточные определения логических условий. Например: A := x < 0, B := (x >= 0) ∧ (x < 5). Затем в основной формуле: f(x) := A * выражение1 + B * выражение2 + ....

При необходимости описания дискретных значений используйте строгое сравнение: x = 3. В отличие от других операторов, он не допускает отклонений и срабатывает только при точном совпадении.

Применение встроенной функции if для кусочной логики

В Mathcad функция if позволяет реализовать кусочную зависимость без необходимости строить сложные выражения через операторы определения функций. Синтаксис: if(условие, значение_если_истина, значение_если_ложь).

Для определения кусочной функции с несколькими диапазонами используйте вложенные конструкции if. Например, для определения функции:

{ x^2,        при x < 0
f(x) =    { 0,          при x = 0
{ √x,        при x > 0

В Mathcad:

f(x) := if(x < 0, x^2, if(x = 0, 0, sqrt(x)))

• Всегда проверяйте условия в порядке приоритета – от более строгих к более общим. В противном случае условие x > 0 может быть достигнуто раньше x = 0, и результат будет искажен.
• Избегайте цепочек из более чем 3–4 вложенных if – это ухудшает читаемость. Разбивайте выражения на вспомогательные функции.
• Используйте if только в тех случаях, где каждый диапазон выражается однозначным значением. Для более сложных ветвлений применяйте условные операторы совместно с логическими функциями and, or.

Важно: if в Mathcad – это функция, а не оператор, как в языках программирования. Она возвращает значение и может быть использована внутри других выражений, что позволяет создавать компактные кусочные зависимости.

Как избежать ошибок единиц измерения в кусочной функции

В Mathcad каждая ветвь кусочной функции должна иметь согласованные единицы измерения. Если хотя бы один участок функции возвращает значение с несовместимыми единицами, Mathcad выдаст ошибку «Несоответствие единиц».

Первое правило: используйте единицы измерения явно. Например, вместо v := 10 задавайте v := 10 м/с. Это позволяет Mathcad отслеживать размерности при вычислениях и предотвращает неочевидные ошибки.

Второе правило: проверяйте единицы всех выражений, возвращаемых в каждой ветви. Например, в условии if T < 273 then R := 10 Ом else R := 5 м произойдёт ошибка, так как Ом и метр несовместимы. Все возможные возвращаемые значения должны иметь одну и ту же размерность.

Третье правило: используйте встроенную функцию unitsOf() для диагностики. Пример: unitsOf(f(T)) покажет размерность возвращаемого значения функции f. Это удобно для отладки сложных кусочных зависимостей.

Четвёртое правило: избегайте операций, где результат имеет условно-бессмысленную размерность. Например, выражение x := if t > 0 then 5 м + 3 с else 8 Н синтаксически корректно (если привести все к одной размерности вручную), но физически некорректно. Mathcad такие случаи обычно блокирует, но иногда ошибка проявляется только в зависимости от контекста использования.

Пятое правило: перед использованием кусочной функции в расчетах с размерностями – проверяйте каждую ветвь на соответствие ожидаемым единицам результата. Упростите каждую ветвь до скалярной величины и проверьте, что размерность одинакова во всех случаях.

Создание кусочной функции с множеством диапазонов

Для задания кусочной функции в Mathcad с множеством диапазонов используется последовательная проверка условий через оператор if. Каждый диапазон описывается логическим выражением и соответствующим значением функции. Конструкция строится в виде вложенных блоков или с помощью оператора else if для удобства чтения и отладки.

Пример: требуется задать функцию f(x), принимающую различные значения в зависимости от диапазона x:

f(x) :=

  if x < -2, -1

  else if x < 0, x + 2

  else if x < 3, x²

  else if x ≤ 5, 2·x — 1

  else 0

Каждое условие проверяется сверху вниз до первого истинного. Используйте строгие и нестрогие операторы сравнения (например, <, ≤), чтобы точно определить границы. Диапазоны не должны пересекаться, иначе результат может быть неоднозначным. Для отладки удобно строить график функции на нужном интервале, чтобы визуально проверить корректность переходов между диапазонами.

Формулы можно упрощать за счёт использования встроенных функций, но логика разветвлений должна оставаться прозрачной. Все числовые константы и выражения должны быть проверены на корректность типов, особенно при работе с единицами измерения – несоответствие единиц вызовет ошибку.

Для функций с большим числом диапазонов избегайте чрезмерного вложения условий. Лучше выделить ключевые диапазоны и вынести их в отдельные вспомогательные функции для повышения читаемости и упрощения отладки.

Определение кусочной функции с использованием вложенных условий

В Mathcad для задания кусочной функции через вложенные условия применяется конструкция if с последовательной проверкой диапазонов аргумента. Такой подход позволяет точно определить значения функции на каждом интервале без необходимости использовать отдельные области определения.

Синтаксис вложенного условия выглядит следующим образом:

f(x) := if x < a then y1 else if x < b then y2 else y3

Здесь переменная x сравнивается с границами a и b, а для каждого диапазона задается соответствующее значение y1, y2 или y3.

Рекомендуется строго следить за порядком проверок: от наименьшего к большему, чтобы исключить пересечение интервалов и обеспечить корректное определение значения.

Пример кусочной функции с тремя ветвями:

f(x) := if x < 0 then -1
else if x < 5 then x^2
else 10

В этом случае:

• при x < 0 функция равна -1;
• при 0 ≤ x < 5 функция принимает значение квадрата аргумента;
• при x ≥ 5 функция равна 10.

Для сложных функций допускается использовать более глубокие вложения, но важно сохранять читаемость и избегать чрезмерной вложенности. В некоторых случаях целесообразно разбить функцию на несколько промежуточных выражений.

Также можно комбинировать вложенные условия с логическими операторами and и or для определения интервалов с помощью диапазонов:

f(x) := if (x >= 0) and (x < 5) then x^2
else if x < 0 then -1
else 10

Этот способ позволяет сделать проверку интервалов более явной и гибкой.

Итог: вложенные условия в Mathcad – эффективный инструмент для создания кусочных функций с чёткими интервалами и точным управлением значениями в каждой области.

Отображение графика кусочной функции в Mathcad

Для построения графика кусочной функции в Mathcad важно правильно задать функцию с помощью условий и использовать встроенные инструменты графиков.

1. Создайте функцию с условными операторами, применяя оператор if или piecewise. Например:

   f(x) := if x < 0 then x^2 else sqrt(x)

2. Убедитесь, что область определения функции покрывает все участки, указанные в условиях. Mathcad автоматически вычисляет значения функции по всем точкам на графике.
3. Выделите область на листе, где будет отображён график. Вставьте объект графика через меню Insert → Graph → X-Y Plot.
4. В поле оси X задайте интервал значений, например, x от -5 до 5. Можно использовать выражение для вектора, например: x := -5, -4.9 .. 5.
5. В поле оси Y укажите функцию f(x). Mathcad отобразит график с разрывами и переходами, соответствующими кусочным условиям.
6. Для улучшения визуализации:
   • Установите шаг дискретизации по оси X достаточно мелким, чтобы детали кусочных переходов были видны.
   • При необходимости добавьте отдельные графики для каждого куска функции с разными стилями линии.
   • Используйте настройку диапазона осей, чтобы исключить ненужные области.
7. Если функция задаётся с помощью нескольких выражений, можно объединить их через конструкцию piecewise:

   f(x) := piecewise(x < 0, x^2, 0 ≤ x < 2, 3*x, x ≥ 2, 5)

8. После построения графика проверьте соответствие отображения аналитическому виду функции, особенно в точках разрыва и перехода между кусками.

Соблюдение этих рекомендаций позволяет получать точные и наглядные графики кусочных функций в Mathcad без дополнительных манипуляций.

Проверка значений кусочной функции в точках разрыва

В Mathcad контроль значений функции в точках разрыва выполняется через последовательную проверку пределов слева и справа, а также значения функции в самой точке разрыва. Для точного анализа необходимо задать функцию с использованием условных операторов (if, else или when) и явно определить поведение на границах интервалов.

Первый шаг – вычислить значения функции с подходом к точке разрыва слева и справа. В Mathcad это реализуется подстановкой значений, приближенных к точке, например: если точка разрыва x₀, проверить f(x₀ - δ) и f(x₀ + δ) при малом δ (например, δ = 10⁻⁶). Значения должны совпадать с ожидаемыми пределами каждой части функции.

Второй этап – проверить значение функции в самой точке разрыва f(x₀). Если f(x₀) не совпадает с одним из пределов, это указывает на разрыв первого рода (скачок). Если совпадает, разрыв отсутствует, либо функция непрерывна по определению в этой точке.

При необходимости визуализации поведения вокруг точки разрыва целесообразно построить график с увеличением масштаба по оси x, ограничив область около x₀. Визуально можно выявить несоответствия или скачки, которые не всегда очевидны из численных значений.

Важный момент – для корректной проверки необходимо обеспечить точность вычислений Mathcad, избегая округлений и численных погрешностей. Рекомендуется использовать встроенные функции Mathcad для работы с малыми значениями и сравнения с точностью до заданного ε.

Таким образом, систематическая проверка значений функции слева, справа и в точке разрыва позволяет подтвердить тип и наличие разрыва в кусочной функции, обеспечивая корректность её определения и дальнейшего анализа в Mathcad.

Вопрос-ответ:

Как в Mathcad задать кусочную функцию с несколькими условиями?

В Mathcad для определения кусочной функции применяют оператор условий if-then-else. Каждое условие прописывается отдельно, и для разных интервалов переменной указываются соответствующие выражения. Например, можно использовать вложенные условия: если x меньше нуля — одна формула, если от нуля до одного — другая, и для значений больше одного — третья. Это позволяет гибко описать функцию с разными значениями на разных участках.

Можно ли в Mathcad создавать кусочные функции без использования встроенных операторов if?

Да, можно применить функцию piecewise, которая специально предназначена для создания функций с разными значениями на разных участках. Эта функция принимает пары: условие и значение, которое применяется при выполнении этого условия. Такой способ более наглядный и удобный при работе с несколькими участками функции.

Как проверить корректность заданной кусочной функции в Mathcad?

Для проверки можно построить график функции в заданном диапазоне и убедиться, что переходы между участками совпадают с ожидаемыми значениями. Также полезно подставить конкретные значения переменной, соответствующие разным условиям, и сравнить результат вычислений с ручными расчетами. Если результаты совпадают, функция определена правильно.

Какие ограничения существуют при работе с кусочными функциями в Mathcad?

Основное ограничение связано с тем, что при большом количестве условий функция может стать громоздкой и сложной для редактирования. Кроме того, для более сложных разрывных функций требуется внимательно следить за корректностью условий, чтобы не было перекрытия интервалов или пропусков. Также важно помнить, что Mathcad обрабатывает условия строго в порядке их записи, что влияет на итоговое значение функции.

Как задать кусочную функцию, зависящую от нескольких переменных, в Mathcad?

Для функций нескольких переменных в Mathcad также можно использовать условные операторы или функцию piecewise, прописывая условия, зависящие от обеих переменных. Например, можно определить значения функции в зависимости от того, в какой части двумерной области находятся переменные. При этом условия могут включать логические операции, объединяющие сравнения по разным переменным.

Как в Mathcad задать кусочную функцию с разными выражениями на разных участках?

В Mathcad для определения кусочной функции используют оператор условия if или конструкцию с несколькими условиями. Например, для функции, которая принимает значение x² при x ≤ 0 и 2x + 1 при x > 0, можно написать: f(x) := if x ≤ 0 then x² else 2*x + 1. Такой способ позволяет задавать разные формулы для разных интервалов переменной. Для более сложных случаев применяют вложенные условия или функцию piecewise, если она доступна в вашей версии Mathcad.