Кусочные функции в Matlab задаются с использованием логических выражений, которые определяют условия для каждой части функции. Основной способ – использование оператора .* для поэлементного умножения на логические маски. Это позволяет избежать циклов и сохранить векторизованную форму кода.
Пример базового синтаксиса: y = (x < 0).*f1 + (x >= 0 & x < 2).*f2 + (x >= 2).*f3. Здесь f1, f2 и f3 – выражения для разных участков определения функции, которые автоматически применяются к нужным диапазонам значений x.
Для повышения читаемости кода и упрощения отладки, рекомендуется выносить логические условия в отдельные переменные. Например: cond1 = x < 0;, cond2 = x >= 0 & x < 2;. Это особенно полезно при работе с более чем тремя интервалами.
Также можно использовать встроенную функцию piecewise из Symbolic Math Toolbox. Пример: f = piecewise(x < 0, x^2, x >= 0 & x < 2, sin(x), x >= 2, log(x)). Этот подход удобен при символьных вычислениях и последующем аналитическом анализе.
Важно следить за совместимостью размеров массивов и типами данных. Все выражения должны быть одинакового размера, иначе Matlab вернёт ошибку. Для предотвращения таких ситуаций используйте функцию zeros или nan как инициализатор перед формированием результирующего массива.
Как определить кусочную функцию с помощью анонимных функций

В MATLAB кусочную функцию можно задать через комбинацию логических выражений и анонимных функций. Основной приём – использование логических масок внутри выражения.
Пример: кусочная функция f(x), определённая как:
f(x) = x² при x < 0,
f(x) = sin(x) при 0 ≤ x ≤ π,
f(x) = ln(x) при x > π
Описывается следующим образом:
f = @(x) (x.^2).*(x < 0) + sin(x).*(x >= 0 & x <= pi) + log(x).*(x > pi);
Каждое слагаемое включает логическое условие и соответствующее выражение. Оператор .* обеспечивает поэлементное умножение: выражение вычисляется только там, где выполняется условие.
Чтобы избежать ошибок, необходимо убедиться, что функции определены во всём диапазоне. Например, log(x) не определена при x ≤ 0, поэтому такие значения автоматически обнуляются логическим фильтром.
Для проверки корректности определения используйте векторные входные данные:
x = linspace(-5, 10, 1000);y = f(x);
Визуализация:
plot(x, y); grid on;
Избегайте использования if внутри анонимных функций – они не поддерживают условные конструкции. Используйте только логические выражения и поэлементные операции.
При необходимости добавления новых участков, просто расширяйте выражение по аналогии, соблюдая порядок условий и корректный логический охват всей области определения.
Использование конструкции if-else для задания кусочной зависимости
В MATLAB конструкция if-else позволяет явно задать кусочную зависимость функции от переменной. Это особенно удобно при реализации функций, поведение которых меняется в зависимости от диапазона значений аргумента.
Рассмотрим пример: необходимо определить функцию f(x), которая задаётся по следующему правилу:
f(x) =
x², если x < 0
2x + 1, если 0 ≤ x < 5
10, если x ≥ 5
Реализация:
function y = f(x)
if x < 0
y = x^2;
elseif x < 5
y = 2*x + 1;
else
y = 10;
end
endВ этой форме каждый диапазон описывается строго, без перекрытия. Условие elseif x < 5 не требует повторной проверки x ≥ 0, поскольку первое условие уже исключает отрицательные значения. Это повышает читаемость и уменьшает вероятность логических ошибок.
Для векторизованных вычислений данная конструкция неэффективна. Если требуется применить кусочную функцию к вектору, используйте логические индексы или функцию arrayfun. Пример:
f = @(x) arrayfun(@(x) ...
(x < 0) * x^2 + ...
(x >= 0 && x < 5) * (2*x + 1) + ...
(x >= 5) * 10, x);Это позволяет корректно обработать массив входных значений без использования цикла for.
Применение оператора logical indexing для построения кусочной функции
Logical indexing в MATLAB позволяет точно задать значения функции на отдельных интервалах без использования условных конструкций. Это особенно удобно при построении кусочных функций, где каждое условие соответствует определённой формуле.
Для задания функции необходимо сначала определить вектор аргументов. Например, x = -10:0.1:10;. Далее создаются логические маски: idx1 = x < 0;, idx2 = x >= 0 & x <= 5;, idx3 = x > 5;.
Создаётся вектор значений: y = zeros(size(x));. Затем по маскам присваиваются значения: y(idx1) = -x(idx1).^2;, y(idx2) = 2*x(idx2) + 1;, y(idx3) = sqrt(x(idx3));.
Этот метод гарантирует одновременное выполнение всех условий без вложенных операторов if. Также исключаются ошибки, связанные с перекрытием интервалов или неполным покрытием области определения.
Logical indexing легко масштабируется. Добавление новых участков функции требует только определения дополнительной маски и соответствующего выражения. Это делает код компактным, читаемым и легко отлаживаемым.
Создание кусочной функции с помощью функции piecewise из Symbolic Math Toolbox
Для определения кусочной функции в Matlab используется функция piecewise из пакета Symbolic Math Toolbox. Она позволяет задать выражения, зависящие от условий, без необходимости вручную реализовывать логические проверки.
Перед использованием необходимо создать символьную переменную: syms x. Затем формируется выражение с помощью piecewise(условие1, значение1, условие2, значение2, ..., значение_иначе). Последний аргумент – значение по умолчанию, если не выполняется ни одно из условий.
Пример: f = piecewise(x < 0, -1, x >= 0 & x < 1, x^2, x >= 1, 1). Эта функция возвращает -1 при x < 0, x^2 на интервале от 0 до 1 (не включая 1), и 1 при x ≥ 1.
Для упрощения и анализа используйте simplify(f) и pretty(f). Для построения графика примените fplot(f, [a b]), где [a b] – интервал отображения. Для подстановки значения используйте subs(f, x, число).
Функция piecewise сохраняет символьную природу выражения, что позволяет проводить дифференцирование (diff), интегрирование (int) и упрощение (simplify) без потери структуры условий.
Графическое отображение кусочной функции с использованием plot и fplot
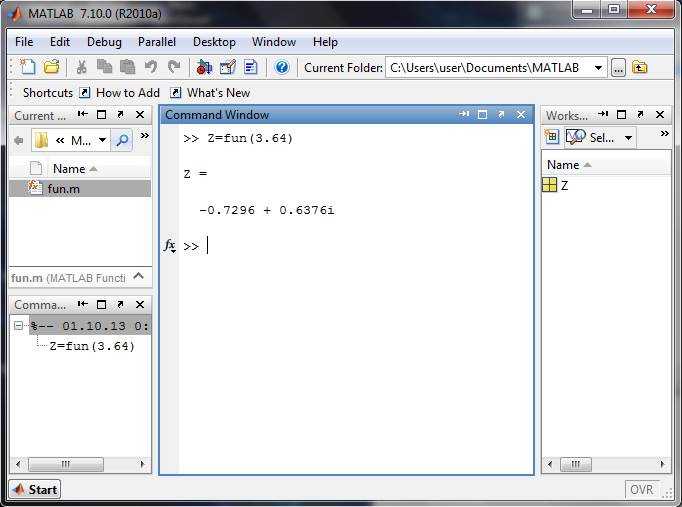
Для визуализации кусочной функции в MATLAB необходимо точно задать интервалы определения каждой части функции и обеспечить согласованное отображение на одном графике. Использование plot и fplot зависит от способа задания функции: аналитически или через массивы данных.
При использовании plot сначала формируются отдельные векторы значений x и y для каждого участка. Например:
x1 = -5:0.1:0;
y1 = x1.^2;
x2 = 0.1:0.1:5;
y2 = 2*x2 + 1;
plot(x1, y1, 'b', x2, y2, 'r')
grid on
Каждый участок отображается своим цветом или стилем линии. Интервалы не должны пересекаться, чтобы избежать ложных разрывов или наложений. Если функция определена не во всех точках, нужно использовать NaN для пропуска, иначе MATLAB соединит несвязанные точки прямыми линиями.
Для аналитически заданных кусочных функций предпочтительнее fplot с использованием анонимной функции и конструкции if...else или piecewise:
f = @(x) (x < 0).*x.^2 + (x >= 0).*(2*x + 1);
fplot(f, [-5, 5], 'LineWidth', 1.5)
grid on
fplot автоматически подбирает точки, обеспечивая гладкий график без необходимости задавать шаг. При необходимости повышения точности можно использовать опцию 'MeshDensity'.
Для отображения разрывов полезно добавлять вертикальные линии с помощью xline, чтобы подчеркнуть изменение формулы функции на границе:
xline(0, '--k')
Если функция содержит разрывы первого рода, plot предпочтительнее, так как позволяет вручную управлять отрисовкой каждого участка с контролем включения или исключения граничных точек.
Обработка ошибок при задании кусочной функции на пересекающихся интервалах
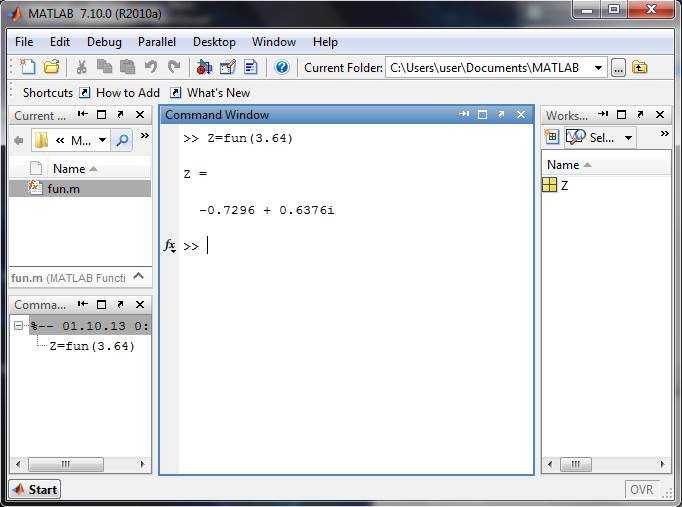
Пересечение интервалов при определении кусочной функции в Matlab приводит к неоднозначности и неправильным вычислениям. Важно контролировать границы участков и их взаимное расположение до реализации функции.
- Проверка пересечений. Перед созданием функции необходимо убедиться, что интервалы не накладываются. Для этого используют проверку на пересечение: если интервал
[a,b]пересекается с[c,d], то условиеmax(a,c) < min(b,d)указывает на конфликт. - Использование строгих границ. Для исключения пересечений границы интервалов задают с точностью, например,
x <= bдля одного участка иx > bдля следующего, чтобы избежать двойного включения точки перехода. - Сортировка интервалов. При работе с набором интервалов желательно отсортировать их по возрастанию начала, что упрощает проверку на пересечения и последующую обработку.
При использовании конструкции if-elseif-else в Matlab важно расположить условия строго по возрастанию интервалов и избегать повторных проверок, которые могут создавать неоднозначность.
- Сначала проверяют самый левый интервал с условием
x <= x1. - Далее идут промежуточные с условиями вида
x > x1 && x <= x2, гдеx1иx2– границы соседних участков. - Завершающий интервал покрывает все оставшиеся значения.
Если интервалы заданы массивами или структурами, для их обработки используют векторизованные функции, которые предварительно фильтруют пересекающиеся диапазоны или объединяют пересекающиеся участки в один.
Итог: контроль пересечений интервалов на этапе задания функции и чёткое разграничение условий предотвращают ошибки и обеспечивают корректное выполнение кусочной функции в Matlab.
Вопрос-ответ:
Как задать кусочную функцию в Matlab с использованием условных операторов?
В Matlab можно определить кусочную функцию с помощью оператора if-elseif-else. Для этого внутри функции или скрипта прописываются условия, которые задают разные выражения для разных областей аргумента. Например, для переменной x: если x меньше нуля, функция возвращает одно значение, если x от 0 до 1 — другое, и так далее. Такой подход позволяет явно управлять значениями функции на различных интервалах.
Какие существуют альтернативные методы задания кусочных функций в Matlab без использования условных операторов?
Кроме if-elseif-else, можно применять логические индексы и векторные операции. Например, создают вектор значений x и для каждого диапазона используют логические маски: x<0, (x>=0)&(x<=1) и т. п. Каждому подмножеству присваивают соответствующее значение, а затем объединяют результаты. Такой способ удобен при работе с большими массивами данных и позволяет избежать циклов и вложенных условий.
Как построить график кусочной функции в Matlab?
Для графика сначала создают вектор аргументов с нужным диапазоном. Затем с помощью условных операторов или логических индексов вычисляют значения функции для каждого элемента вектора. После этого используется команда plot(x, y), где x — вектор аргументов, а y — соответствующие значения функции. Важно, чтобы значения y были рассчитаны для всех точек из x, иначе график получится неполным.
Можно ли задавать кусочные функции в Matlab с помощью встроенной функции piecewise?
Да, начиная с более новых версий Matlab, существует функция piecewise, которая позволяет объявлять кусочные функции компактно. В неё передают пары условий и соответствующих значений, например: piecewise(x<0, 0, x>=0 & x<1, x^2, true, 1). Такой способ упрощает чтение кода и удобен для математических выражений, особенно в символических вычислениях.
Какие ошибки чаще всего возникают при реализации кусочных функций в Matlab и как их избежать?
Типичные ошибки связаны с неверным определением условий, из-за чего некоторые значения аргумента остаются без присвоенного результата, что приводит к появлению NaN. Также можно забыть использовать логические операторы корректно или не учитывать крайние точки интервалов. Для предотвращения этого важно тщательно проверять условия и при необходимости добавлять ветку else для обработки всех оставшихся случаев.
Как в Matlab задать функцию, определённую по частям, без использования цикла?
В Matlab можно использовать конструкцию с логическими выражениями и оператором элементного умножения. Например, если функция имеет два участка: f(x) = x² при x < 0 и f(x) = sqrt(x) при x ≥ 0, то её можно задать так: y = (x.^2).*(x<0) + sqrt(x).*(x≥0). Такой способ позволяет вычислить значение функции для всех элементов массива x сразу, без циклов.
Можно ли в Matlab реализовать кусочную функцию с большим количеством условий и как это лучше сделать?
Да, для задания функций с множеством участков в Matlab удобно применять функцию piecewise, если доступна Symbolic Math Toolbox. Если же этот инструмент не используется, можно комбинировать логические условия с помощью логического сложения и умножения, например: y = f1(x).*(cond1) + f2(x).*(cond2) + … + fn(x).*(condn), где cond1, cond2 и так далее — логические векторы, указывающие области определения каждого участка. Такой способ сохраняет производительность и позволяет быстро менять условия без переписывания циклов.