Реализация нейронной сети без использования высокоуровневых фреймворков, таких как TensorFlow или PyTorch, позволяет точно понять, как работает каждый элемент архитектуры – от прямого распространения до обратного распространения ошибки. Этот подход особенно важен для закрепления теоретических основ и углублённого понимания численных методов, применяемых в машинном обучении.
Python предоставляет широкий набор инструментов для реализации нейронных сетей с нуля. Библиотека NumPy используется для работы с матрицами и векторизацией вычислений, а matplotlib и seaborn помогают визуализировать процесс обучения и распределение ошибок. Благодаря этому можно сконцентрироваться на логике модели без отвлечения на детали интерфейса или автоматизации, скрывающей важные этапы обучения.
Ключевыми шагами в создании сети являются: инициализация весов, определение функции активации (чаще всего sigmoid, ReLU или tanh), реализация прямого и обратного распространения, а также оптимизация градиентного спуска. Без автоматической дифференциации важно вручную вычислить градиенты и убедиться в их корректности через численную проверку (gradient checking).
Такой подход позволяет глубже понять чувствительность сети к выбору гиперпараметров: скорости обучения, архитектуре (количество слоёв и нейронов), а также функции потерь. Это знание критично при разработке собственных решений и при отладке нестандартных моделей, где стандартные фреймворки оказываются избыточными или непрозрачными.
Выбор и настройка среды разработки для Python и NumPy
Для создания нейронных сетей с нуля рекомендуется использовать версию Python не ниже 3.9. Установка осуществляется через официальный сайт python.org. После установки проверьте доступность Python и pip в терминале командой python —version и pip —version.
Для управления зависимостями используйте venv или virtualenv. Создайте виртуальную среду командой python -m venv venv, активируйте её: source venv/bin/activate (Linux/macOS) или venv\Scripts\activate (Windows). Убедитесь, что pip работает внутри виртуальной среды.
NumPy устанавливается через pip: pip install numpy. Убедитесь в корректной установке, запустив Python-интерпретатор и выполнив: import numpy as np; np.__version__. Версия должна быть не ниже 1.23 для обеспечения совместимости с современными библиотеками машинного обучения.
Для разработки подойдёт Visual Studio Code с установленным расширением Python от Microsoft. В настройках выберите интерпретатор из виртуальной среды: Ctrl+Shift+P → Python: Select Interpreter. Альтернатива – PyCharm Community, где путь к интерпретатору задаётся через Settings → Project → Python Interpreter.
Установите расширение Jupyter в VS Code, если планируется работа с ноутбуками. Для запуска используйте команду pip install notebook и запускайте через jupyter notebook в корне проекта.
Для ускорения линейных операций установите MKL-сборку NumPy, если используется CPU от Intel: pip install numpy -i https://pypi.anaconda.org/intel/simple. Это даст прирост производительности до 10x при больших объемах данных.
Рекомендуется создать файл requirements.txt с зависимостями: numpy>=1.23, что обеспечит воспроизводимость среды при развёртывании или переносе проекта.
Инициализация весов и смещений без использования библиотек машинного обучения

Корректная инициализация весов и смещений – ключ к стабильному обучению нейронной сети. При реализации с нуля на Python важно вручную задать начальные значения, избегая проблем затухающего или взрывающегося градиента.
- Для весов слоя предпочтительно использовать равномерное или нормальное распределение, масштабированное в зависимости от количества входов.
- Смещения инициализируются нулями или малыми положительными значениями (например, 0.01), чтобы избежать симметрии в активации нейронов.
Пример инициализации весов и смещений скрытого слоя из 64 нейронов, принимающего 100 входов:
import random
import math
input_size = 100
hidden_size = 64
weights = [[random.uniform(-1, 1) * math.sqrt(2 / input_size) for _ in range(input_size)] for _ in range(hidden_size)]
biases = [0.01 for _ in range(hidden_size)]
Альтернативный подход – использовать нормальное распределение:
weights = [[random.gauss(0, math.sqrt(2 / input_size)) for _ in range(input_size)] for _ in range(hidden_size)]
Рекомендации:
- Используй
math.sqrt(2 / n)при ReLU-активации (инициализация Хе). - Для сигмоидной или tanh-активации –
math.sqrt(1 / n)(инициализация Ксавье). - Не инициализируй все веса одинаковыми значениями – это остановит обучение.
- Инициализируй веса каждого слоя отдельно, учитывая количество входов в него.
Такая инициализация улучшает сходимость сети и делает обучение более стабильным.
Реализация функции активации ReLU и её производной вручную
Функция активации ReLU (Rectified Linear Unit) задаётся формулой f(x) = max(0, x). Эта функция обнуляет все отрицательные значения входного тензора, пропуская положительные без изменений. Она не только снижает вероятность возникновения градиентного затухания, но и требует минимальных вычислительных затрат.
Для её реализации вручную в чистом Python без использования библиотек типа NumPy достаточно пройтись по каждому элементу входного списка:
def relu(x):
return [max(0, i) for i in x]Если вход – скаляр, обрабатываем отдельно:
def relu_scalar(x):
return max(0, x)Производная ReLU равна 1 при x > 0 и 0 при x ≤ 0. При ручной реализации важно обеспечить соответствие этим условиям для каждого элемента входа:
def relu_derivative(x):
return [1 if i > 0 else 0 for i in x]Для скалярного аргумента:
def relu_derivative_scalar(x):
return 1 if x > 0 else 0Если требуется работать с вложенными структурами (матрицами), применяйте функцию рекурсивно или используйте вложенные циклы. Пример с двумерным списком:
def relu_matrix(matrix):
return [[max(0, val) for val in row] for row in matrix]
def relu_derivative_matrix(matrix):
return [[1 if val > 0 else 0 for val in row] for row in matrix]Построение прямого распространения сигнала в многослойной сети
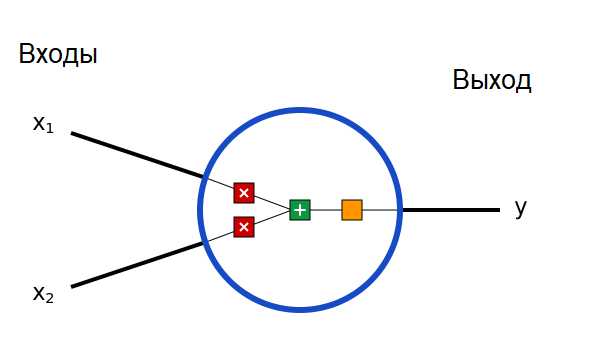
Процесс начинается с подачи входных данных в первый слой. Каждый нейрон на этом слое получает взвешенное значение входных данных и передает его на следующий слой. Веса связаны с важностью соответствующего входа для нейрона. Далее происходит активация, которая вычисляется как функция от суммы входных данных, взвешенных с учетом весов. Распространенные функции активации включают сигмоиду, ReLU и tanh. Выбор функции активации влияет на скорость обучения и конечную точность сети.
Каждое скрытое звено сети вычисляется аналогично: на выходе нейрона будет результат активации, который поступает на следующий слой. Важно помнить, что веса и смещения инициализируются случайным образом в начале обучения, и во время прямого распространения они не изменяются. Активации нейронов в каждом слое становятся входами для следующего слоя.
После прохождения сигнала через все скрытые слои, выходной слой производит итоговый результат. Для задач регрессии на выходе используется линейная активация, для задач классификации – обычно softmax, который преобразует значения в вероятности принадлежности к разным классам.
Алгоритм прямого распространения легко реализуется на Python с использованием библиотеки NumPy. Для этого достаточно выполнить поочередные матричные умножения между входами, весами и добавлением смещений, а затем применить функцию активации. Следующий пример демонстрирует построение простого прямого распространения для сети с одним скрытым слоем:
pythonEditimport numpy as np
# Инициализация весов и смещений
input_size = 3
hidden_size = 4
output_size = 1
W1 = np.random.randn(input_size, hidden_size)
b1 = np.zeros((1, hidden_size))
W2 = np.random.randn(hidden_size, output_size)
b2 = np.zeros((1, output_size))
# Функция активации ReLU
def relu(x):
return np.maximum(0, x)
# Прямое распространение
def forward_propagation(X):
z1 = np.dot(X, W1) + b1
a1 = relu(z1)
z2 = np.dot(a1, W2) + b2
return z2 # Результат для регрессии, для классификации может быть использован softmax
В данном примере прямое распространение включает два слоя: первый скрытый и выходной. Важно правильно настроить размерности матриц, чтобы каждое умножение соответствовало данным. Активация ReLU применяется на скрытом слое, а для задачи регрессии на выходном слое используется линейная функция. Если задача – классификация, то можно заменить выходную активацию на softmax.
Для повышения производительности и избежания проблем, связанных с исчезающим градиентом, часто используется нормализация данных и более сложные функции активации. Такие подходы значительно ускоряют процесс обучения и делают сеть более устойчивой к различным типам данных.
Расчёт градиентов методом обратного распространения ошибки
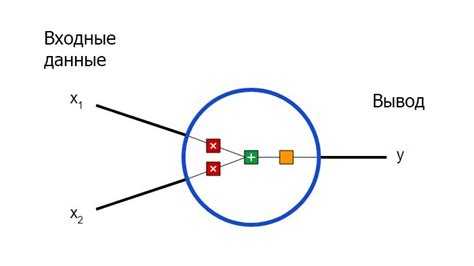
Метод обратного распространения ошибки (backpropagation) используется для вычисления градиентов и обновления весов нейронной сети. Он основан на цепном правиле дифференцирования и позволяет эффективно минимизировать функцию потерь. Для этого происходит два этапа: прямой и обратный проходы.
Прямой проход заключается в вычислении активаций каждого слоя сети. Входные данные проходят через слои с применением линейных преобразований и функций активации, пока не достигают выходного слоя, где вычисляется ошибка. Ошибка сети – это разница между предсказанными и реальными значениями.
На обратном проходе градиенты ошибки передаются от выходного слоя к входному. Для каждого веса сети вычисляется частная производная ошибки по этому весу. Для слоя \(l\) градиент ошибки по весу \(w_{ij}^{(l)}\) может быть вычислен через производную функции потерь по выходу нейрона \(a_j^{(l)}\), произведенную на производную функции активации и производную выхода по весу:
\[
\frac{\partial E}{\partial w_{ij}^{(l)}} = \frac{\partial E}{\partial a_j^{(l)}} \cdot \frac{\partial a_j^{(l)}}{\partial z_j^{(l)}} \cdot \frac{\partial z_j^{(l)}}{\partial w_{ij}^{(l)}}
\]
Здесь:
— \(\frac{\partial E}{\partial a_j^{(l)}}\) – ошибка, переданная с предыдущего слоя;
— \(\frac{\partial a_j^{(l)}}{\partial z_j^{(l)}}\) – производная функции активации для нейрона \(j\) на слое \(l\);
— \(\frac{\partial z_j^{(l)}}{\partial w_{ij}^{(l)}}\) – производная линейного преобразования на слое \(l\) по весу \(w_{ij}\).
Для каждого слоя эта формула повторяется, и на каждом шаге обновляется вес. Градиенты ошибки распространяются от выхода к входу, что позволяет скорректировать веса на каждом уровне. Этот процесс продолжается, пока все веса не будут обновлены.
Важным моментом является выбор алгоритма оптимизации для обновления весов. Наиболее часто используется градиентный спуск, но для улучшения сходимости и скорости обучения применяются адаптивные методы, такие как Adam или RMSProp. Эти алгоритмы автоматически регулируют скорость обучения, что помогает избежать проблем с выбором оптимального шага для градиентного спуска.
Для эффективного расчёта градиентов важно учитывать правильную инициализацию весов и выбор функции активации. Например, использование ReLU вместо сигмоида помогает избежать проблемы исчезающего градиента, особенно в глубоких сетях.
Обновление параметров сети с использованием градиентного спуска

Для обновления параметров нейронной сети используется алгоритм градиентного спуска. Этот метод минимизирует функцию потерь, направляя параметры модели в сторону уменьшения ошибки. Градиентный спуск базируется на вычислении градиента функции потерь по отношению к параметрам и корректировке этих параметров в обратном направлении.
Обновление параметров осуществляется с помощью следующего уравнения:
θ = θ - α * ∇J(θ)
где:
- θ – вектор параметров модели (веса и смещения),
- α – скорость обучения (learning rate), определяет шаг изменения параметров на каждой итерации,
- ∇J(θ) – градиент функции потерь J(θ) по отношению к параметрам.
Градиент указывает на направление, в котором функция потерь увеличивается. Следовательно, мы корректируем параметры в направлении противоположном градиенту, чтобы минимизировать ошибку. Важно правильно подобрать скорость обучения. Если она слишком велика, процесс может стать нестабильным, если слишком мала – сходимость будет слишком медленной.
Существует несколько вариантов градиентного спуска:
- Стандартный градиентный спуск (Batch Gradient Descent) – обновление параметров после обработки всей обучающей выборки. Этот метод точен, но может быть вычислительно затратным для больших данных.
- Стохастический градиентный спуск (Stochastic Gradient Descent, SGD) – обновление параметров после каждой обучающей пары. Метод быстрее, но результат может быть более шумным.
- Мини-батч градиентный спуск (Mini-batch Gradient Descent) – обновление параметров после обработки случайной подвыборки данных. Это компромисс между точностью и вычислительной эффективностью.
Чтобы ускорить процесс обучения, часто применяют различные оптимизаторы, такие как Adam, который использует адаптивные моменты первого и второго порядка, ускоряя сходимость.
Применяя градиентный спуск, важно следить за величиной шага обновления. Также стоит учитывать, что слишком большие параметры могут привести к переобучению, а слишком маленькие – не позволят достичь нужной точности. Регуляризация и использование техник, таких как ранняя остановка, могут помочь избежать этих проблем.
Обработка входных данных: нормализация и формирование батчей
Для успешного обучения нейронной сети важно корректно обрабатывать входные данные. Два ключевых этапа в этом процессе – нормализация и формирование батчей. Каждый из них решает определённые задачи, влияя на эффективность обучения и точность модели.
Нормализация данных
Нормализация данных необходима для того, чтобы модель могла эффективно обучаться, не сталкиваясь с проблемами из-за различий в масштабе признаков. Это особенно важно для алгоритмов, чувствительных к масштабам входных данных, таких как градиентный спуск. Существует несколько методов нормализации, которые часто применяются:
- Мин-макс нормализация: Преобразует значения признаков в диапазон [0, 1]. Для этого используется формула:
X' = (X - X_{min}) / (X_{max} - X_{min}) - Стандартизация: Преобразует данные так, чтобы они имели среднее значение 0 и стандартное отклонение 1. Формула:
X' = (X - μ) / σ, где μ – среднее значение, σ – стандартное отклонение. - Нормализация по Z-оценке: Эта методика также основана на стандартизации, но применяется для более сложных данных, где требуется учитывать различия в разбросе признаков.
Для большинства нейронных сетей стандартными являются мин-макс нормализация или стандартизация. Они позволяют ускорить обучение и улучшить сходимость модели.
Формирование батчей
Обучение нейронных сетей обычно происходит не с использованием всего набора данных сразу, а через использование небольших подмножеств, называемых батчами. Такой подход имеет несколько преимуществ:
- Экономия памяти: Работа с полным набором данных может требовать слишком большого объёма памяти. Батчи позволяют ограничить количество данных, загружаемых в память за один раз.
- Снижение времени обучения: Разбиение на батчи позволяет обновлять веса модели после обработки каждого батча, ускоряя процесс обучения по сравнению с обработкой всех данных сразу.
- Устойчивость к переобучению: Малые батчи могут действовать как форма регуляризации, предотвращая переобучение.
Размер батча является важным гиперпараметром. Он влияет на скорость сходимости и стабильность модели. Рекомендации:
- Малые батчи (например, 32 или 64 примера) могут обеспечивать лучшее общее качество модели, поскольку они часто вводят шум в процесс оптимизации, предотвращая переобучение.
- Большие батчи (например, 128 или 256) могут ускорить обучение, но увеличивают риск переобучения и требуют больше памяти.
- Зависимость от объёма данных: Для небольших наборов данных лучше использовать меньшие батчи, тогда как для больших наборов данных размер батча может быть увеличен для ускорения вычислений.
Практическая реализация в Python
Для нормализации и формирования батчей часто используются библиотеки, такие как NumPy и TensorFlow или PyTorch. В этих фреймворках есть встроенные методы, которые упрощают процесс:
- TensorFlow: Для нормализации можно использовать
tf.keras.layers.Normalization, а для батчей –tf.data.Dataset.batch(). - PyTorch: Нормализация может быть реализована через
torchvision.transforms.Normalize(), а батчи формируются с помощьюtorch.utils.data.DataLoader.
Вручную нормализовать данные можно, например, с помощью scikit-learn, используя MinMaxScaler или StandardScaler для стандартизации. Батчи могут быть сформированы с помощью функции numpy.array_split() или torch.utils.data.DataLoader.
Важно помнить, что нормализация должна проводиться на обучающих данных, а затем те же преобразования должны быть применены к тестовым данным, чтобы сохранить совместимость распределений.
Тестирование обученной нейросети на простом наборе данных
Предположим, что нейросеть была обучена для классификации изображений. Тестирование на MNIST начинается с загрузки тестовой выборки, которая включает 10 тысяч изображений цифр. Разделение данных на обучающую и тестовую выборки уже сделано на этапе подготовки данных, так что можно сразу перейти к обработке тестового набора.
Для оценки работы нейросети на тестовых данных чаще всего используют метрики точности (accuracy), которые измеряют, насколько правильно модель классифицирует изображения. Для вычисления точности необходимо пройти по всем тестовым примерам, выполнить предсказания и сравнить их с реальными метками.
Пример кода для тестирования нейросети на наборе данных MNIST в Python:
import tensorflow as tf
from tensorflow.keras import datasets, models
# Загрузка данных
(train_images, train_labels), (test_images, test_labels) = datasets.mnist.load_data()
# Нормализация данных
test_images = test_images / 255.0
# Создание и загрузка модели
model = models.load_model('trained_model.h5')
# Оценка точности
test_loss, test_acc = model.evaluate(test_images, test_labels, verbose=2)
print(f'Точность на тестовом наборе: {test_acc}')
В этом примере модель загружается из файла ‘trained_model.h5’, и производится её оценка на тестовом наборе. Функция evaluate() возвращает два значения: потери (loss) и точность (accuracy). Чем выше точность, тем лучше модель справляется с задачей.
В случае, если точность на тестовых данных значительно ниже, чем на обучающих, это может свидетельствовать о переобучении. Для борьбы с этим можно попробовать уменьшить сложность модели, увеличить объём обучающих данных или применить методы регуляризации.
Тестирование на простых наборах данных – это не только проверка точности модели, но и возможность понять, какие улучшения могут быть сделаны для повышения её производительности в реальных условиях.
Вопрос-ответ:
Что нужно знать, чтобы создать нейронную сеть на Python с нуля?
Для создания нейронной сети на Python важно разобраться в базовых концепциях машинного обучения, таких как обучающие выборки, функции активации, градиентный спуск и типы нейронных сетей. Также необходимо освоить библиотеки, такие как NumPy для работы с массивами данных и TensorFlow или PyTorch для построения и тренировки моделей. Знания в области линейной алгебры и статистики помогут лучше понять внутренние процессы, происходящие в нейронных сетях.
Как устроены нейронные сети и как они обучаются?
Нейронные сети состоят из слоёв нейронов, которые обрабатывают данные и передают их на следующий слой. Каждый нейрон выполняет математическую операцию, принимая на вход данные, умножая их на веса, добавляя смещение и применяя функцию активации. Обучение нейронной сети происходит через корректировку весов с помощью алгоритма обратного распространения ошибки, который минимизирует разницу между предсказанным и реальным значением с использованием градиентного спуска.
Какие библиотеки для Python лучше всего подходят для создания нейронных сетей?
Для создания нейронных сетей на Python широко используются TensorFlow и PyTorch. TensorFlow предлагает мощные инструменты для разработки, масштабирования и развертывания моделей, а также поддерживает работу на различных устройствах. PyTorch предпочитают за удобство и гибкость, а также за сильную интеграцию с Python, что делает его идеальным для исследований и экспериментов. Также существует Keras, которая является высокоуровневым интерфейсом для работы с TensorFlow.
Какие основные проблемы могут возникнуть при создании нейронных сетей?
При создании нейронных сетей могут возникнуть различные проблемы. Одна из самых распространённых — переобучение модели, когда нейронная сеть слишком точно подстраивается под обучающие данные, теряя способность обобщать на новые данные. Также важно правильно настроить гиперпараметры, такие как скорость обучения, размер мини-батча, количество слоёв и нейронов. Кроме того, может быть сложно собрать достаточное количество качественных данных для обучения модели.
Как можно улучшить точность нейронной сети?
Для повышения точности нейронной сети можно использовать несколько подходов. Во-первых, можно увеличить объём данных для обучения, применяя методы аугментации данных. Во-вторых, стоит экспериментировать с архитектурой сети, добавляя дополнительные слои или изменяя функции активации. Также полезно использовать техники регуляризации, такие как dropout или L2-регуляризация, чтобы предотвратить переобучение. Кроме того, важно тщательно настроить гиперпараметры и попробовать различные алгоритмы оптимизации для достижения лучшего результата.
Как начать создание нейронных сетей с нуля на Python?
Для начала создания нейронных сетей на Python важно изучить основные принципы работы нейронных сетей и математические концепции, такие как линейная алгебра, теория вероятностей и оптимизация. Начать можно с использования библиотек, таких как NumPy для работы с матрицами и TensorFlow или PyTorch для построения и обучения сетей. Первоначально стоит пройти через простые примеры, например, создание перцептрона, а затем постепенно переходить к более сложным моделям, таким как сверточные и рекуррентные нейронные сети. Необходимо также понимать принципы настройки гиперпараметров и алгоритмов оптимизации, таких как градиентный спуск, чтобы успешно обучить модель.