Поворот матрицы на 90 градусов – частая задача в обработке данных, компьютерном зрении и алгоритмах машинного обучения. В Python решение этой задачи можно реализовать несколькими способами, и каждый из них имеет свои преимущества в зависимости от условий задачи. Например, при работе с небольшими матрицами можно использовать простые способы с явными циклами, в то время как для больших матриц стоит рассматривать более оптимизированные методы, например, с использованием библиотек NumPy.
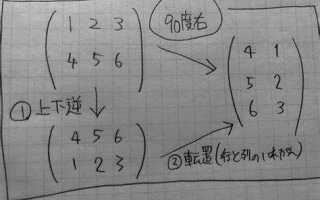
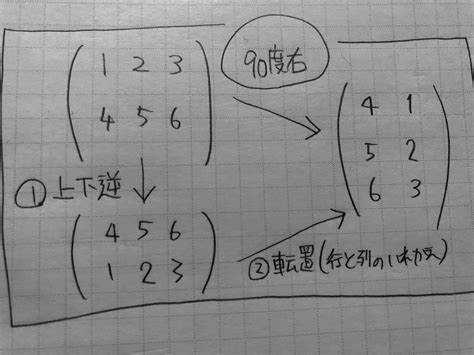
Один из наиболее эффективных способов поворота матрицы на 90 градусов – использование метода с транспонированием и инвертированием строк. Сначала матрица транспонируется, что означает замену строк на столбцы, а затем производится инвертирование строк, чтобы получить поворот на 90 градусов по часовой стрелке. Такой метод работает за время O(n^2), что вполне эффективно для большинства задач.
В случае работы с библиотеками, такими как NumPy, процесс можно значительно упростить. Встроенная функция numpy.rot90() позволяет повернуть матрицу на 90 градусов за один вызов, что делает код более компактным и читаемым. Этот подход также использует оптимизированные алгоритмы для работы с массивами, что важно при работе с большими объемами данных.
Однако, важно учитывать, что выбор метода зависит от контекста: для небольших задач с матрицами в стандартных типах данных Python использование явных циклов может быть вполне достаточным. В случаях, когда важна скорость обработки данных, стоит обратить внимание на библиотеки, такие как NumPy, которые предлагают более быстрые и экономные по времени решения для работы с многомерными массивами.
Создание матрицы в Python с использованием списка списков
Матрица в Python часто представлена как список, содержащий другие списки. Каждый внутренний список представляет собой строку матрицы. Например, чтобы создать матрицу 3×3, можно использовать следующую конструкцию:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
Здесь matrix – это список, содержащий три других списка, каждый из которых представляет строку матрицы. Индексы элементов матрицы можно использовать для доступа к отдельным значениям. Например, чтобы получить элемент из второй строки и третьего столбца, используем выражение matrix[1][2], что вернёт значение 6.
Для создания матрицы произвольных размеров можно использовать вложенные циклы. Например, чтобы создать матрицу размером m x n с начальными значениями, можно воспользоваться таким кодом:
m, n = 3, 4 # размеры матрицы matrix = [[0 for _ in range(n)] for _ in range(m)]
Этот код создаст матрицу 3×4, заполненную нулями. Внешний цикл проходит по строкам, а внутренний – по столбцам. Такая конструкция помогает быстро заполнять матрицу любыми значениями.
Важно помнить, что Python использует динамическую типизацию, и вы можете создать матрицу, где элементы будут иметь разные типы данных. Например, в одной строке могут быть как числа, так и строки или логические значения:
matrix = [[1, 'a', True], [3.14, 'b', False]]
Однако для математических операций или преобразований, например, поворота матрицы, важно, чтобы элементы были однородными по типу, например, числами. В противном случае могут возникнуть ошибки при обработке данных.
Как понять, что матрица квадратная для поворота на 90 градусов

Проверка, что матрица квадратная, заключается в сравнении этих двух значений. Если они равны, значит, матрица квадратная и ее можно повернуть на 90 градусов. В Python это можно легко проверить с помощью оператора сравнения:
if len(matrix) == len(matrix[0]):
print("Матрица квадратная")
else:
print("Матрица не квадратная")
При этом важно помнить, что в случае неквадратной матрицы поворот на 90 градусов может быть невозможен или приведет к потере данных. Например, матрица с размерами 3×2 не может быть повернута в привычном смысле без изменения ее структуры.
Таким образом, для поворота матрицы на 90 градусов важно, чтобы она была квадратной. Проверка этого условия не требует сложных вычислений и занимает минимальное время, что делает этот процесс быстрым и эффективным.
Использование встроенных функций Python для переворота матрицы

В Python для переворота матрицы на 90 градусов можно эффективно использовать встроенные функции и методы. Рассмотрим несколько подходов, которые позволят решить эту задачу с использованием стандартных возможностей языка.
Одним из самых удобных способов является использование функции zip в сочетании с распаковкой аргументов. Это позволяет транспонировать матрицу и затем инвертировать строки, что эквивалентно повороту на 90 градусов.
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
rotated_matrix = [list(row) for row in zip(*matrix[::-1])]
В этом примере сначала используется matrix[::-1], чтобы инвертировать строки матрицы. Затем применяется zip(*matrix) для транспонирования полученной матрицы. Результат – повёрнутая на 90 градусов матрица.
Еще одним полезным инструментом является библиотека numpy, которая предоставляет функцию rot90 для удобного поворота матриц.
import numpy as np
matrix = np.array([
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
])
rotated_matrix = np.rot90(matrix)
Использование numpy.rot90() минимизирует количество кода и делает решение задачи более лаконичным, особенно при работе с большими матрицами.
Если же задача заключается в манипуляции с данными без использования внешних библиотек, можно воспользоваться стандартными списковыми методами Python. Например, создать новую матрицу, добавляя в неё элементы в нужном порядке.
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
rotated_matrix = []
for i in range(len(matrix[0])):
rotated_matrix.append([row[i] for row in matrix[::-1]])
Этот код выполняет поворот матрицы на 90 градусов путём транспонирования и инвертирования строк вручную. Хотя это менее эффективно, чем использование numpy, такой способ подойдет для небольших матриц и случаев, когда необходимо ограничиться стандартными средствами Python.
Для улучшения производительности и сокращения времени выполнения в случае с большими матрицами предпочтительнее использовать библиотеку numpy, так как её функции оптимизированы для работы с многомерными массивами и позволяют быстро и эффективно выполнять операции поворота.
Алгоритм поворота матрицы с использованием индексов
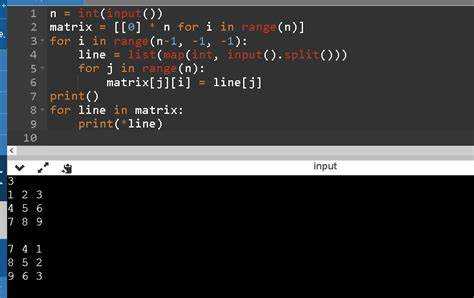
Поворот матрицы на 90 градусов по часовой стрелке можно выполнить с помощью изменения индексов её элементов. Рассмотрим алгоритм, который работает на основе транспонирования матрицы и её отражения.
Предположим, что у нас есть квадратная матрица размера n x n. Для поворота на 90 градусов по часовой стрелке, выполните следующие шаги:
- Транспонируйте матрицу. Это значит, что элементы на позициях
matrix[i][j]иmatrix[j][i]меняются местами для всехiиj. - Отразите транспонированную матрицу по вертикали, т.е. поменяйте местами элементы
matrix[i][j]иmatrix[i][n-1-j]для всехiиj.
Это решение работает за время O(n²), так как каждая операция (транспонирование и отражение) требует O(n²) шагов.
Пример кода на Python:
def rotate_matrix(matrix): n = len(matrix) # Транспонирование матрицы for i in range(n): for j in range(i + 1, n): matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j] # Отражение по вертикали for i in range(n): for j in range(n // 2): matrix[i][j], matrix[i][n - 1 - j] = matrix[i][n - 1 - j], matrix[i][j] return matrix
Таким образом, с помощью этих двух операций можно эффективно повернуть матрицу на 90 градусов. Важно отметить, что этот метод работает только для квадратных матриц. Если вам нужно повернуть прямоугольную матрицу, следует рассматривать другой подход или преобразование её в квадратную форму перед поворотом.
Пример поворота матрицы с помощью библиотеки NumPy

Библиотека NumPy предоставляет удобные методы для работы с матрицами, включая их поворот на 90 градусов. Рассмотрим простой способ выполнения этой операции с помощью функции numpy.rot90.
Основной функцией для поворота матрицы является numpy.rot90. Она принимает два аргумента: саму матрицу и количество поворотов на 90 градусов по часовой стрелке. По умолчанию матрица поворачивается на 90 градусов.
Пример:
import numpy as np
matrix = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
rotated_matrix = np.rot90(matrix)
print(rotated_matrix)
Этот код создаёт матрицу 3×3 и поворачивает её на 90 градусов. Результат будет следующим:
[[3 6 9]
[2 5 8]
[1 4 7]]
Функция numpy.rot90 также позволяет указать количество поворотов. Например, чтобы повернуть матрицу на 180 градусов, нужно вызвать функцию дважды:
rotated_matrix_180 = np.rot90(matrix, 2)
print(rotated_matrix_180)
Этот код вернёт матрицу, повернутую на 180 градусов:
[[9 8 7]
[6 5 4]
[3 2 1]]
Для поворота на 270 градусов достаточно передать в функцию значение 3:
rotated_matrix_270 = np.rot90(matrix, 3)
print(rotated_matrix_270)
Результат будет следующим:
[[7 4 1]
[8 5 2]
[9 6 3]]
Таким образом, функция numpy.rot90 предоставляет простой способ для поворота матриц на 90, 180 и 270 градусов. Вы можете использовать её для решения задач, связанных с манипуляцией и трансформацией данных в Python.
Сравнение производительности различных способов поворота матрицы
Существует несколько подходов для поворота матрицы на 90 градусов. Каждый из них имеет свои особенности, которые влияют на производительность в зависимости от размера матрицы и требований к памяти.
Первый способ – это использование дополнительной матрицы. Для этого создаётся новая матрица той же размерности, в которую поочередно копируются элементы из исходной матрицы с учётом их нового расположения. Этот метод прост в реализации, но имеет большую временную и пространственную сложность. Его время выполнения составляет O(n^2), где n – размер стороны квадратной матрицы. Это решение требует также O(n^2) памяти для хранения новой матрицы.
Второй способ – поворот матрицы на месте. Он оптимизирует использование памяти, так как не требует выделения дополнительной памяти для нового массива. Алгоритм состоит из последовательных обменов элементов в матрице. Это решение также имеет временную сложность O(n^2), но требует O(1) дополнительной памяти. Однако оно немного сложнее для реализации из-за необходимости аккуратно обменивать элементы в процессе выполнения.
Третий способ – использование библиотеки NumPy. Встроенные функции этой библиотеки часто оптимизированы для быстрого выполнения операций с многомерными массивами. Время работы стандартных методов NumPy зависит от реализации, но в среднем они могут быть быстрее на больших матрицах по сравнению с чисто Python-решениями. Однако при этом память может использоваться не так эффективно, как в случае поворота на месте.
Если матрица имеет большой размер (например, несколько тысяч строк и столбцов), то NumPy может показать заметное преимущество в скорости из-за низкоуровневой оптимизации операций. Для небольших матриц различия в производительности будут незначительными, и поворот на месте может быть предпочтительнее, так как он минимизирует использование памяти.
Выбор метода зависит от задач. Если важна минимизация использования памяти и матрица небольшая, лучше выбрать метод поворота на месте. Для более крупных данных или в случае необходимости быстрого выполнения на больших объёмах данных стоит рассматривать использование библиотеки NumPy.
Ошибки и проблемы при повороте матрицы в Python
Еще одна сложность – это необходимость изменять ориентацию матрицы в месте. Если работать с неизменяемыми структурами данных, такими как кортежи, потребуется создать новую матрицу, что увеличивает расход памяти и может замедлить выполнение программы для больших данных. Лучше всего использовать списки, так как они позволяют модифицировать элементы без создания копий данных.
При использовании встроенных функций Python для работы с матрицами (например, с NumPy) может возникнуть путаница в том, что такая операция, как транспонирование или вращение, изменяет исходную матрицу. Чтобы избежать нежелательных побочных эффектов, следует работать с копиями исходных данных, если требуется сохранить исходную структуру.
Нельзя не учитывать размер матрицы. Например, при попытке поворота прямоугольной матрицы на 90 градусов могут возникнуть проблемы с перераспределением элементов, если не правильно пересчитывать новые индексы для строк и столбцов. Важно помнить, что для правильного поворота строки станут столбцами, а столбцы – строками, что меняет структуру данных.
При реализации поворота на 90 градусов вручную важно избежать ошибки, связанной с порядком операций. Для корректного поворота сначала необходимо транспонировать матрицу, а затем инвертировать строки. Прямое вращение матрицы без учета этого порядка может привести к некорректным результатам.
Когда матрица имеет неравномерные размеры (например, пустые строки или столбцы), это может вызвать дополнительные проблемы при обработке данных. В таких случаях рекомендуется сначала нормализовать матрицу, приведя все строки и столбцы к одинаковой длине, чтобы избежать ошибок при трансформации.