Фазовый портрет – это графическое представление всех возможных траекторий системы во всех возможных состояниях. Он помогает наглядно исследовать динамические системы, такие как модели механических процессов, биологических популяций или экономических моделей. Создание фазового портрета позволяет выявить устойчивость системы, ее поведение в различных состояниях и выделить ключевые особенности, такие как пределы, циклические движения или хаотическое поведение.
Для построения фазового портрета в Python часто используется библиотека Matplotlib для визуализации и NumPy для численного решения дифференциальных уравнений, которые описывают динамическую систему. Важно правильно настроить сетку фазового пространства и выбрать подходящие начальные условия, чтобы точно отобразить поведение системы. Математическая модель системы обычно представляется системой дифференциальных уравнений первого порядка, которые могут быть решены методом численного интегрирования.
Для работы с динамическими системами в Python можно применить функцию odeint из библиотеки scipy.integrate, которая позволяет решать системы обыкновенных дифференциальных уравнений. Параметры этой функции обеспечивают необходимую точность, а встроенные методы управления шагом позволяют адаптировать расчет для разных типов динамик. Правильный выбор параметров интегратора напрямую влияет на точность фазового портрета и корректность отображения всех ключевых аспектов системы.
Таким образом, построение фазового портрета – это не просто процесс визуализации, но и важная часть анализа системы, помогающая выявить ее устойчивые и нестабильные состояния, а также предсказать поведение в долгосрочной перспективе. Ключевым моментом является выбор правильных начальных условий и параметров интегратора для точного отображения динамики системы на фазовом портрете.
Подготовка данных для построения фазового портрета
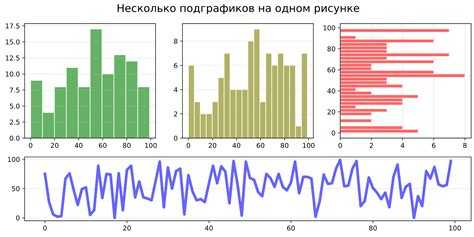
Для построения фазового портрета динамической системы необходимо подготовить данные о ее состоянии в различные моменты времени. Важно учитывать, что фазовый портрет отображает траекторию, описывающую эволюцию системы в фазовом пространстве. Основные шаги подготовки данных включают выбор переменных, их численные значения и временные параметры.
- Выбор переменных – важно выбрать все ключевые переменные, которые определяют состояние системы. Например, для системы с двумя переменными (x и y) необходимо учитывать оба этих параметра, так как каждый из них влияет на динамику системы.
- Моделирование системы – необходимо решить систему дифференциальных уравнений, описывающих динамику системы. Для этого используются численные методы интегрирования, такие как метод Эйлера или Рунге-Кутты. Важно выбрать подходящий метод в зависимости от требуемой точности и типа системы.
- Настройка начальных условий – выбор начальных значений для каждой из переменных имеет большое значение, так как фазовый портрет может существенно изменяться при различных начальных условиях. Начальные значения должны быть выбраны так, чтобы покрыть интересующую область фазового пространства.
- Интервал времени – для получения качественного фазового портрета нужно выбрать соответствующий интервал времени, в котором система будет наблюдаться. Этот интервал должен быть достаточно большим, чтобы система успела достичь устойчивого поведения, но не слишком большим, чтобы избежать ненужных вычислений.
- Шаг интегрирования – для точного расчета траектории важно выбрать подходящий шаг интегрирования. Чем меньше шаг, тем точнее будет результат, однако это увеличивает вычислительные затраты. Рекомендуется начинать с небольшого шага и проверять стабильность решения.
На основе полученных данных можно построить фазовый портрет, который будет наглядно отображать поведение системы. Важно понимать, что подготовка данных включает не только вычисления, но и анализ полученных результатов для корректной интерпретации фазового портрета.
Выбор библиотеки для моделирования динамических систем

Для моделирования динамических систем в Python существует несколько эффективных библиотек, каждая из которых имеет свои особенности и области применения. Рассмотрим наиболее популярные из них.
NumPy является основной библиотекой для работы с числовыми массивами и линейной алгеброй. Он обеспечивает быстрые вычисления, что важно при решении дифференциальных уравнений, использующих большие массивы данных. Однако, NumPy не предоставляет специализированных инструментов для моделирования динамических систем, таких как интеграторы или функции для построения фазовых портретов.
SciPy расширяет возможности NumPy, предоставляя функции для численного решения дифференциальных уравнений (например, odeint). Это делает SciPy одним из лучших выборов для моделирования динамических систем. SciPy также включает инструменты для оптимизации, интерполяции и статистики, что может быть полезно при анализе полученных данных. Одна из сильных сторон SciPy – наличие множества интеграторов с разными свойствами (например, адаптивные шаги для улучшения точности).
Matplotlib идеально подходит для визуализации фазовых портретов и других графиков, необходимых для анализа динамических систем. Он предоставляет мощные функции для построения графиков и диаграмм, включая возможность кастомизации. Хотя Matplotlib не включает в себя алгоритмы моделирования, его тесная интеграция с NumPy и SciPy делает его незаменимым инструментом для визуализации результатов моделирования.
PyDSTool – специализированная библиотека для моделирования и анализа динамических систем, которая включает средства для работы с дифференциальными и алгебраическими уравнениями. Она поддерживает как численные, так и символические методы решения уравнений. PyDSTool обладает большим функционалом для построения фазовых портретов и анализа устойчивости системы.
SymPy является библиотекой для символьных вычислений, и, хотя она не предназначена напрямую для численного моделирования, может быть полезна при исследовании аналитических решений динамических систем и их фазовых портретов. Символьная математика позволяет выявлять общие закономерности в уравнениях, а также проверять устойчивость решений, что может дополнить численные методы.
PyPlot в контексте моделирования динамических систем представляет собой средство для быстрого создания 2D и 3D графиков. Это более специализированный инструмент для визуализации, чем Matplotlib, но иногда его возможности могут быть полезны при быстром тестировании и создании иллюстраций для фазовых портретов.
Если требуется более сложное моделирование с учётом стокастических эффектов, то можно обратить внимание на StochPy или PySCeS. Эти библиотеки предоставляют средства для работы с нелинейными динамическими системами, где нужно учитывать случайные флуктуации и шум.
В зависимости от цели, комбинирование нескольких библиотек часто является наилучшим решением. Например, SciPy для численного моделирования и Matplotlib для визуализации – это стандартное решение для многих задач. Для более сложных и специализированных систем стоит использовать PyDSTool или другие библиотеки, заточенные под динамические системы.
Решение системы дифференциальных уравнений с использованием scipy
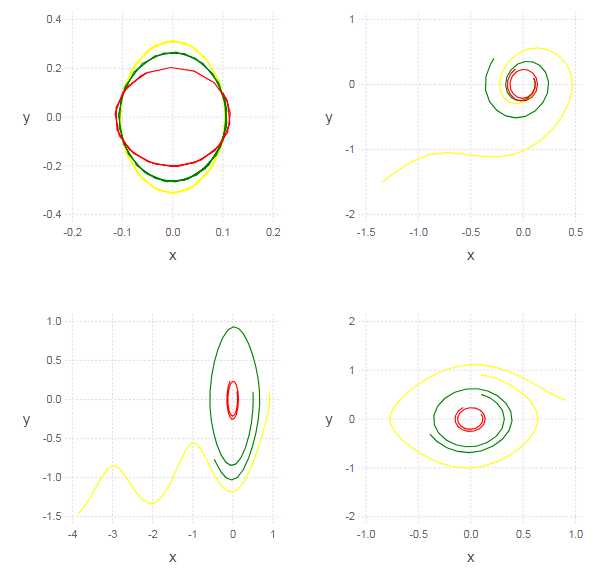
Для решения системы дифференциальных уравнений в Python часто используют библиотеку scipy.integrate, которая предоставляет удобные функции для численного интегрирования, такие как odeint и solve_ivp. Рассмотрим, как применить эти инструменты для решения системы обыкновенных дифференциальных уравнений (ОДУ).
Предположим, что у нас есть система двух уравнений первого порядка:
dx/dt = f(x, y)
dy/dt = g(x, y)
Задача состоит в том, чтобы численно решить эту систему для заданных начальных условий. Рассмотрим использование функции solve_ivp для этого.
Пример кода:
from scipy.integrate import solve_ivp
import numpy as np
import matplotlib.pyplot as plt
# Определим систему уравнений
def system(t, z):
x, y = z
dxdt = x - y
dydt = x + y
return [dxdt, dydt]
# Начальные условия
z0 = [1, 0]
# Временной интервал
t_span = (0, 10)
t_eval = np.linspace(0, 10, 100)
# Решение системы
sol = solve_ivp(system, t_span, z0, t_eval=t_eval)
# График решения
plt.plot(sol.t, sol.y[0], label='x(t)')
plt.plot(sol.t, sol.y[1], label='y(t)')
plt.legend()
plt.xlabel('t')
plt.ylabel('Solution')
plt.title('Решение системы дифференциальных уравнений')
plt.show()
Здесь solve_ivp решает систему на интервале от 0 до 10 с начальными условиями [1, 0]. Функция system определяет правые части уравнений. Результат сохраняется в объекте sol, который содержит как временные точки sol.t, так и значения решения для каждой из переменных sol.y.
Важно: для более точных результатов и в случае нестандартных задач рекомендуется использовать методы интегрирования с меньшим шагом или изменять параметры, такие как method в функции solve_ivp. Например, для жестких систем стоит использовать метод ‘LSODA’.
Если задача состоит в решении системы векторных уравнений с жесткими условиями, то функция odeint может быть удобной, но в большинстве случаев solve_ivp предлагает больше гибкости и возможностей для настройки.
Построение траекторий на фазовом портрете
Для этого сначала необходимо задать систему уравнений, описывающую динамическую систему. Например, для системы двух переменных (x, y) уравнения могут быть следующими:
dx/dt = f(x, y) dy/dt = g(x, y)
Где f и g – это функции, которые зависят от состояния системы. Эти функции определяют динамику изменения переменных во времени.
Далее, используя библиотеку SciPy, можно интегрировать систему уравнений с помощью функции scipy.integrate.solve_ivp. Она позволяет задать начальные условия, временной интервал и метод численного решения. Важный момент – нужно правильно выбрать интервал времени, чтобы траектория была достаточно точной и информативной для анализа.
Пример кода для построения траектории системы с двумя переменными:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
# Определяем систему уравнений
def system(t, z):
x, y = z
dxdt = x - y
dydt = x + y
return [dxdt, dydt]
# Начальные условия
z0 = [1, 0]
# Время
t_span = (0, 10)
t_eval = np.linspace(0, 10, 500)
# Интеграция
solution = solve_ivp(system, t_span, z0, t_eval=t_eval)
# Построение фазового портрета
plt.plot(solution.y[0], solution.y[1])
plt.xlabel('x')
plt.ylabel('y')
plt.title('Фазовый портрет')
plt.show()
В данном примере система состоит из двух уравнений, описывающих динамику переменных x и y. Результат интеграции отображается в фазовом пространстве как траектория, которая демонстрирует, как изменяются состояния системы во времени.
Для более сложных систем, например, с тремя и более переменными, подход остается аналогичным. Важно помнить, что траектории будут зависеть от начальных условий. Чтобы визуализировать их для различных точек начала, достаточно запустить интеграцию с разными начальными значениями и отобразить все траектории на одном графике.
Визуализация фазовых портретов позволяет оценить стабильность системы, выявить циклические и хаотические поведения, а также понять, как система реагирует на изменения начальных условий. Для динамических систем с нелинейными уравнениями фазовый портрет может представлять собой сложные кривые, пересекающиеся в различных точках или стремящиеся к аттракторам.
Добавление направляющих векторных полей на фазовый портрет
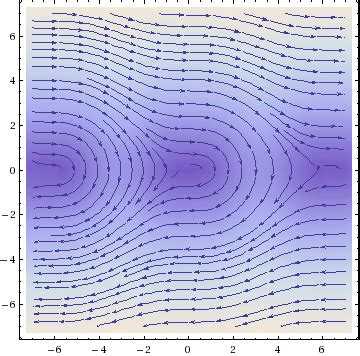
Направляющие векторные поля играют важную роль в анализе динамических систем, визуализируя поведение системы в фазовом пространстве. Эти векторы показывают направление, в котором изменяются состояния системы, и помогают выделить устойчивые и неустойчивые области. Для добавления направляющих векторных полей на фазовый портрет в Python можно использовать библиотеку matplotlib совместно с numpy для вычислений.
Основные этапы:
- Определение системы дифференциальных уравнений.
- Вычисление векторного поля.
- Отображение векторного поля на фазовом портрете.
Рассмотрим простую систему уравнений с двумя переменными, например, систему Лотки-Вольтерры:
dx/dt = αx - βxy dy/dt = δxy - γy
Для вычисления направляющих векторных полей нужно задать функции для производных dx/dt и dy/dt:
def system(x, y, α=1, β=0.1, δ=0.1, γ=1): dxdt = α * x - β * x * y dydt = δ * x * y - γ * y return dxdt, dydt
После того как система определена, можно вычислить значения направляющих векторов для сетки точек в фазовом пространстве. Используем numpy для создания сетки и вычисления производных:
import numpy as np
import matplotlib.pyplot as plt
# Создание сетки
x = np.linspace(0, 10, 20)
y = np.linspace(0, 10, 20)
X, Y = np.meshgrid(x, y)
# Вычисление направляющих векторов
U, V = system(X, Y)
# Построение фазового портрета с векторами
plt.quiver(X, Y, U, V, angles='xy', scale_units='xy', scale=1)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Фазовый портрет с направляющими векторными полями')
plt.show()
В этом примере функция quiver используется для отображения направляющих векторов. Параметры angles='xy' и scale=1 гарантируют, что векторы будут отображаться правильно по отношению к осям.
Чтобы улучшить визуализацию и повысить информативность фазового портрета, можно добавить следующие элементы:
- Управление плотностью сетки: Изменение числа точек сетки позволяет изменять разрешение векторного поля, что может быть полезно для точных вычислений в конкретных областях фазового пространства.
- Цвета и стили: Использование цветовой карты для изменения цвета векторов в зависимости от их величины может дать дополнительные указания на скорость изменения состояния системы.
- Устойчивость и неустойчивость: Для выделения устойчивых и неустойчивых точек можно добавить специальные маркеры или метки, которые будут указывать на фиксированные точки (например, точки равновесия).
Дополнительно можно использовать метод streamplot в matplotlib для более гладкой и детализированной визуализации потоков вектора. Это позволяет лучше видеть структуру фазового портрета, особенно если система имеет сложные траектории.
plt.streamplot(X, Y, U, V, color=np.sqrt(U2 + V2), linewidth=1, cmap='autumn')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Фазовый портрет с потоками')
plt.show()
С помощью этих методов можно детально анализировать динамику системы, выделяя важные особенности, такие как точки равновесия, циклические траектории и поведение в окрестности этих точек.
Анализ устойчивости точек равновесия с помощью фазового портрета

Для анализа устойчивости используются различные методы, включая линейный анализ и исследование характера траекторий. Основные типы устойчивости точек равновесия следующие:
- Устойчивый узел: Траектории, приближающиеся к точке равновесия, ведут систему к ней по спирали.
- Неустойчивый узел: Траектории удаляются от точки равновесия, также по спирали, но в противоположном направлении.
- Циклическая точка (периодическая траектория): Траектории системы образуют замкнутые окружности вокруг точки равновесия.
- Седло: Траектории направляются к точке вдоль некоторых направлений (стабильных), но вдоль других – расходятся (нестабильных).
- Неустойчивый фокус: Траектории сходятся или расходятся с определённым углом к осям, но без резкого скачка.
Простой метод анализа устойчивости точек равновесия – это линейная аппроксимация системы. Для этого нужно вычислить якобиан системы в каждой точке равновесия. Если все собственные значения якобиана имеют отрицательные действительные части, точка равновесия устойчива. Если хотя бы одно собственное значение имеет положительную действительную часть, точка неустойчива.
Для динамических систем можно использовать Python-библиотеки, такие как NumPy для вычисления собственных значений якобиана, и Matplotlib для визуализации фазового портрета. Важно учитывать, что фазовый портрет даёт качественную картину поведения системы, но для точного количественного анализа нужно учитывать и другие методы, например, численное решение дифференциальных уравнений.
Пример построения фазового портрета в Python можно реализовать следующим образом:
import numpy as np
import matplotlib.pyplot as plt
def system(x, y):
dxdt = x - y
dydt = x + y
return np.array([dxdt, dydt])
x_vals = np.linspace(-5, 5, 20)
y_vals = np.linspace(-5, 5, 20)
X, Y = np.meshgrid(x_vals, y_vals)
U, V = system(X, Y)
plt.streamplot(X, Y, U, V, color='r')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Фазовый портрет системы')
plt.show()
Этот код строит фазовый портрет для линейной системы, чьи уравнения описаны выше. Важно заметить, что визуализация фазового портрета и анализ устойчивости точек равновесия должны быть выполнены с учётом конкретных особенностей каждой системы.
Интерактивное исследование фазового портрета с использованием matplotlib
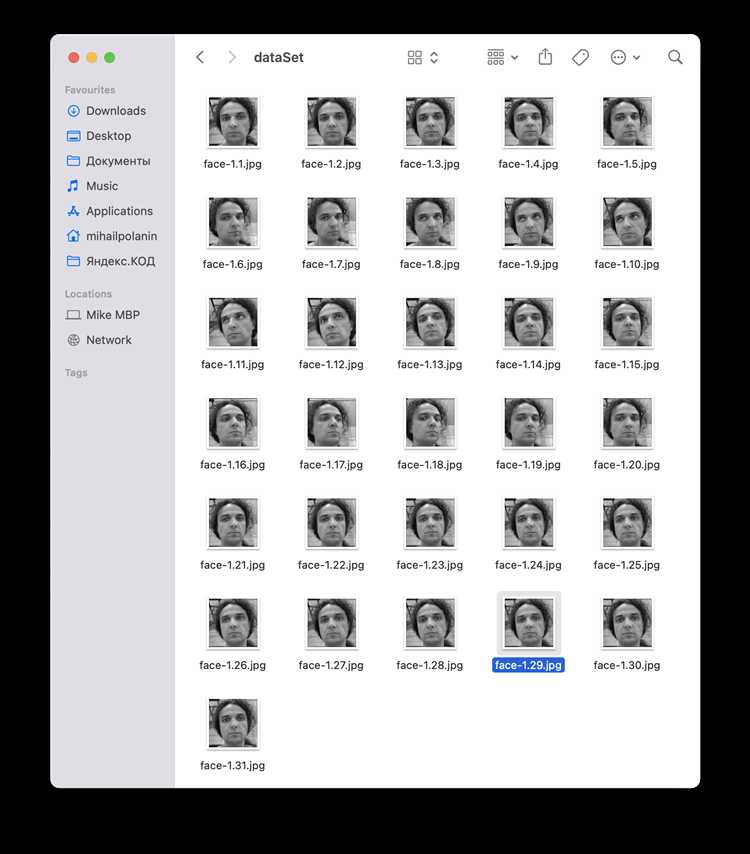
Для построения фазового портрета динамической системы в Python часто используется библиотека matplotlib, которая поддерживает создание графиков и визуализацию данных. Однако, для глубокого анализа системы важна не только статическая визуализация, но и возможность взаимодействовать с графиком для исследования поведения системы при различных начальных условиях.
Для создания интерактивного фазового портрета можно использовать модуль matplotlib.widgets, который предоставляет инструменты для добавления интерактивных элементов на график, таких как ползунки или кнопки. Взаимодействие с этими элементами позволяет пользователю изменять параметры системы и сразу наблюдать изменения на графике.
Пример кода для создания интерактивного фазового портрета двухмерной системы:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.widgets import Slider
# Определяем систему уравнений
def system(t, state):
x, y = state
dxdt = x - y
dydt = x + y
return np.array([dxdt, dydt])
# Функция для построения фазового портрета
def plot_phase_portrait(ax, start_x, start_y):
t = np.linspace(0, 10, 100)
initial_conditions = [start_x, start_y]
solution = np.array([initial_conditions])
for i in range(1, len(t)):
dt = t[i] - t[i-1]
next_state = solution[i-1] + system(t[i-1], solution[i-1]) * dt
solution = np.vstack([solution, next_state])
ax.plot(solution[:, 0], solution[:, 1], label="Trajectories", color='blue')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Фазовый портрет')
# Инициализация графика
fig, ax = plt.subplots()
start_x = 0
start_y = 1
plot_phase_portrait(ax, start_x, start_y)
# Добавляем ползунок для изменения начальных условий
ax_slider_x = plt.axes([0.1, 0.01, 0.65, 0.03])
ax_slider_y = plt.axes([0.1, 0.06, 0.65, 0.03])
slider_x = Slider(ax_slider_x, 'Начальное значение x', -10, 10, valinit=start_x)
slider_y = Slider(ax_slider_y, 'Начальное значение y', -10, 10, valinit=start_y)
# Функция обновления графика
def update(val):
ax.clear()
plot_phase_portrait(ax, slider_x.val, slider_y.val)
plt.draw()
slider_x.on_changed(update)
slider_y.on_changed(update)
plt.show()
В этом примере создаются два ползунка, которые позволяют изменять начальные условия для фазового портрета. Каждый раз, когда значение ползунка меняется, график обновляется, что позволяет увидеть, как меняется траектория системы в зависимости от начальных значений.
Важно отметить, что для более сложных систем можно использовать дополнительные инструменты, такие как matplotlib.animation для создания анимаций, или ipywidgets в сочетании с Jupyter Notebooks для более удобного интерфейса взаимодействия с графиками.
Интерактивные элементы дают возможность наглядно исследовать зависимости фазового портрета от различных параметров системы, таких как начальные условия или параметры самой модели. Это полезно для более глубокого понимания динамики системы и выявления ключевых особенностей поведения системы.
Вопрос-ответ:
Что такое фазовый портрет и для чего его строят?
Фазовый портрет — это графическое представление траекторий динамической системы в фазовом пространстве. Он помогает понять поведение системы в зависимости от начальных условий, показывая, как система развивается с течением времени. Это полезный инструмент для анализа устойчивости и возможных состояний системы, таких как равновесие или циклические колебания.
Какие библиотеки Python могут помочь в построении фазового портрета?
Для построения фазового портрета в Python обычно используют библиотеки, такие как Matplotlib для визуализации графиков, NumPy для численных вычислений и SciPy для решения дифференциальных уравнений. Эти инструменты позволяют легко реализовать построение траекторий и анализировать динамическое поведение системы.
Как можно построить фазовый портрет системы с двумя переменными в Python?
Для построения фазового портрета системы с двумя переменными в Python, сначала нужно задать систему дифференциальных уравнений, описывающих поведение этих переменных. Затем с помощью библиотеки SciPy решаем систему для разных начальных условий и отображаем полученные траектории на графике с помощью Matplotlib. Пример кода для такой задачи можно найти в документации SciPy.
Что такое «стабильность» и как её можно анализировать с помощью фазового портрета?
Стабильность в контексте фазового портрета означает, как система ведет себя вблизи равновесных точек. Если система возвращается в равновесие после небольшого отклонения, то точка считается стабильной. В фазовом портрете стабильность можно оценить, наблюдая за поведением траекторий около этих точек. Если траектории направляются к точке равновесия, она стабильна, если же уходят от неё — неустойчива.
Можно ли построить фазовый портрет для нелинейной системы в Python?
Да, Python прекрасно подходит для построения фазовых портретов нелинейных систем. Для этого нужно решить соответствующие нелинейные дифференциальные уравнения, используя численные методы, такие как метод Рунге-Кутты, которые реализованы в SciPy. Визуализация таких систем в Matplotlib позволяет увидеть, как ведут себя траектории в сложных динамических системах.
Что такое фазовый портрет и зачем его строить для динамических систем в Python?
Фазовый портрет — это графическое представление траекторий динамической системы в фазовом пространстве. Он позволяет понять поведение системы при различных начальных условиях. В Python для построения фазового портрета используют различные библиотеки, такие как Matplotlib и SciPy. Такой портрет помогает визуализировать устойчивость точек равновесия, а также выявлять типы аттракторов, например, устойчивые или неустойчивые. Он полезен для анализа как простых, так и более сложных динамических систем, таких как системы с нелинейными уравнениями.
Какие шаги нужно предпринять, чтобы построить фазовый портрет в Python для системы дифференциальных уравнений?
Для построения фазового портрета в Python нужно выполнить несколько шагов. Во-первых, необходимо задать систему дифференциальных уравнений, которые описывают динамическую систему. Это можно сделать с помощью функции, которая возвращает производные переменных в системе. Затем используется интегратор (например, из библиотеки SciPy), чтобы вычислить траектории системы для разных начальных условий. После этого результат интегрирования можно визуализировать с помощью библиотеки Matplotlib, построив графики переменных системы относительно друг друга, что и представляет собой фазовый портрет. Важно правильно выбрать параметры системы и начальные условия для получения полной картины ее поведения.