Фракталы – это геометрические объекты, структура которых повторяется на разных масштабах. Один из простейших способов их генерации – рекурсивные алгоритмы. В Python такие структуры удобно строить с помощью библиотеки turtle, обеспечивающей элементарную графику, и matplotlib, если требуется статичная визуализация.
Для реализации, например, кривой Коха достаточно определить рекурсивную функцию, делящую отрезок на три равные части и заменяющую среднюю на «выступ» в форме равностороннего треугольника. Уже на четвёртом уровне рекурсии получается фигура с более чем 2000 сегментами. Такая детализация требует точного контроля глубины вложенности, чтобы избежать переполнения стека или чрезмерного времени исполнения.
Работа с фракталами в Python требует понимания принципов рекурсии и особенностей вычислений с плавающей точкой. Для точной геометрии рекомендуется использовать decimal.Decimal вместо float, особенно при генерации фракталов с большим числом итераций. Это позволяет избежать накопления ошибок при многократных преобразованиях координат.
Оптимизация построения возможна через мемоизацию промежуточных результатов или предварительную генерацию координат с последующим отрисовыванием. В случае интерактивной графики целесообразно использовать Pygame или tkinter, если важна реакция интерфейса на действия пользователя.
Выбор типа фрактала: дерево, Коха или Мандельброта
При построении фракталов на Python целесообразно заранее определить, какой тип структуры требуется: дерево Пифагора, кривая Коха или множество Мандельброта. Выбор влияет на используемые библиотеки, производительность и способ визуализации.
Фрактальное дерево удобно реализовать через рекурсию с использованием библиотеки turtle или matplotlib. Оно требует минимальных вычислений, но подходит только для демонстрации рекурсивных принципов и простых геометрических конструкций. Основные параметры: угол разветвления, длина ветви, глубина рекурсии. Для интерактивности можно использовать tkinter.
Кривая Коха реализуется на основе поэтапной замены отрезков, что делает её подходящей для пошаговой генерации. Используются matplotlib или pygame. Каждый шаг увеличивает число отрезков в 4 раза, поэтому при глубине больше 5 может потребоваться оптимизация через отложенный рендеринг.
Множество Мандельброта требует комплексных чисел и плотных вычислений. Реализация возможна через numpy и отрисовку с matplotlib.pyplot.imshow или PIL.Image. Для ускорения желательно использовать векторизацию и задавать ограниченную область комплексной плоскости, например от -2 до 1 по оси X и от -1.5 до 1.5 по оси Y. Оптимальная сетка – 1000×1000 точек, число итераций – от 50 до 500 в зависимости от требуемой детализации.
Если цель – простая визуализация рекурсии, подойдёт дерево. Для построения с геометрической симметрией – кривая Коха. При интересе к комплексной плоскости и численным методам – множество Мандельброта.
Настройка среды: библиотеки и конфигурация проекта

Установите Python не ниже версии 3.10. Для работы с графикой потребуется matplotlib или pygame – в зависимости от способа визуализации. Для расчётов удобно использовать numpy. Установка выполняется через pip:
pip install numpy matplotlib
Если выбран pygame для интерактивной отрисовки, вместо matplotlib установите:
pip install pygame
Создайте виртуальное окружение в корне проекта:
python -m venv venv
Активируйте окружение:
Windows: venv\Scripts\activate
Linux/macOS: source venv/bin/activate
Структура проекта:
fractal_project/
venv/ – виртуальное окружение
main.py – точка входа
fractal/ – модуль с логикой построения
config.py – параметры отрисовки и масштабирования
В config.py вынесите значения: размеры окна, глубину рекурсии, цветовую схему. Это упростит модификацию без правки основного кода.
import logging
logging.basicConfig(filename=»fractal.log», level=logging.INFO)
Работайте в IDE с поддержкой автодополнения: PyCharm или VS Code с установленным расширением Python.
Рекурсивная генерация фрактала через функции

Рекурсия – ключевой механизм при построении фракталов. Она позволяет описывать самоподобные структуры через вызов функции внутри самой себя. Для корректной реализации требуется чёткое определение базового случая и правила деления фигуры.
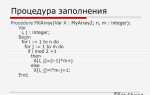
Пример: генерация кривой Коха. Исходный отрезок делится на три части. Средняя заменяется равнобедренным треугольником без основания. Функция принимает параметры: координаты начала и конца отрезка, текущую глубину, максимальную глубину рекурсии.
Кодовая структура:
def koch(x1, y1, x2, y2, depth):
if depth == 0:
draw_line(x1, y1, x2, y2)
return
dx = (x2 - x1) / 3
dy = (y2 - y1) / 3
x3 = x1 + dx
y3 = y1 + dy
x5 = x2 - dx
y5 = y2 - dy
x4 = (x3 + x5) / 2 - (y5 - y3) * (3 ** 0.5) / 2
y4 = (y3 + y5) / 2 + (x5 - x3) * (3 ** 0.5) / 2
koch(x1, y1, x3, y3, depth - 1)
koch(x3, y3, x4, y4, depth - 1)
koch(x4, y4, x5, y5, depth - 1)
koch(x5, y5, x2, y2, depth - 1)Функция draw_line должна быть реализована отдельно. Она отвечает за отрисовку отрезков в зависимости от используемой графической библиотеки, например, turtle, matplotlib или Pygame.
При глубине рекурсии более 6 может возникнуть ощутимая нагрузка на процессор и память. Рекомендуется заранее устанавливать ограничение и следить за производительностью, особенно при отрисовке в реальном времени.
Использование модуля turtle для визуализации

Модуль turtle входит в стандартную библиотеку Python и позволяет управлять графическим «черепаховым» исполнителем для построения фигур с помощью команд перемещения и поворота. Для построения фракталов удобно использовать рекурсивные функции, комбинируя их с командами forward() и left()/right().
Перед началом необходимо отключить анимацию с помощью tracer(0, 0) для ускорения отрисовки и вызвать update() после завершения построения. Это особенно важно при высокой глубине рекурсии. Пример инициализации:
from turtle import *
speed(0)
tracer(0, 0)
hideturtle()
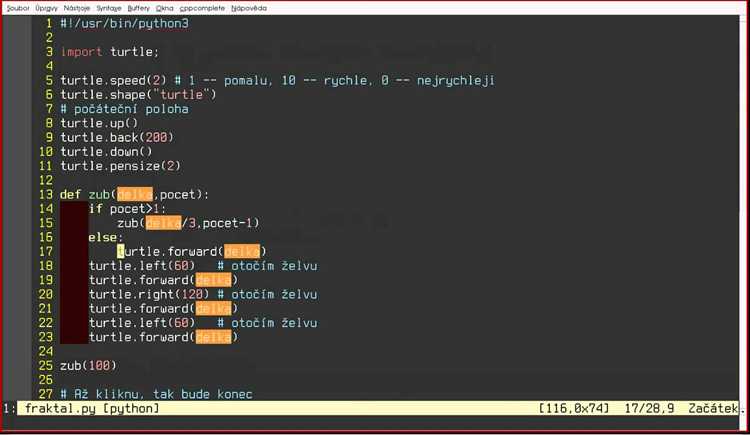
Для построения кривой Коха, базовая функция может выглядеть следующим образом:
def koch(length, depth):
if depth == 0:
forward(length)
else:
length /= 3
koch(length, depth - 1)
left(60)
koch(length, depth - 1)
right(120)
koch(length, depth - 1)
left(60)
koch(length, depth - 1)
Запуск визуализации осуществляется после позиционирования «черепахи»:
penup()
goto(-200, 0)
setheading(0)
pendown()
koch(400, 4)
update()
done()
Рекомендуется использовать hideturtle() для скрытия указателя и speed(0) для максимальной скорости. При сложных фракталах настройка размеров окна (setup()) и координатной системы (setworldcoordinates()) может понадобиться для отображения полной структуры.
Отображение фрактала Мандельброта с помощью matplotlib
Для построения множества Мандельброта используется двумерная решётка комплексных чисел. Вычисления выполняются по формуле z = z2 + c, где z – последовательные значения, а c – координаты на плоскости. Начальное значение z равно нулю. Для каждого c проверяется, не выходит ли z за пределы модуля 2 в течение заданного числа итераций.
Создайте сетку комплексных чисел с помощью numpy. Например, диапазон [-2, 1] по оси x и [-1.5, 1.5] по оси y при разрешении от 500×500 и выше. Используйте numpy.linspace и numpy.meshgrid.
Для отображения результатов применяйте matplotlib.pyplot.imshow с параметром cmap='hot' или cmap='inferno' для повышения контрастности. Массив значений должен содержать количество итераций до выхода за пределы, либо максимальное число итераций, если значение удержалось.
Рекомендуемая глубина итераций – от 100 до 1000, в зависимости от точности и времени выполнения. Для оптимизации используйте numba или multiprocessing, особенно при высоком разрешении.
Параметры управления глубиной и масштабом

Глубина (или итерации) – это количество повторений вычислений для каждого пикселя. Чем больше глубина, тем более сложным и детализированным будет фрактал. Однако с увеличением глубины растет нагрузка на процессор, что может значительно замедлить вычисления. Поэтому важно выбрать оптимальное значение, которое позволит достичь нужной детализации без чрезмерных затрат времени.
Масштаб регулирует размер области, которую охватывает фрактал. Изменяя масштаб, можно увидеть разные части фрактала с разной степенью детализации. При увеличении масштаба фрактал становится более подробным, а при уменьшении – более обобщенным.
- Для фрактала Мандельброта глубина может варьироваться от 50 до 1000 итераций, в зависимости от того, сколько деталей вы хотите увидеть. При значении 1000 вы получите почти идеальное изображение, но оно будет строиться значительно дольше.
- Масштаб следует изменять, исходя из требуемой области исследования. Если вам нужно рассмотреть лишь центральную часть фрактала, достаточно уменьшить область. Для исследования фрактала на его краях потребуется большее увеличение.
Рекомендации:
- Используйте оптимизированные алгоритмы для вычисления фракталов, такие как алгоритм с ранним выходом, чтобы ускорить процесс при высоких значениях глубины.
- При масштабировании важно учитывать точность: слишком высокий масштаб может привести к потере контекста изображения, а слишком низкий – к его размытию.
- Для быстрого тестирования работы фрактала лучше начать с небольшой глубины (50-100) и постепенно увеличивать ее по мере необходимости.
Глубина и масштаб в совокупности определяют, насколько точным и красивым будет фрактал. Правильная настройка этих параметров – это баланс между качеством и производительностью.
Для сохранения фрактала в изображение с помощью Python, можно использовать библиотеку matplotlib, которая предоставляет удобные функции для рендеринга и экспорта изображений. Например, после построения фрактала, чтобы сохранить изображение, можно воспользоваться функцией savefig(). Этот метод позволяет указать путь и формат файла, в который будет сохранён фрактал.
Пример кода для сохранения изображения:
import matplotlib.pyplot as plt
import numpy as np
# Функция для генерации фрактала (например, Мандельброт)
def mandelbrot(c, max_iter):
z = 0
for n in range(max_iter):
if abs(z) > 2:
return n
z = z*z + c
return max_iter
# Генерация фрактала
width, height = 800, 800
image = np.zeros((height, width))
for x in range(width):
for y in range(height):
c = complex((x - width / 2) * 4.0 / width, (y - height / 2) * 4.0 / height)
image[y, x] = mandelbrot(c, 256)
# Отображение фрактала
plt.imshow(image, cmap='hot', extent=(-2, 2, -2, 2))
plt.savefig('fractal.png', dpi=300) # Сохранение фрактала в файл
plt.show()
Этот код генерирует фрактал Мандельброта и сохраняет его в файл «fractal.png» с разрешением 300 dpi. Для изменения формата файла, достаточно указать расширение, например, .jpg или .svg.
Пример интерактивного графика с использованием plotly:
import plotly.graph_objects as go import numpy as np # Генерация данных для фрактала x = np.linspace(-2, 2, 800) y = np.linspace(-2, 2, 800) X, Y = np.meshgrid(x, y) Z = np.zeros(X.shape) for i in range(X.shape[0]): for j in range(X.shape[1]): Z[i, j] = mandelbrot(complex(X[i, j], Y[i, j]), 256) # Создание интерактивного графика fig = go.Figure(data=go.Surface(z=Z, x=X, y=Y, colorscale='Hot')) fig.update_layout(title='Фрактал Мандельброта', autosize=True) fig.show()
Этот пример позволяет интерактивно исследовать фрактал с помощью 3D-панели, изменяя угол обзора и масштаб. Такие графики могут быть полезны для более глубокого изучения структуры фракталов и их особенностей.
Вопрос-ответ:
Что такое фрактал и как его можно построить с использованием Python?
Фрактал — это фигура, которая обладает самоподобием на различных уровнях масштабирования. То есть, увеличивая часть фрактала, можно увидеть схожие формы, как и в его целом виде. Для построения фракталов с помощью Python часто используют библиотеки, такие как `matplotlib` для визуализации и `numpy` для математических вычислений. Один из самых популярных фракталов — это множество Мандельброта, которое строится на основе простых математических формул и повторяющихся итераций. В Python можно создать такой фрактал, используя циклы и функции для вычислений, а затем отобразить результат с помощью графиков.
Какие проблемы могут возникнуть при создании фрактала в Python?
При создании фракталов в Python могут возникнуть несколько проблем. Например, большое количество итераций при вычислении может привести к долгому времени работы программы. Чтобы ускорить процесс, можно уменьшить разрешение изображения или ограничить количество итераций. Также может возникнуть проблема с памятью, особенно если создаются очень большие изображения или используются сложные алгоритмы. В таких случаях полезно использовать более эффективные методы хранения данных, например, сжатие данных или использование многозадачности для параллельных вычислений. Иногда также бывает трудно добиться нужной точности в расчетах, поэтому важно тщательно настроить параметры, такие как максимальное количество итераций или пределы для проверки на выход за бесконечность.
Какие библиотеки Python лучше всего использовать для построения фракталов?
Для построения фракталов на Python чаще всего используют несколько библиотек, каждая из которых решает определённые задачи. Одной из самых популярных является **Matplotlib**, которая предоставляет инструменты для визуализации данных, включая изображения фракталов. Также часто используют **NumPy** для работы с массивами и выполнения математических операций, необходимых для построения фракталов. Если необходимо ускорить вычисления, то можно использовать **Cython** или **Numba**, которые позволяют ускорить выполнение кода за счёт компиляции в машинный код. Для создания более сложных фракталов, например, фракталов в трёх измерениях, можно использовать библиотеку **Mayavi**, которая предназначена для 3D-визуализации. Все эти библиотеки хорошо интегрируются между собой, и их использование зависит от сложности задачи и требуемого качества визуализации.