Как сгенерировать выборку нормального распределения python

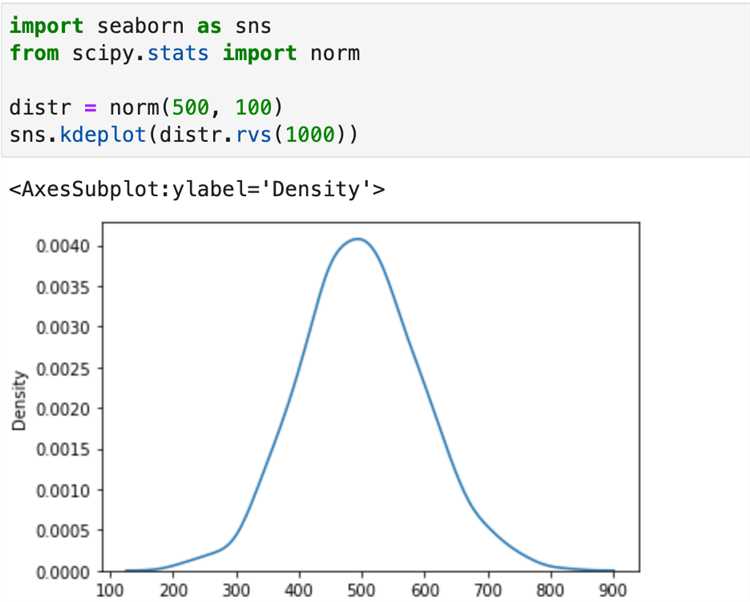
Для работы с нормальным распределением в Python используется несколько подходов, наиболее эффективный из которых – это использование библиотеки NumPy. С помощью этой библиотеки можно легко генерировать выборки, параметры которых полностью контролируются, включая среднее значение и стандартное отклонение. Однако для того, чтобы правильно сгенерировать выборку, важно понимать, как именно эти параметры влияют на форму распределения и какие функции стоит использовать в зависимости от конкретных задач.

Основной функцией для генерации выборки из нормального распределения является numpy.random.normal. Эта функция принимает три обязательных параметра: среднее значение (mu), стандартное отклонение (sigma) и количество генерируемых элементов (size). Например, чтобы получить выборку из 1000 значений с средним 0 и стандартным отклонением 1, достаточно выполнить команду:

import numpy as np
sample = np.random.normal(0, 1, 1000)

После выполнения кода в переменной sample окажется массив из 1000 чисел, которые распределены по нормальному закону. Важно отметить, что сгенерированные данные будут случайными, но их статистические свойства (среднее и стандартное отклонение) будут приближаться к указанным параметрам по мере увеличения размера выборки.

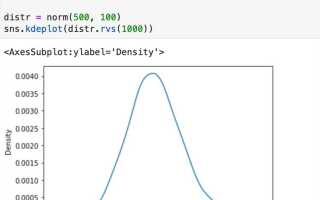
Для анализа и визуализации полученной выборки удобно использовать библиотеки Matplotlib или Seaborn. Визуализация позволяет наглядно оценить распределение данных и убедиться в том, что они действительно следуют нормальному закону. Пример построения гистограммы:

import matplotlib.pyplot as plt
plt.hist(sample, bins=30, density=True)
plt.show()

С помощью этой техники можно не только создать выборку, но и оценить ее распределение, что полезно для дальнейшего анализа статистических данных. Выбирая параметры для генерации выборки, важно помнить о масштабе данных, так как это напрямую влияет на точность результатов в моделировании реальных процессов.

Использование библиотеки NumPy для генерации выборки

Библиотека NumPy предоставляет функцию numpy.random.normal, которая позволяет легко генерировать выборки, следуя нормальному распределению. Эта функция принимает три основных параметра: среднее значение, стандартное отклонение и размер выборки. Рассмотрим примеры использования и основные рекомендации.

Для генерации выборки с нормальным распределением нужно вызвать функцию numpy.random.normal(loc=0.0, scale=1.0, size=None). Параметр loc задает среднее значение (μ), scale – стандартное отклонение (σ), а size указывает количество элементов в выборке. Например, чтобы получить выборку из 1000 значений с средним 0 и стандартным отклонением 1, используем следующий код:

import numpy as np
sample = np.random.normal(loc=0, scale=1, size=1000)

Этот код создаст массив из 1000 элементов, распределенных по нормальному закону с заданными параметрами. Важно отметить, что размер выборки указывается как целое число, и если он не задан, функция вернет одно случайное значение.

Для контроля качества сгенерированных данных полезно построить гистограмму выборки. Использование matplotlib для визуализации помогает убедиться, что данные действительно следуют нормальному распределению. Пример кода для построения гистограммы:

import matplotlib.pyplot as plt
plt.hist(sample, bins=30, density=True)
plt.show()

При работе с реальными данными часто необходимо исследовать распределение и корректировать параметры. Например, для выборки с другим средним или стандартным отклонением достаточно изменить соответствующие параметры loc и scale. Если нужно создать выборку с большим размером, это также легко реализуется, передав нужное число в параметр size.

Помимо стандартной генерации данных с нормальным распределением, numpy.random.normal позволяет задавать другие полезные параметры, такие как генерация данных с учетом корреляции или зависимостей. Для этого можно использовать другие функции NumPy или дополнительные методы для обработки выборок, такие как методы для масштабирования или центровки данных.

Настройка параметров нормального распределения (среднее и стандартное отклонение)

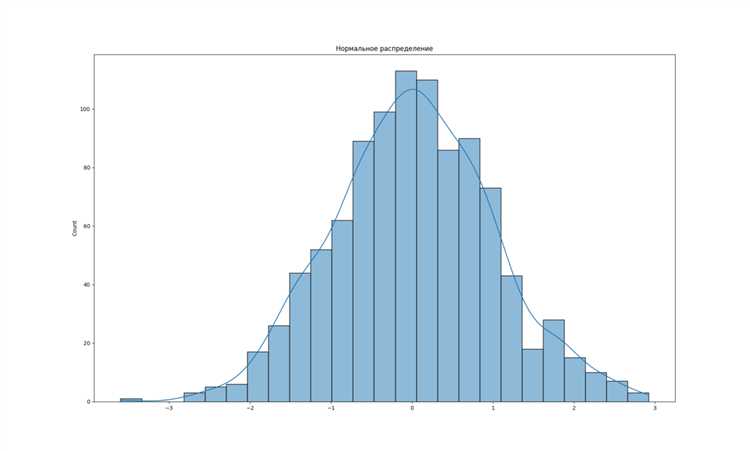
Нормальное распределение описывается двумя основными параметрами: средним (μ) и стандартным отклонением (σ). Эти параметры определяют форму распределения и важны для генерации случайных данных, отражающих реальные процессы.

Среднее значение (μ) указывает на центральное положение распределения. Оно определяет, где расположена основная масса значений. В Python для задания среднего при генерации выборки из нормального распределения используется параметр loc. Например, если нужно сгенерировать выборку с средним 10, то параметр будет равен 10.

Стандартное отклонение (σ) характеризует степень разброса значений относительно среднего. Чем больше σ, тем шире будет распределение, и наоборот. В Python стандартное отклонение задается через параметр scale. Для выборки с небольшим разбросом значений можно установить σ равным 2, для большего – 5.

Пример генерации выборки с заданным средним и стандартным отклонением:

import numpy as np
sample = np.random.normal(loc=10, scale=2, size=1000)

В этом примере loc=10 задает среднее, а scale=2 – стандартное отклонение. Размер выборки равен 1000.

При настройке этих параметров важно учитывать, что значения среднего и стандартного отклонения напрямую влияют на характер данных. Для задач, связанных с моделированием реальных явлений, важно корректно подобрать параметры, чтобы они соответствовали ожидаемому поведению процесса.

Если требуется сгенерировать выборку с разными значениями среднего и стандартного отклонения для различных подмножеств данных, достаточно изменять параметры loc и scale в соответствии с нуждами задачи.

Генерация выборки с заданным размером

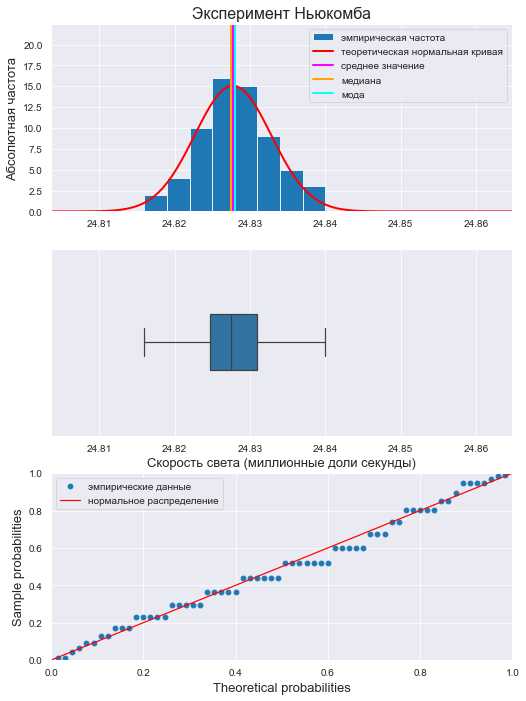
Для создания выборки нормального распределения с конкретным размером в Python используется функция numpy.random.normal(). Эта функция позволяет задать количество элементов в выборке через параметр size, а также задать среднее значение (по умолчанию 0) и стандартное отклонение (по умолчанию 1).

Пример кода для генерации выборки из 1000 элементов с нормальным распределением с средним 10 и стандартным отклонением 2:

import numpy as np
sample = np.random.normal(loc=10, scale=2, size=1000)

Здесь loc – это среднее значение, scale – стандартное отклонение, а size – размер выборки. Важно помнить, что параметр size может быть как целым числом, так и кортежем для генерации многомерных массивов. Например, size=(100, 5) создаст массив размером 100 на 5.

Для контроля над случайностью, при необходимости, можно установить генератор случайных чисел с помощью numpy.random.seed(). Это обеспечит воспроизводимость результатов при многократном запуске кода с одинаковыми параметрами.

np.random.seed(42)
sample = np.random.normal(loc=10, scale=2, size=1000)

Визуализация выборки с помощью гистограммы

Для анализа выборки нормального распределения часто используется гистограмма, так как она позволяет быстро оценить форму распределения данных. В Python для построения гистограммы удобно использовать библиотеку Matplotlib. Рассмотрим пример, как визуализировать выборку с помощью гистограммы.

Предположим, у нас есть выборка из 1000 элементов, сгенерированная с использованием функции numpy.random.normal(). Чтобы построить гистограмму, сначала необходимо импортировать соответствующие библиотеки:

import numpy as np
import matplotlib.pyplot as plt

Далее создадим выборку:

data = np.random.normal(loc=0, scale=1, size=1000)

Вызвав функцию plt.hist(), можно построить гистограмму:

plt.hist(data, bins=30, edgecolor='black', alpha=0.7)
plt.title('Гистограмма выборки нормального распределения')
plt.xlabel('Значения')
plt.ylabel('Частота')
plt.show()

Параметр bins определяет количество столбцов на гистограмме. Значение 30 в данном случае оптимально для 1000 элементов, но оно может быть скорректировано в зависимости от размера выборки и необходимой детализации. Чем больше значений в параметре bins, тем более детализированным будет отображение частот, но слишком большое количество интервалов может привести к излишней «шумности» графика.

Также стоит обратить внимание на параметр alpha, который регулирует прозрачность столбцов. Значение 0.7 позволяет добиться более четкого визуального восприятия данных. Параметр edgecolor помогает выделить края столбцов, делая их более заметными.

Визуализируя выборку нормального распределения, вы сможете увидеть, насколько хорошо она соответствует теоретической нормальной кривой. Для этого можно наложить на гистограмму плотность вероятности, которая будет отображать идеальную форму нормального распределения. Это можно сделать с помощью функции scipy.stats.norm.pdf():

from scipy.stats import norm
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, loc=0, scale=1)
plt.hist(data, bins=30, edgecolor='black', alpha=0.7, density=True)
plt.plot(x, p, 'k', linewidth=2)
plt.title('Гистограмма с плотностью нормального распределения')
plt.xlabel('Значения')
plt.ylabel('Частота')
plt.show()

Такой подход позволяет сравнить гистограмму с теоретическим распределением, наглядно оценивая, насколько сгенерированные данные соответствуют нормальному распределению. Подобная визуализация помогает выявить отклонения от теоретической модели и оптимизировать процесс генерации данных для дальнейшего анализа.

Проверка нормальности распределения выборки

Проверка нормальности распределения выборки – важный этап анализа данных. Это необходимо для использования статистических методов, основанных на предположении о нормальном распределении. Существует несколько способов оценки нормальности: визуальные методы и статистические тесты.

Для визуальной проверки нормальности можно использовать гистограмму и Q-Q график. На гистограмме должна быть видна симметричная колоколообразная форма, если данные распределены нормально. Q-Q график помогает увидеть, насколько близки к нормальному распределению квантильные значения данных и теоретические квантильные значения нормального распределения.

Однако визуальные методы не всегда дают точные результаты, особенно для больших выборок. Поэтому часто применяют статистические тесты.

• Тест Шапиро-Уилка – один из самых популярных тестов для проверки нормальности. Его результат основан на сравнении выборки с нормальным распределением. Если p-значение теста меньше 0.05, то гипотеза о нормальности отвергается.
• Тест Колмогорова-Смирнова проверяет, насколько сильно данные отклоняются от теоретического нормального распределения. Этот тест также предоставляет p-значение для оценки статистической значимости отклонений.
• Тест Андерсона-Дарлинга является модификацией теста Колмогорова-Смирнова и более чувствителен к отклонениям в хвостах распределения. Он может быть полезен при работе с данными, где хвосты играют важную роль.

Для применения этих тестов в Python можно использовать библиотеку scipy.stats. Пример использования теста Шапиро-Уилка:

from scipy import stats
data = [10, 12, 9, 8, 11, 15, 16, 14, 13, 12]
stat, p_value = stats.shapiro(data)
if p_value < 0.05:
print("Распределение не является нормальным")
else:
print("Распределение нормально")

Если выборка большая, то можно также применить тесты на основе асимптотической теории, такие как тест Лиллиефорса.

При проверке нормальности важно учитывать размер выборки. Для малых выборок (до 30 элементов) тесты могут давать ложные результаты. Для больших выборок (более 1000) нормальность можно оценивать не только через тесты, но и через характеристики данных, такие как асимметрия и эксцесс.

Если выборка не проходит тест на нормальность, можно использовать методы преобразования данных (например, логарифмическое преобразование) или применить непараметрические методы, которые не требуют нормальности распределения.

Сравнение теоретического и эмпирического распределений

Для оценки соответствия сгенерированной выборки нормальному распределению используют визуализацию и количественные метрики. Построим гистограмму выборки и наложим на неё теоретическую плотность распределения, рассчитанную через scipy.stats.norm.pdf с параметрами, совпадающими со средним и стандартным отклонением выборки.

Пример кода:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
sample = np.random.normal(loc=0, scale=1, size=1000)
mean, std = np.mean(sample), np.std(sample)
x = np.linspace(min(sample), max(sample), 100)
pdf = norm.pdf(x, loc=mean, scale=std)
plt.hist(sample, bins=30, density=True, alpha=0.6, label="Эмпирическая гистограмма")
plt.plot(x, pdf, 'r-', lw=2, label="Теоретическая плотность")
plt.legend()
plt.show()

Для количественной проверки применяют критерий Колмогорова-Смирнова:

from scipy.stats import kstest
statistic, p_value = kstest(sample, 'norm', args=(mean, std))
print(f"Статистика K-S: {statistic:.4f}, p-значение: {p_value:.4f}")

Если p > 0.05, то гипотеза о нормальности не отвергается. Также полезен Q-Q график для визуального анализа отклонений:

import scipy.stats as stats
stats.probplot(sample, dist="norm", plot=plt)
plt.show()

Совпадение точек с диагональю указывает на нормальность распределения. При систематических отклонениях необходим пересмотр параметров генерации или размера выборки.

Генерация выборки с использованием других библиотек (например, SciPy)

Библиотека scipy.stats предоставляет более гибкий функционал для работы с нормальным распределением по сравнению с numpy. Объект scipy.stats.norm позволяет не только генерировать случайные значения, но и использовать параметры распределения напрямую без необходимости стандартных преобразований.

Пример генерации выборки из нормального распределения с математическим ожиданием 10 и стандартным отклонением 2:

from scipy.stats import norm
sample = norm.rvs(loc=10, scale=2, size=1000)

В отличие от numpy.random.normal, объект norm позволяет использовать методы для получения дополнительных характеристик:

mean = norm.mean(loc=10, scale=2)
std = norm.std(loc=10, scale=2)
pdf_val = norm.pdf(10, loc=10, scale=2)  # значение плотности вероятности
cdf_val = norm.cdf(10, loc=10, scale=2)  # значение функции распределения

Для получения воспроизводимых результатов можно зафиксировать генератор случайных чисел:

sample = norm.rvs(loc=10, scale=2, size=1000, random_state=42)

При необходимости использования генерации в векторизованном виде с поддержкой broadcasting, SciPy корректно обрабатывает массивы параметров:

import numpy as np
locs = np.array([0, 5, 10])
scales = np.array([1, 2, 3])
samples = norm.rvs(loc=locs[:, None], scale=scales[:, None], size=(3, 1000))

Такой подход удобен при генерации выборок с различными параметрами для моделирования множественных распределений одновременно.

Оптимизация генерации выборки для больших данных

При работе с выборками нормального распределения объемом в миллионы элементов критично учитывать производительность и использование памяти. Базовая функция numpy.random.normal подходит для большинства задач, но при масштабировании требует оптимизации.

• Используйте параметр size как кортеж для генерации массивов высокой размерности, например: size=(10000, 1000). Это быстрее, чем последовательные вызовы генерации меньших массивов.
• При необходимости генерации из стандартного нормального распределения (среднее = 0, σ = 1), предпочтительнее numpy.random.randn, так как она быстрее за счет отсутствия дополнительных параметров.
• В многопоточном окружении предпочтительнее использовать numpy.random.Generator вместо устаревшего RandomState. Это снижает накладные расходы и повышает воспроизводимость при параллельной обработке.
• Для обработки объемов данных, превышающих доступную оперативную память, используйте генерацию по частям (батчами). Например, итеративно генерировать блоки по 1 млн значений и сохранять их на диск с помощью numpy.save или в формате HDF5 через h5py.
• На GPU можно задействовать cupy.random.normal при наличии NVIDIA CUDA. Это позволяет многократно ускорить генерацию выборок объемом в десятки миллионов точек.
• Избегайте преобразования типа массива после генерации. Сразу указывайте нужный dtype (например, float32) в Generator.normal через astype в цепочке вызова, чтобы избежать лишнего копирования памяти.

Реализация вышеуказанных подходов позволяет сократить время генерации выборки в 2–5 раз при объеме более 10⁷ значений и уменьшить потребление памяти до 50% за счет использования оптимального формата хранения и распределенной обработки.

Вопрос-ответ: