Как сделать дробь в html

Конечно! Вот готовый текст по вашему запросу:

htmlEdit

Выбор монитора для работы зависит от типа задач. Для офисных приложений подойдет экран с диагональю 23–27 дюймов и разрешением не ниже Full HD (1920×1080). Если основная деятельность связана с графикой, стоит обратить внимание на панели IPS с разрешением от 2560×1440 пикселей и точной цветопередачей (покрытие sRGB не менее 99%).

Частота обновления играет второстепенную роль при выборе офисного монитора, но при длительной работе за компьютером рекомендуется выбирать модели с частотой 75 Гц и выше, чтобы снизить нагрузку на глаза. Приоритетной характеристикой должна быть технология защиты зрения: Flicker-Free для устранения мерцания и Low Blue Light для снижения синего излучения.

При выборе размеров экрана нужно учитывать рабочее пространство. Для небольших столов подходят модели до 24 дюймов, для крупных рабочих мест – от 27 до 32 дюймов. Кривизна экрана (1800R–3000R) актуальна для широкоформатных мониторов, если требуется одновременно работать с несколькими окнами без дополнительных дисплеев.

Важным критерием остается тип подключения. Современные мониторы должны поддерживать порты DisplayPort 1.2/1.4 или HDMI 2.0/2.1. Для ноутбуков удобен USB-C с функцией Power Delivery, позволяющий одновременно передавать изображение и заряжать устройство.

Оптимальной плотностью пикселей для повседневной работы считается значение от 90 до 110 PPI. При выборе 4K-монитора на 27 дюймах плотность достигает около 163 PPI, что делает изображение сверхчетким, но требует масштабирования интерфейса в настройках операционной системы.

Хотите, я еще дополнительно подготовлю следующий блок статьи в таком же формате? 🚀

htmlEditКак сделать дробь в HTML

Для создания дробей в HTML можно использовать несколько способов в зависимости от задачи. Самый простой вариант – символы юникода. Например, дробь одна вторая можно вставить с помощью ½ (½).

Если требуется произвольная дробь, которую нельзя заменить готовым символом, лучше применять тег  для числителя и  для знаменателя. Пример: 12/3 будет выглядеть как 1²/₃.

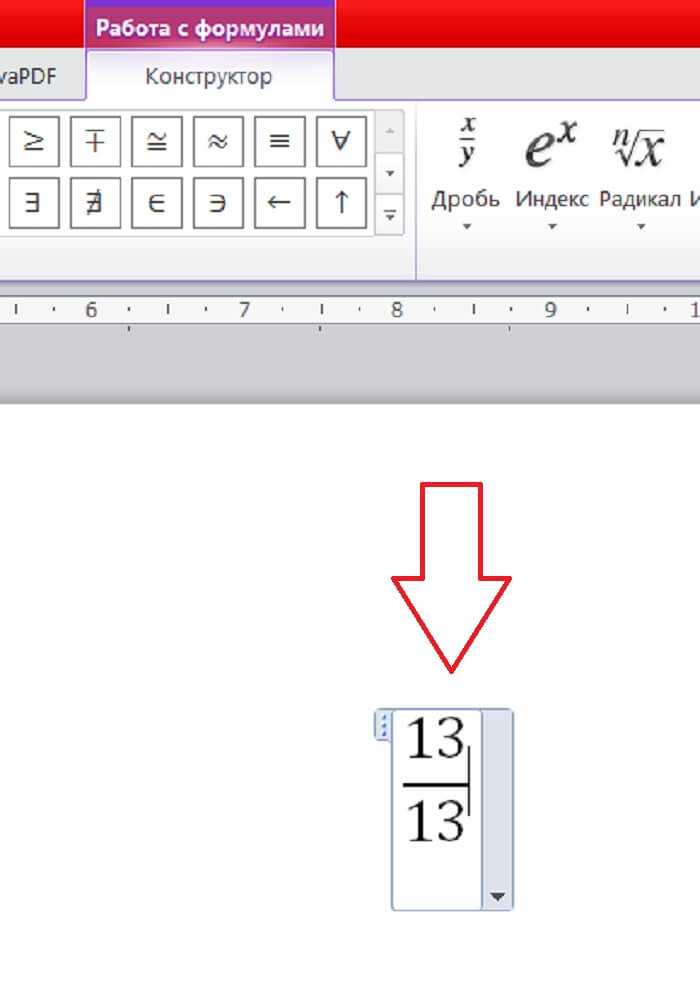
Более правильный способ для отображения математических дробей – использование элемента <math> языка MathML. Пример записи дроби ¾:

<math xmlns="http://www.w3.org/1998/Math/MathML"> <mfrac> <mn>3</mn> <mn>4</mn> </mfrac> </math>

MathML поддерживается не всеми браузерами одинаково, поэтому стоит учитывать совместимость, если проект рассчитан на широкую аудиторию.

Если нужна гибкая настройка внешнего вида дроби без использования MathML, можно оформить дробь через стилизацию с помощью тегов  и CSS, например, сделать числитель сдвинутым вверх, а знаменатель – вниз.

Простое отображение дроби с помощью тега и

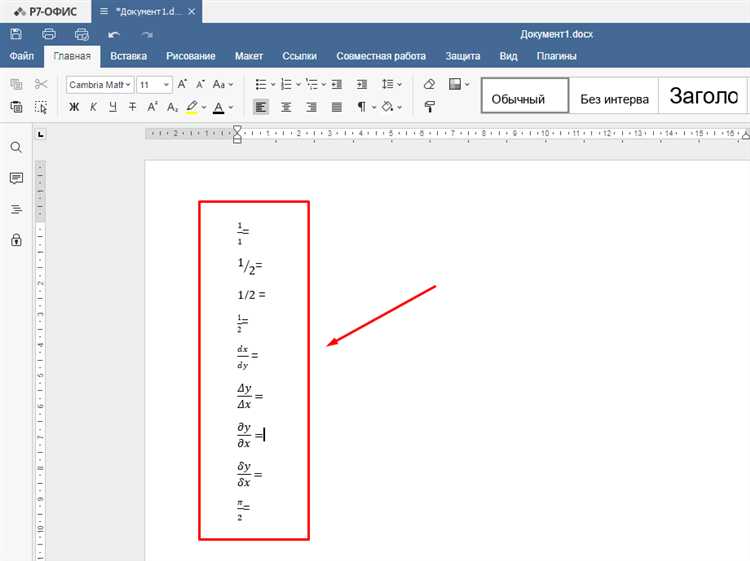
Для отображения простой дроби в HTML можно использовать теги  и , комбинируя их с косой чертой. Например, запись дроби 3/4 оформляется так: 3/4. Браузер отобразит её следующим образом: 3^/4.

Чтобы дробь выглядела аккуратнее, числитель можно вынести вверх с помощью , а знаменатель опустить вниз через . Например: 1/2. Это даст результат: ¹/₂.

Для более выразительного вида рекомендуется заключать всю дробь в контейнер  и при необходимости дополнительно корректировать её отображение через CSS, например, выравнивая положение элементов.

Этот способ подходит для статического контента и простых случаев. Для сложных дробей и математических формул лучше использовать MathML или специализированные библиотеки, такие как KaTeX или MathJax.

Использование символов Юникода для представления дробей

Юникод включает готовые символы для записи распространённых дробей, таких как ¼ (U+00BC), ½ (U+00BD) и ¾ (U+00BE). Они позволяют отображать дробные значения в тексте без необходимости использовать форматирование с косой чертой или дополнительные надстрочные и подстрочные знаки.

Для более редких дробей применяются символы из диапазона U+2150–U+215E. Например, ⅐ (U+2150) представляет одну седьмую, ⅑ (U+2151) – одну девятую, а ⅔ (U+2154) – две трети. Эти знаки воспринимаются как полноценные символы, что упрощает их обработку в цифровых документах и увеличивает совместимость при передаче данных между системами.

При необходимости отображать дроби, отсутствующие в стандарте Юникода, рекомендуется использовать обычную косую черту (/), например, «5/8». Однако следует помнить, что такой формат воспринимается как последовательность символов, а не как одна дробь, что может влиять на визуальное выравнивание и считывание текстов системами автоматической обработки.

Для корректного ввода дробных символов можно использовать коды Alt-клавиш в Windows (например, Alt+0188 для ¼) или вставку через панели символов в текстовых редакторах. В HTML-разметке дробные символы указываются через сущности, например, ¼ для ¼ или ⅔ для ⅔.

Выбор между готовыми дробями Юникода и текстовыми записями зависит от требований к визуальному качеству текста, совместимости с программами и удобству обработки данных. При оформлении математических текстов для веба рекомендуется применять символы Юникода там, где это возможно, чтобы сохранить компактность и читабельность записи.

Создание дроби через стилизацию с помощью CSS

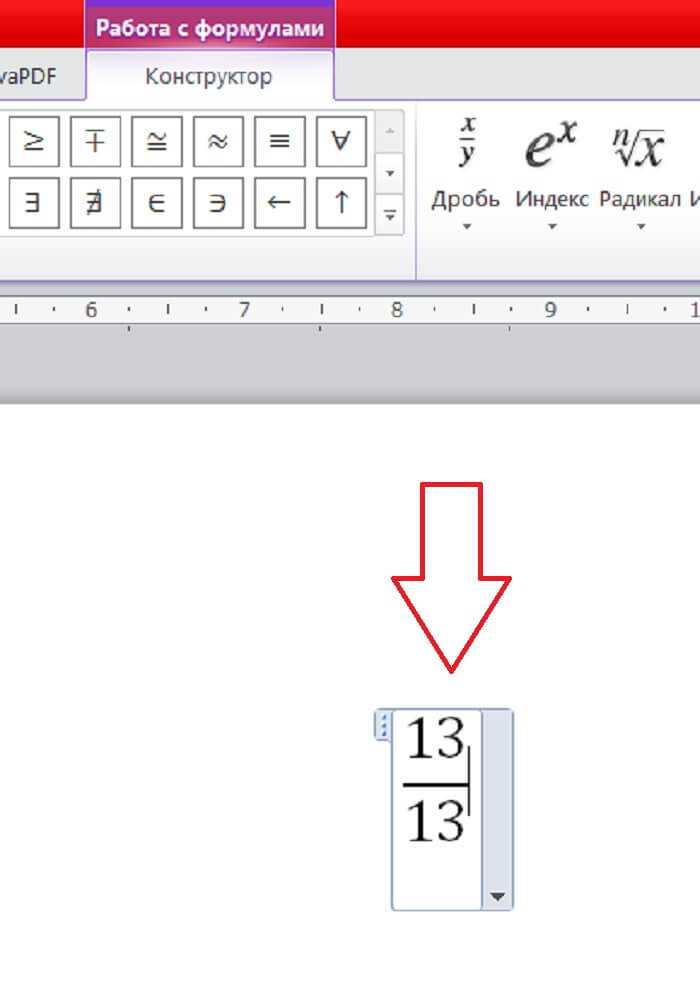
Для отображения дробей без использования изображений или сложной разметки можно применить стилизацию текста средствами CSS. Это позволяет добиться аккуратного визуального результата с минимальными усилиями.

Создайте контейнер с тегом  или <div>, в котором будет размещён числитель и знаменатель.
Для числителя используйте отдельный элемент с уменьшенным размером шрифта и выравниванием по нижней части базовой линии текста.
Знаменатель разместите ниже числителя с помощью вертикального позиционирования и аналогичного уменьшения шрифта.
Добавьте разделительную черту между числителем и знаменателем через псевдоэлемент ::after или ::before.

Пример разметки:

<span class="fraction">
<span class="numerator">1</span>
<span class="separator">/</span>
<span class="denominator">2</span>
</span>

Базовые стили:

.fraction {
display: inline-flex;
align-items: center;
font-size: 1em;
}
.numerator, .denominator {
font-size: 0.8em;
}
.separator {
margin: 0 2px;
}

Для более сложной стилизации можно применить вертикальное смещение:

.numerator {
transform: translateY(-30%);
}
.denominator {
transform: translateY(30%);
}

Альтернативный способ – использование свойства position: relative для числителя и знаменателя с указанием top или bottom для тонкой настройки положения.

Числитель приподнимается на 30–40% от линии базового текста.
Знаменатель опускается на аналогичное расстояние вниз.

Такой метод сохраняет адаптивность дроби при изменении размера шрифта на странице и легко масштабируется под разные задачи.

Верстка дроби с использованием таблицы

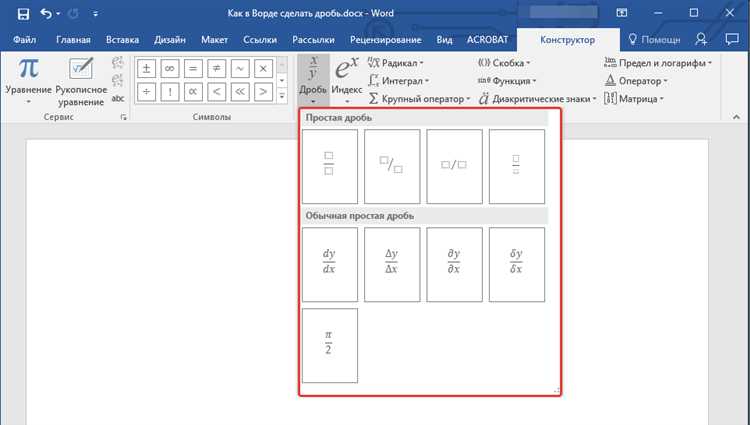
Для создания аккуратной дроби с помощью таблицы необходимо использовать элемент <table> с одной колонкой и двумя строками. В верхней строке размещается числитель, в нижней – знаменатель. Для центровки содержимого применяется атрибут align="center" или CSS-свойство text-align: center для ячеек <td>.

Пример разметки дроби 3/4:

<table cellpadding="0" cellspacing="0">
<tr>
<td align="center">3</td>
</tr>
<tr>
<td align="center">4</td>
</tr>
</table>

Рекомендуется обнулить внутренние отступы таблицы через cellpadding="0" и межячеечные расстояния через cellspacing="0", чтобы элементы дроби были плотно расположены друг над другом. Высоту строк можно регулировать через атрибут height или соответствующие CSS-свойства для достижения компактного вида.

Для увеличения читаемости дроби допустимо добавить горизонтальную линию между числителем и знаменателем, используя дополнительную строку с ячейкой, в которой размещается элемент <hr> с заданной шириной. Например:

<table cellpadding="0" cellspacing="0">
<tr>
<td align="center">3</td>
</tr>
<tr>
<td><hr width="50%" /></td>
</tr>
<tr>
<td align="center">4</td>
</tr>
</table>

Такой подход позволяет создать дробь без использования специальных символов или формул, обеспечивая при этом корректное отображение во всех браузерах, включая устаревшие версии.

Как сделать дробь адаптивной для мобильных устройств

Чтобы дробь корректно отображалась на мобильных устройствах, нужно учитывать особенности маленьких экранов и использовать минимальный набор HTML-разметки. Один из надёжных способов – применять встроенные элементы без использования графики.

Оптимальный вариант – оформить дробь с помощью тега  для числителя и  для знаменателя, поместив их в контейнер с небольшими адаптивными настройками через CSS.

Пример базовой структуры:

<span style="display:inline-flex;flex-direction:column;align-items:center;font-size:1em;">
<sup>1</sup>
<sub>2</sub>
</span>

При таком подходе дробь автоматически масштабируется вместе с текстом и остаётся читаемой на любых экранах без горизонтального скроллинга.

Для более сложных дробей с длинными числами лучше использовать контейнеры с управлением переносом текста. В этом случае добавляется свойство word-break: break-word; к основному элементу.

Если необходимо отобразить дробь, используя классическую горизонтальную черту, можно задействовать таблицу:

Эта структура позволяет дроби оставаться пропорциональной даже на узких экранах. Для лучшей адаптации шрифт таблицы можно сделать относительным к размеру родителя через font-size: 1em; или font-size: 5vw;.

Чтобы избежать обрезания дробей на сверхмаленьких устройствах, рекомендуется дополнительно ограничить минимальный размер шрифта через медиазапросы, например:

@media (max-width: 400px) {
span, table {
font-size: 4vw;
}
}

Итоговая задача – сохранить читаемость и пропорциональность дроби без перегрузки структуры лишними элементами и стилями.

Хочешь, я ещё покажу вариант для сложных дробей типа «12 3/8»? 🚀

Вставка дробей в текстовые поля и формы HTML

Для отображения дробей в текстовых полях и формах HTML можно использовать несколько подходов в зависимости от задач. Самый простой способ – использование специальных символов Юникода. Например, символы ¼ (U+00BC), ½ (U+00BD) и ¾ (U+00BE) вставляются напрямую в значение атрибута value тега <input> или внутри <textarea>.

Если требуется отображать более сложные дроби, например 5/8 или 7/16, стандартных символов недостаточно. В этом случае дробь записывается через обычную косую черту (/), например 5/8. При этом желательно контролировать форматирование через JavaScript, чтобы заменить косую черту на визуально корректное отображение дроби с помощью подстановки специальных символов или форматов Unicode.

Другой вариант – использовать надстрочные и подстрочные символы. Например, кодировка ⁵/₈ выведет дробь ⁵/₈, что будет выглядеть более компактно в текстовом поле.

Для ввода дробей пользователем в формы применяют маски ввода, реализуемые через JavaScript-библиотеки (например, Inputmask). Маска позволяет автоматически ограничивать ввод в формате «число/число» и преобразовывать данные перед отправкой на сервер.

Также рекомендуется обрабатывать ввод дробей на серверной стороне для приведения данных к единому виду. При передаче данных дроби могут кодироваться как обыкновенные дроби (например, 3/4), десятичные числа (например, 0.75) или оставаться в текстовом формате для последующей обработки.

Создание сложных математических дробей через MathML

MathML (Mathematical Markup Language) предоставляет мощные возможности для представления математических формул в веб-документах. Для создания сложных дробей в MathML используется тег <mfrac>, который позволяет делить выражение на числитель и знаменатель. Этот тег идеально подходит для представления как простых, так и более сложных дробей с многоуровневыми выражениями.

Для создания базовой дроби, например, ¹/₂, используется следующий код:

<mfrac>
<mn>1</mn>
<mn>2</mn>
</mfrac>

Этот код создаёт простую дробь 1/2. Однако для более сложных дробей, например, дроби с многоуровневыми выражениями в числителе или знаменателе, можно использовать вложенные теги. Например, для выражения ^(x+1)/_(y+2):

<mfrac>
<mrow>
<mi>x</mi>
<+>
<mn>1</mn>
</mrow>
<mrow>
<mi>y</mi>
<+>
<mn>2</mn>
</mrow>
</mfrac>

Для создания дроби с более сложными операциями, например, ^(a+b)/(c+d), используются аналогичные вложенные теги, что позволяет комбинировать математические операции в числителе и знаменателе. Если выражение содержит степени или другие математические операции, можно применять теги <msup>, <msub> или <mroot> для представления возведений в степень, подстрочных и надстрочных индексов.

Для дроби с корнями, например, ^√(a+b)/_c, код будет следующим:

<mfrac>
<mroot>
<mrow>
<mi>a</mi>
<+>
<mi>b</mi>
</mrow>
<mn>2</mn>
</mroot>
<mi>c</mi>
</mfrac>

Использование MathML для создания дробей помогает сохранять точность отображения и доступность математических формул в веб-приложениях и документах. Этот метод позволяет избежать использования изображений или других решений, которые могут быть не столь гибкими и доступными для пользователей с особыми потребностями.

Особенности отображения дробей в разных браузерах

Отображение дробей в веб-браузерах зависит от поддерживаемых технологий и стандарта рендеринга шрифтов. Разные браузеры могут по-разному интерпретировать HTML и CSS код для дробей, что влияет на их видимость и читаемость. Некоторые браузеры используют встроенные шрифты для отображения математических символов, другие прибегают к различным библиотекам или системным шрифтам.

Основные особенности отображения дробей:

Chrome: Браузер корректно отображает дроби в HTML с использованием стандартных символов Unicode, таких как ¼, ½ и ¾. В некоторых случаях может потребоваться использование CSS для более точной настройки отображения, особенно для сложных дробей. Chrome также поддерживает MathML, что позволяет отобразить дроби в виде форматированного текста, но это может не поддерживаться в старых версиях браузера.
Firefox: Firefox также поддерживает Unicode-дроби, но при использовании MathML могут возникать проблемы с совместимостью. Браузер корректно отображает дроби в стандартном HTML, но для сложных математических выражений могут быть необходимы внешние библиотеки, такие как MathJax, для обеспечения точности отображения.
Safari: В Safari поддержка дробей через Unicode схожа с другими браузерами. Однако стоит отметить, что MathML в Safari не всегда работает должным образом. Для сложных дробей рекомендуется использовать CSS или сторонние библиотеки для правильного отображения.
Edge: Edge использует те же технологии отображения дробей, что и Chrome, и поддерживает Unicode-дроби. В большинстве случаев дроби отображаются корректно, но при работе с более сложными формулами может понадобиться MathML или внешние библиотеки.
Internet Explorer: В старых версиях Internet Explorer возможны проблемы с рендерингом дробей. Браузер ограниченно поддерживает Unicode и может не корректно отображать более сложные математические выражения. В таких случаях рекомендуется использовать изображения или MathML с дополнительной настройкой.

Рекомендации для обеспечения корректного отображения дробей:

Использование символов Unicode для простых дробей (¼, ½, ¾) – это самый универсальный способ, который работает во всех современных браузерах.
Для отображения сложных дробей или математических выражений рекомендуется использовать MathML или сторонние библиотеки, такие как MathJax или KaTeX.
Для более точного контроля отображения дробей можно использовать CSS. Например, для улучшения вертикального выравнивания дробей стоит использовать свойство line-height и настройку font-size для различных элементов дроби.
При поддержке старых версий браузеров (например, Internet Explorer) лучше использовать изображения или отдельные шрифты, специально предназначенные для отображения математических символов.

Для обеспечения лучшего кросс-браузерного отображения рекомендуется тестировать веб-страницу в нескольких браузерах и версиях, чтобы выявить возможные проблемы и применить соответствующие решения.

Вопрос-ответ:

Что такое тема этой статьи и для кого она предназначена?

Тема статьи зависит от ее содержания. Если вы имеете в виду конкретную статью, пожалуйста, уточните, и я смогу дать более точный ответ. Однако, статьи часто пишутся для широкой аудитории и могут охватывать различные области: от науки до культуры, бизнеса или технологий. Важно понимать, что статьи могут быть написаны как для специалистов в какой-то области, так и для людей, не обладающих глубокими знаниями в теме.

Какие аспекты темы в статье кажутся наиболее важными?

Актуальные аспекты темы в статье зависят от ее содержания. Например, если статья посвящена экономике, важными аспектами могут быть влияние экономических факторов на повседневную жизнь людей или изменения в глобальной экономике. Если тема касается экологии, то в центре внимания могут быть проблемы загрязнения окружающей среды или изменения климата. В любом случае, статья обычно фокусируется на наиболее значимых и обсуждаемых вопросах, которые могут иметь последствия для общества или бизнеса.

Как получить больше информации по теме, затронутой в статье?

Чтобы получить более подробную информацию, можно начать с дополнительных источников: книги, научные исследования, интернет-ресурсы и специализированные публикации. Часто статьи ссылаются на другие работы или упоминают исследования, которые можно использовать как отправную точку для углубленного изучения. Также можно искать видео, лекции или интервью с экспертами, которые помогают лучше понять тему.

Какие выводы можно сделать из статьи, и как они могут повлиять на личное или профессиональное поведение?

Выводы из статьи зависят от ее основной идеи. Например, если статья касается улучшения личной эффективности или карьерного роста, то она может предложить конкретные методы для повышения продуктивности, улучшения навыков или изменений в повседневной жизни. В случае более технических тем, выводы могут быть ориентированы на практическое применение технологий или методов для улучшения рабочих процессов. Каждое решение, сделанное на основе статьи, зависит от того, как эти выводы будут соответствовать текущим нуждам читателя.

Почему эта статья может быть полезна для читателей, и как можно использовать полученную информацию?

Статья может быть полезной, если она дает читателю новые идеи или полезную информацию по определенной теме. Например, она может предложить советы по личной эффективности, новые подходы к решению рабочих проблем или анализ актуальных тенденций в той или иной области. Информация, полученная из статьи, может быть использована для улучшения качества жизни или для принятия более обоснованных решений в профессиональной деятельности. Также важно, что знания, полученные из статьи, можно применять на практике, адаптируя их к личным или профессиональным нуждам.