Maple – это мощная среда для символьных и численных вычислений, широко используемая в инженерных, научных и образовательных задачах. Её ядро основано на языке программирования, оптимизированном для работы с математическими выражениями. В отличие от многих других систем, Maple позволяет комбинировать аналитические и численные методы в рамках одного документа, без необходимости переключаться между разными инструментами.
Для начала работы важно освоить интерфейс Maple: область ввода выражений, панель задач и палитры. Ввод формул осуществляется в естественной математической записи, а интерактивные палитры позволяют быстро вставлять интегралы, суммы, производные и другие конструкции без ручного набора. Команды типа int(), diff(), solve(), simplify() используются для выполнения стандартных операций – интегрирования, дифференцирования, решения уравнений и упрощения выражений.
Одна из ключевых возможностей Maple – работа с системами уравнений и матричными выражениями. Команда LinearSolve() решает системы линейных уравнений, а функция Matrix() позволяет задавать и манипулировать матрицами любого размера. Для визуализации данных Maple предлагает инструменты построения 2D- и 3D-графиков через команды plot() и plot3d(), где каждый параметр может быть точно настроен с помощью опций – от цветовой схемы до диапазона значений.
При работе с большими вычислениями важно использовать возможности оптимизации: кеширование результатов, упрощение выражений до выполнения численных операций, а также модульную структуру кода с помощью процедур. Процедуры в Maple создаются с использованием ключевого слова proc и позволяют разбить сложные расчёты на логически завершённые блоки.
Maple также поддерживает экспорт результатов в LaTeX, PDF, HTML и другие форматы, что делает его удобным инструментом для подготовки научных отчётов и публикаций. При необходимости автоматизации задач стоит обратить внимание на пакет DocumentTools, позволяющий создавать интерактивные документы и пользовательские интерфейсы на основе форм и кнопок.
Создание и редактирование математических выражений в Maple
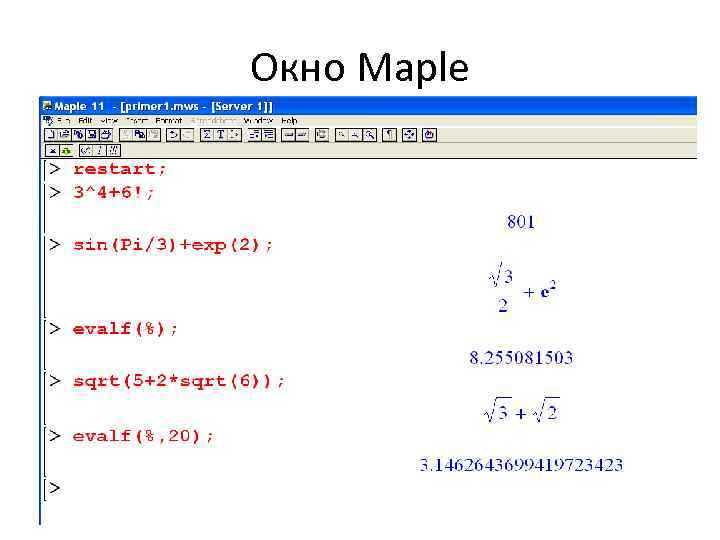
Для ввода математических выражений в Maple предпочтительнее использовать математический режим (Math Mode). Он включается автоматически при наборе в стандартном документе (Document Mode) после ввода математических символов, либо вручную с помощью комбинации клавиш Ctrl+Shift+M.
- Используйте клавишу : для перехода между элементами выражения, например при создании дробей или степеней.
- Чтобы ввести степень, используйте клавишу ^, а для корней – Ctrl+R.
- Ввод интегралов осуществляется через int(), например:
int(sin(x), x). - Для дифференцирования используйте diff(), например:
diff(x^3, x). - Матричные выражения вводятся через
Matrix()или вставляются через меню: Insert → Matrix.
Редактирование выражений возможно как с клавиатуры, так и с использованием контекстного меню:
- Выделите нужную часть выражения – для изменения, замены или удаления.
- Для изменения структуры выражения, например, превращения дроби в произведение, щёлкните правой кнопкой и выберите преобразование (Convert To).
- Вложенные выражения редактируются напрямую: клик по вложенному элементу активирует его редактирование.
- Для форматирования используйте комбинации клавиш: Ctrl+= – ввод уравнения, Ctrl+Space – автозавершение имени функции или переменной.
Maple автоматически интерпретирует введённое выражение. Чтобы уточнить приоритет операций, используйте скобки. Например, (x+1)^2 корректнее, чем x+1^2.
Для отображения выражений в символьной форме используйте команду convert(..., 'inert'), а для редактирования без автоматического упрощения – функцию '%expression' с апострофами.
Решение уравнений и систем уравнений с помощью встроенных функций
В Maple для точного решения алгебраических уравнений применяется функция solve. Она принимает уравнение и переменную, относительно которой выполняется решение. Например, solve(x^3 - 2*x + 1 = 0, x) вернёт все точные корни уравнения. Если корни не выражаются в элементарных функциях, Maple отобразит их в виде RootOf-объектов, с которыми можно выполнять дальнейшие вычисления.
Для численного решения используется функция fsolve. Она полезна, если нужно получить приближённые значения корней. Например, fsolve(sin(x) = x/2, x) вернёт численный корень в десятичном формате. Указание диапазона, например fsolve(sin(x) = x/2, x = 0..2), позволяет найти конкретный корень в заданном интервале.
Системы уравнений решаются передачей списка уравнений и списка переменных. Пример: solve({x + y = 5, x - y = 1}, {x, y}). Maple вернёт единственное точное решение. Если система не имеет аналитического решения, используйте fsolve: fsolve({x^2 + y^2 = 1, x*y = 0.5}, {x, y}).
Уравнения с множеством решений можно анализировать с помощью allvalues, если результат solve содержит RootOf. Например, allvalues(solve(x^5 - x + 1 = 0, x)) вернёт полный список численных корней.
Для проверки найденных решений используйте eval или subs, подставляя корни обратно в уравнение. Это особенно полезно при работе с приближенными результатами fsolve.
Невозможно решить уравнение? Убедитесь, что оно корректно записано, и проверьте, не содержит ли оно уравнений с логическими или дифференциальными компонентами – для них требуются другие инструменты Maple, такие как dsolve или isolve.
Построение графиков и визуализация данных в двумерном и трёхмерном виде
Для построения двумерных графиков в Maple используется функция plot(). Она поддерживает отображение как элементарных функций, так и произвольных наборов точек. Пример: plot(sin(x), x = 0..2*Pi) отрисует синусоиду на заданном интервале. Чтобы отобразить сразу несколько функций, передайте список: plot([sin(x), cos(x)], x = 0..2*Pi).
Для параметрических кривых применяется plot([f(t), g(t), t = a..b]), например: plot([cos(t), sin(t), t = 0..2*Pi]) – окружность. Настроить стиль можно через дополнительные параметры: color = red, thickness = 2, linestyle = dash.
Точки и наборы данных визуализируются функцией pointplot(). Пример: pointplot([[1,2],[2,3],[3,5]]). Для добавления линий между точками используется connect = true.
Трёхмерные графики создаются с помощью plot3d(). Пример: plot3d(sin(x^2 + y^2), x = -2..2, y = -2..2). Для параметрических поверхностей – plot3d([x(u,v), y(u,v), z(u,v)], u = a..b, v = c..d). Функция поддерживает регулировку освещения (lightmodel = light1), цвета и прозрачности (style = surface, transparency = 0.3).
Графики можно комбинировать с помощью display() из пакета plots. Например: with(plots): display([plot1, plot2]). Это удобно для наложения объектов или сравнительного анализа.
Для динамической визуализации применяется animate(). Она позволяет варьировать параметр и наблюдать изменение графика во времени. Пример: animate(plot, [a*sin(x), x = 0..2*Pi], a = 0..2).
Используйте interactive plotting через интерфейс Maple для быстрой настройки без необходимости программирования. Доступ к нему – через меню Plot > Plot Builder.
Использование пакета LinearAlgebra для работы с матрицами и векторами
Для подключения пакета LinearAlgebra в Maple используется команда:
with(LinearAlgebra):
Создание матриц осуществляется функцией Matrix. Пример создания квадратной матрицы 3×3:
A := Matrix([[2, -1, 0], [1, 3, 4], [0, -2, 5]]);
Для создания вектора используется Vector. Одномерный столбец из трёх элементов:
v := Vector([1, 0, -3]);
Умножение матрицы на вектор выполняется стандартным оператором умножения:
u := Multiply(A, v);
Для вычисления определителя используется функция Determinant:
detA := Determinant(A);
Обратную матрицу находят через MatrixInverse, при условии, что определитель не равен нулю:
Ainv := MatrixInverse(A);
Решение системы линейных уравнений в матричной форме Ax = b:
x := LinearSolve(A, b);
Для нахождения собственных значений и векторов применяются функции Eigenvalues и Eigenvectors:
vals := Eigenvalues(A);
vecs := Eigenvectors(A);
Ранг матрицы определяется с помощью Rank:
r := Rank(A);
Транспонирование выполняется через Transpose:
At := Transpose(A);
Для приведения к ступенчатому виду применяется RowEchelonForm:
REF := RowEchelonForm(A);
Использование этих инструментов позволяет выполнять все ключевые операции линейной алгебры в Maple без необходимости ручных вычислений.
Применение Maple для символьного дифференцирования и интегрирования

Для символьного дифференцирования в Maple используется функция diff. Она принимает выражение и переменную, по которой нужно производить дифференцирование. Например, команда diff(sin(x^2), x) возвращает 2*x*cos(x^2). Поддерживается дифференцирование по нескольким переменным: diff(x^2*y^3, x, y) вычислит смешанную производную второго порядка.
Чтобы упростить результат, применяйте функцию simplify: simplify(diff(exp(x)*sin(x), x)) выдаст результат в свернутом виде. Для задания производной как функции используйте D: f := x -> x^2 + 3*x; D(f) создаёт производную функции f.
Символьное интегрирование выполняется с помощью int. Выражение int(x^2*sin(x), x) возвращает первообразную в аналитическом виде. Для определённого интеграла укажите пределы: int(exp(-x^2), x = -infinity .. infinity) вычисляет интеграл Гаусса. Если аналитическое решение невозможно, Maple вернёт результат в виде невычисленного интеграла.
Для контроля над методом интегрирования используйте параметр method, например: int((1+x)^(-1), x, method = 'series'). Это особенно полезно при работе со специальными функциями или разложениями.
Функции diff и int совместимы с выражениями, содержащими параметры и константы. Это позволяет получать общие решения и формулы, пригодные для подстановки численных значений на следующих этапах анализа.
Организация вычислений с использованием пользовательских функций и процедур
В Maple создание пользовательских функций и процедур позволяет структурировать вычисления и повысить повторное использование кода. Для определения функции используется синтаксис вида f := x -> выражение;, где x – входной параметр. Это обеспечивает вычисление значения для заданного аргумента без необходимости повторного переписывания формулы.
Процедуры объявляются с помощью команды proc, например: p := proc(x, y) ... end proc;. В процедурах можно выполнять несколько последовательных действий, использовать локальные переменные и реализовывать сложную логику с управляющими конструкциями (if, for, while).
Для оптимизации вычислений стоит использовать локальные переменные через ключевое слово local, что предотвращает нежелательное влияние на глобальную область видимости. Также при работе с большими массивами данных эффективнее передавать аргументы по ссылке, а не создавать копии.
Рекомендуется разбивать сложные вычисления на набор мелких процедур с чёткой функциональностью. Это облегчает отладку и повторное использование. Maple позволяет вызывать процедуры рекурсивно, что полезно для решения задач с естественной рекурсивной структурой (например, вычисление факториала или чисел Фибоначчи).
Для повышения производительности используйте встроенные функции Maple внутри процедур, поскольку они оптимизированы на уровне ядра системы. При необходимости длительных вычислений процедуру можно дополнить инструкциями по отслеживанию прогресса (print, time).
Сохраняйте пользовательские функции и процедуры в файлах с расширением .mpl для последующего подключения с помощью read. Это упрощает управление большими проектами и совместную работу.
Автоматизация задач с помощью циклов и условных операторов
В Maple циклы и условные операторы позволяют создавать компактные и эффективные алгоритмы для повторяющихся и ветвящихся вычислений. Правильное применение этих конструкций снижает объем ручной работы и минимизирует ошибки.
Основные виды циклов в Maple:
for– выполняет блок кода с заданным числовым диапазоном или по элементам списка/множества.while– повторяет выполнение, пока условие истинно.repeat ... until– выполняет блок минимум один раз и повторяет до выполнения условия.
Типичные задачи автоматизации с использованием циклов и условий:
- Вычисление последовательностей и рядов с проверкой условий сходимости.
- Обработка массивов данных с фильтрацией элементов по заданным критериям.
Рекомендации по применению:
- Для повышения читаемости кода используйте явные условия выхода из циклов и избегайте вложенных циклов при возможности разбиения задачи.
- Используйте
if ... elif ... elseдля чёткой обработки различных ветвлений вместо вложенныхif, что упрощает отладку. - Оптимизируйте циклы, минимизируя количество операций внутри, например, вычисляйте постоянные выражения вне цикла.
- Используйте встроенные функции Maple, например,
mapиselect, для обработки коллекций вместо циклов, когда это возможно.
for n from 1 to 10 do
f := factorial(n);
if (f mod 2) = 0 then
print(f);
end if;
end do;Циклы и условия позволяют интегрировать логику в вычисления, адаптируя алгоритмы к динамическим условиям задачи и значительно сокращая время ручного вмешательства.
Экспорт результатов в различные форматы: PDF, LaTeX, Excel
В Maple экспорт данных и вычислений в нужный формат выполняется через встроенные команды и меню, позволяя сохранить результаты для дальнейшей обработки или публикации.
Для экспорта в PDF используйте команду Export с указанием формата:
Export("путь/к/файлу.pdf", worksheet)
где worksheet – имя листа или объекта для экспорта. Эта команда сохраняет точное визуальное представление документа, включая формулы и графики, без потери качества.
При необходимости экспортировать отдельные выражения или уравнения в LaTeX используйте команду latex(). Например:
latex(expr)
где expr – Maple-выражение. Полученный LaTeX-код можно вставлять в документы, поддерживающие этот язык разметки, сохраняя точность математических формул.
Для создания целых LaTeX-документов существует функция ExportLaTeX(), позволяющая преобразовать Maple-рабочий лист в файл .tex с настройками оформления и подключением необходимых пакетов.
Экспорт в Excel реализован через команду ExportMatrix() или Export() с указанием формата CSV или XLSX. Например:
Export("путь/к/файлу.xlsx", matrix, "xlsx")
где matrix – матричный объект или таблица данных. Для сохранения более сложных таблиц с заголовками и стилями рекомендуется сначала подготовить структуру данных в виде списка списков или DataFrame, затем экспортировать.
При работе с большими объемами данных предпочтительно использовать формат CSV, поскольку он поддерживается любыми табличными редакторами и легче обрабатывается:
Export("путь/к/файлу.csv", data, "csv")
Maple поддерживает автоматическое преобразование и кодировку, но рекомендуется проверять локализацию и кодировку в итоговых файлах, особенно при экспорте в LaTeX и Excel, чтобы избежать проблем с кириллицей.
Вопрос-ответ:
Какие основные типы задач можно решать с помощью Maple?
Maple позволяет выполнять широкий спектр вычислений — от простых арифметических операций до сложного анализа и моделирования. С его помощью удобно решать уравнения, строить графики функций, выполнять символьные преобразования и вычислять интегралы и производные. Кроме того, Maple поддерживает численные методы, что делает программу подходящей для анализа экспериментальных данных и решения инженерных задач.
Как начать работу с интерфейсом Maple новичку?
Для знакомства с Maple стоит сначала освоить основные элементы интерфейса: рабочее пространство, панель инструментов и меню. Важным шагом будет изучение способов ввода математических выражений — можно использовать клавиатуру, меню символов или встроенный редактор. Начните с создания нового документа, попробуйте ввести простое выражение, например, вычислить 2+2, и посмотреть результат. Это поможет понять, как работает система и как вводимые команды отображаются в окне программы.
Какие возможности Maple предоставляет для визуализации данных?
Maple предлагает широкий выбор инструментов для построения графиков и диаграмм. Можно создавать двумерные и трёхмерные графики функций, отображать данные в виде гистограмм, точечных диаграмм и поверхностей. Визуализация позволяет настроить цвет, стиль линий, подписи осей и другие параметры, что помогает лучше анализировать информацию. Кроме того, графики можно анимировать, что удобно для изучения изменения параметров во времени или в зависимости от других переменных.
Как в Maple автоматизировать повторяющиеся вычисления?
Для автоматизации в Maple используют процедуры и скрипты. Можно создавать собственные функции, которые выполняют определённые действия с входными данными. Это позволяет не вводить одинаковые команды вручную многократно, а просто вызвать подготовленную процедуру с нужными параметрами. Также в Maple доступен модуль для написания программ на языке Maple, где можно реализовать циклы, условия и другие конструкции, что значительно облегчает работу с большими объёмами вычислений.
Можно ли в Maple работать с большими массивами данных и как это организовать?
Да, Maple поддерживает работу с матрицами, векторами и списками, что позволяет обрабатывать большие наборы данных. Для удобства существуют специальные команды и функции для создания, изменения и анализа таких структур. Работа с большими массивами часто сопровождается использованием циклов и условных операторов, а также функциями для быстрого доступа к элементам. Важно структурировать данные правильно, чтобы последующая обработка и вычисления проходили максимально гладко.
Как создать и решить уравнение в Maple?
Для создания уравнения в Maple достаточно использовать символ равенства, например, написать y = x^2 + 3. Чтобы решить уравнение, применяется команда `solve`. Например, чтобы найти корни уравнения x^2 — 4 = 0, нужно ввести `solve(x^2 — 4 = 0, x)`. Maple выведет значения x, при которых уравнение выполняется. Можно также решать системы уравнений, перечисляя их в списке внутри команды `solve`.