Как решать дифференциальные уравнения в mathcad

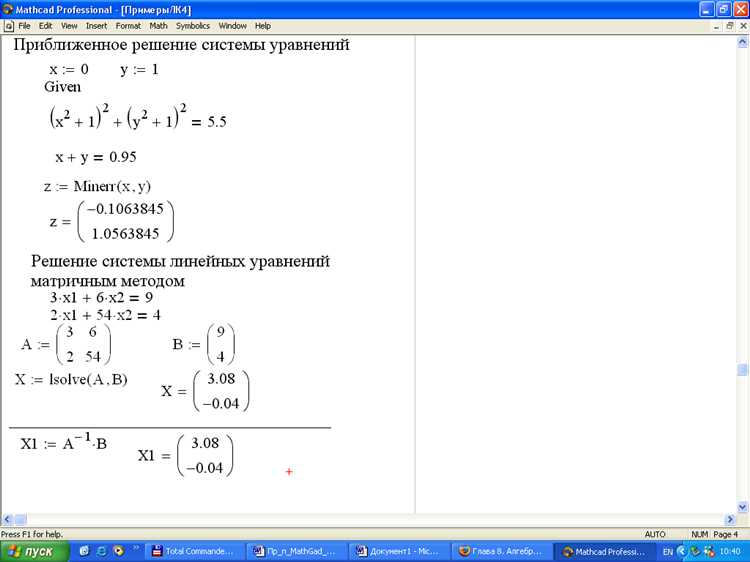
Mathcad предоставляет встроенные численные и символьные методы для решения дифференциальных уравнений первого и более высоких порядков. Благодаря функции Odesolve можно получить численное решение задачи Коши для обыкновенных дифференциальных уравнений (ОДУ) с явным указанием начальных условий и шагом интегрирования.

Для символьного анализа используется оператор solve в сочетании с символьной функцией →, позволяющей получить аналитическое выражение общего или частного решения. При этом система автоматически учитывает характер уравнения и подбирает метод: метод вариации постоянных, интегрирующий множитель или приведение к уравнению с разделяющимися переменными.

Особенность Mathcad – возможность визуального сопровождения процесса решения. Уравнение вводится в естественной математической записи, а результат отображается в удобной форме сразу после ввода. Для систем уравнений применяется векторно-матричный формат, где каждое уравнение оформляется как элемент вектора или столбца.

Параметры численного метода, такие как точность, длина шага и тип алгоритма (например, Рунге-Кутта 4-го порядка), настраиваются вручную, что позволяет контролировать устойчивость и точность результата. Mathcad также позволяет строить графики фазовых портретов и зависимостей решений от времени без необходимости программирования вручную.

Пошаговое задание начальных условий для обыкновенных дифференциальных уравнений

Шаг 1. Объявление независимой переменной

В Mathcad необходимо явно указать переменную времени или независимую переменную, от которой зависит решение. Например, задайте t := 0..10 для интервала расчёта от 0 до 10.

Шаг 2. Определение переменных состояния

Объявите вектор переменных, зависящих от времени. Например, если система второго порядка, используйте: y := vector(2), затем задайте y[0](t) и y[1](t) как функции времени.

Шаг 3. Формулировка уравнения

Используйте оператор Odesolve для указания системы уравнений. Уравнение должно быть представлено в виде выражения производной: y′(t) = f(t, y). Для системы используйте векторную запись производных: y′ := [y[1](t), -y[0](t)].

Шаг 4. Задание начальных условий

Начальные условия задаются как числовые значения переменных на начальной границе интервала. Например, y0 := = 1 и y = 0.

Шаг 5. Решение с использованием Odesolve

Используйте конструкцию: y_sol := Odesolve(t, y, y0). Убедитесь, что имя переменной y, вектор y0 и функция f синтаксически согласованы.

Шаг 6. Визуализация результата

После вычисления y_sol выведите значения y_sol[0](t) и y_sol[1](t) на графике. Используйте функцию plot для построения зависимостей от времени.

Важно: при работе с системой векторных уравнений убедитесь, что размерность начального условия соответствует числу уравнений, а тип переменных строго согласован (функции, числа, векторы).

Использование функции Odesolve для систем уравнений первого порядка

В Mathcad функция Odesolve предназначена для численного решения систем обыкновенных дифференциальных уравнений первого порядка. Основное условие – система должна быть приведена к нормальной форме, то есть все производные выражены явно.

• Для активации Odesolve необходимо создать область решения (solve block), заключённую между операторами Given и функцией Odesolve.
• Внутри блока указываются уравнения системы в виде выражений с производными, например: y'(t) = f(t, y, z), z'(t) = g(t, y, z).
• Начальные условия задаются отдельно: y(t₀) = y₀, z(t₀) = z₀. Все переменные и параметры должны быть определены до начала блока.
• После определения уравнений и условий вызывается Odesolve(t), где t – независимая переменная.

Функция возвращает вектор-функцию, если система включает более одного уравнения. Чтобы получить значения отдельных компонент, используется индексация: Y(t)₀, Y(t)₁ и т.д.

Рекомендуется:

1. Явно указывать диапазон переменной t перед использованием Odesolve, например: t := 0, 0.01 .. 10.
2. Проверять размерность и тип возвращаемого значения с помощью функций last и type, особенно при работе с параметрически заданными правыми частями.
3. Избегать синтаксических неоднозначностей: производные должны быть заданы в виде y'(t), а не через другие обозначения.

Mathcad автоматически использует один из встроенных численных методов (по умолчанию – Radau), но метод можно явно задать через аргумент в скобках: Odesolve(t, method). Доступны методы rkfixed, adams, radau и другие. Выбор метода влияет на точность и скорость решения, особенно при жёстких системах.

Преобразование уравнений высших порядков к системе уравнений первого порядка

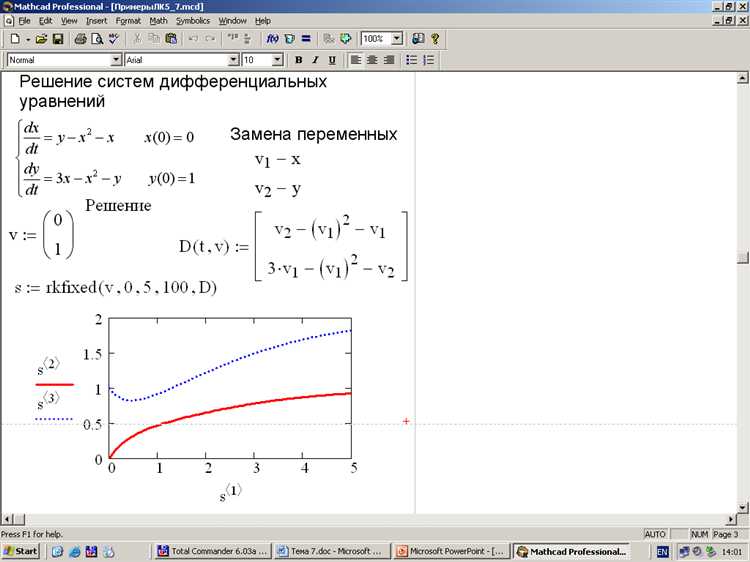
Для численного решения в Mathcad уравнение n-го порядка необходимо переписать в виде системы дифференциальных уравнений первого порядка. Это позволяет применять встроенные решатели, работающие с векторной формой записи.

Рассмотрим пример. Имеется уравнение второго порядка:

y» + 3y’ — 4y = sin(t)

Введём новые переменные: y₁ = y, y₂ = y’. Тогда система примет вид:

y₁’ = y₂

y₂’ = -3y₂ + 4y₁ + sin(t)

В Mathcad необходимо задать вектор-функцию, описывающую правые части системы. Например:

F(t, Y) := [Y₂; -3·Y₂ + 4·Y₁ + sin(t)]

Y := [y₁; y₂]

После этого используется функция Odesolve внутри solve block. В качестве начальных условий указываются значения y₁(0) и y₂(0).

Если порядок уравнения выше второго, количество дополнительных переменных увеличивается. Для третьего порядка: y₁ = y, y₂ = y’, y₃ = y», тогда y₁’ = y₂, y₂’ = y₃, y₃’ = выражение из исходного уравнения.

Все производные выражаются через первые производные новых переменных. Это упрощает настройку решателя и позволяет контролировать поведение каждого компонента решения отдельно.

Настройка параметров численного метода решения в блоке Odesolve

Блок Odesolve в Mathcad поддерживает несколько численных методов решения обыкновенных дифференциальных уравнений. От выбора метода и параметров зависит точность и скорость расчёта.

• Метод: Выбор метода осуществляется в раскрывающемся списке внутри блока. Доступны методы: Adams (по умолчанию), BDF, Radau, Rkf45, Rkfixed. Метод Adams эффективен для нежёстких систем, BDF – для жёстких.
• TOL: Параметр допуска (TOL) определяет относительную погрешность. Чем меньше значение, тем выше точность, но увеличивается время вычислений. Рекомендуется начинать с 1·10^-3 и снижать при необходимости.
• IC: Начальные условия задаются в виде системы. Каждое уравнение должно быть записано явно, например: y(0) = 1, y'(0) = 0.
• Диапазон интегрирования: Указывается в виде: x = 0..10. Увеличение шага может повлиять на устойчивость решения. Mathcad автоматически разбивает интервал, но при необходимости шаг можно ограничить параметрами внутри метода Rkfixed.
• Максимальное число шагов: В параметрах документа через Worksheet Options > Calculation можно установить максимальное число шагов интегрирования. Это помогает отследить зацикливание решения или неустойчивость метода.

Для повышения стабильности при решении жёстких задач предпочтительно использовать Radau или BDF с уменьшенным значением TOL и явно заданными начальными условиями. Использование Rkfixed требует явного задания шага и не адаптирует его по ходу интегрирования.

Построение графиков решения дифференциальных уравнений в Mathcad

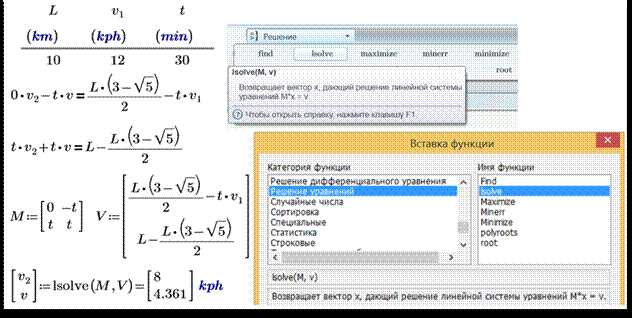
Для визуализации решений дифференциальных уравнений в Mathcad используется функция plot, которая позволяет отображать графики численных решений, полученных, например, с помощью ode или rkfixed. После получения массива значений переменной и соответствующих значений функции, их необходимо передать в аргументы построителя графиков.

Пример: пусть система задана уравнением y' = y - x² + 1 с начальными условиями y(0) = 0.5. Сначала задаётся диапазон переменной x := 0, 0.1 .. 4. Затем вызывается численный решатель: y := rkfixed(f, 0.5, x, 0.1), где f(x, y) := y - x² + 1.

Для построения графика: выберите на рабочем листе вставку графика, затем укажите в осях x и y соответствующие переменные. Mathcad автоматически построит дискретную кривую по рассчитанным точкам.

Чтобы обеспечить корректное отображение, убедитесь, что вектора x и y имеют одинаковую длину. Также рекомендуется явно задавать границы осей, особенно при анализе поведения решений на малых или больших отрезках. Это выполняется через двойной щелчок по графику и редактирование параметров осей.

Для отображения нескольких решений или фазовых траекторий используйте векторную нотацию: plot(x, y₁, y₂, ...). Для систем уравнений удобно строить фазовые портреты, передавая на оси различные переменные, например plot(y₁, y₂).

Если решение имеет жёсткий характер, при построении графика могут появляться скачки или осцилляции. В этом случае необходимо уменьшить шаг интегрирования или использовать решатели, устойчивые к жёсткости, такие как odesolve.

Графики в Mathcad являются динамическими: при изменении параметров решения они автоматически обновляются. Это позволяет оперативно анализировать влияние начальных условий и параметров уравнения на поведение решения.

Обработка ошибок и проверка корректности ввода уравнений

В Mathcad критически важно обеспечить точный ввод дифференциальных уравнений, поскольку любая синтаксическая или логическая ошибка приводит к неверным решениям. Прежде всего, следует использовать встроенный редактор выражений с подсветкой синтаксиса – он автоматически выявляет пропущенные скобки, неправильное использование операторов и ключевых слов.

Для проверки корректности вводимого уравнения рекомендуют выполнять тестовые подстановки: подставлять граничные значения или аналитически известные решения, чтобы убедиться в правильности формулировки. Важно строго соблюдать обозначения переменных и функций, избегая неоднозначностей, которые Mathcad не распознает.

Если решение не сходится или выдается сообщение об ошибке, имеет смысл разделить уравнение на части и проверить каждую отдельно. Использование функции Trace позволяет отследить шаги вычислений и выявить точку сбоя.

Необходимо контролировать размерность всех выражений, особенно при работе с физическими моделями. Mathcad поддерживает единицы измерения, и несоответствие размеров приводит к ошибкам или бессмысленным результатам.

При численном решении уравнений рекомендуется задавать начальные условия и параметры с достаточной точностью, чтобы избежать накопления ошибок. Оптимально использовать встроенные средства проверки сходимости решений и адаптивного шага интегрирования.

В случаях сложных уравнений полезно задействовать функцию отладки, отключая части уравнения и проверяя промежуточные результаты. Это ускоряет локализацию ошибок и предотвращает повторный ввод формул с нуля.

Пример решения задачи с переменными коэффициентами

Рассмотрим дифференциальное уравнение первого порядка с переменными коэффициентами:

y’ + (2x / (1 + x²)) y = sin(x)

Для решения задачи в Mathcad необходимо выполнить следующие шаги:

1. Задайте функцию коэффициента при y:

p(x) := 2x / (1 + x²)

2. Определите правую часть уравнения:

f(x) := sin(x)

3. Укажите начальное условие, например, y(0) = 1:

y(0) = 1

4. Используйте встроенную функцию решения ОДУ – ode. Запишите уравнение в виде выражения для производной:

dy/dx = -p(x) * y + f(x)

5. В Mathcad сформулируйте команду решения, например:

y := ode(y', x, y0, x0..xf)

где y' – выражение для производной, y0 – начальное значение, x0 и xf – границы интервала решения.

После вычисления значения y(x) можно визуализировать результат или вычислить значения в интересующих точках. Такой подход обеспечивает точное численное решение уравнений с переменными коэффициентами без преобразований вручную.

Решение краевых задач для дифференциальных уравнений

В Mathcad реализован функционал, позволяющий эффективно решать краевые задачи для обыкновенных дифференциальных уравнений (ОДУ). Основным инструментом служит функция odesolve, при этом граничные условия задаются явно для каждого конца интервала.

Для постановки краевой задачи необходимо определить уравнение в форме системы первого порядка, если оно задано в высших производных, и определить граничные условия в виде уравнений, связывающих значения функции и её производных на концах интервала.

Например, для задачи вида y» + p(x)y’ + q(x)y = f(x) с условиями y(a) = α и y(b) = β необходимо преобразовать уравнение в систему: y1 = y, y2 = y’, тогда система примет вид:

y1′ = y2

y2′ = f(x) — p(x) y2 — q(x) y1

Граничные условия задаются как y1(a) = α и y1(b) = β. Mathcad позволяет задать их через отдельный вектор, используемый в функции odesolve для численного интегрирования.

При решении задач с краевыми условиями важно выбирать подходящий метод численного решения. В Mathcad применяется метод коллокации или метод прогонки, обеспечивающие устойчивость и точность вычислений. В зависимости от сложности уравнения, рекомендуется задавать начальные приближения, что ускоряет сходимость.

Решение можно визуализировать с помощью встроенных графиков, позволяющих оценить соответствие граничным условиям и корректность результата. При анализе решений важно проверять гладкость функций и соответствие заданным условиям на концах интервала.

Оптимизация вычислительного процесса достигается путём точного задания диапазона переменной и шагов интегрирования, что снижает вычислительную нагрузку без потери точности.

Вопрос-ответ:

Как в Mathcad задавать дифференциальное уравнение для решения?

В Mathcad для определения дифференциального уравнения нужно сначала задать функцию с помощью оператора «:=». Затем через производные указывают уравнение, используя обозначения производных, например, y′ или dy/dx. После этого уравнение можно передать в встроенную функцию решения, например, «ode» или «rkfixed», в зависимости от задачи.

Какие типы дифференциальных уравнений можно решать в Mathcad?

Mathcad поддерживает решение обыкновенных дифференциальных уравнений (ОДУ) различных порядков, как с начальными, так и с краевыми условиями. Можно работать с системами ОДУ, а также с уравнениями в явной или неявной форме. Однако для некоторых сложных видов уравнений, например, с жесткими параметрами, может понадобиться дополнительная настройка параметров метода.

Как задать начальные условия при решении дифференциального уравнения в Mathcad?

Начальные условия в Mathcad прописываются как уравнения, определяющие значения функции и её производных в начальной точке. Обычно это делается в формате y(x0)=y0, где x0 — начальная точка, а y0 — значение функции. Эти условия передаются в функцию решения вместе с самим дифференциальным уравнением, чтобы программа могла правильно вычислить интеграл.

Можно ли визуализировать решение дифференциального уравнения в Mathcad?

Да, Mathcad позволяет строить графики полученных решений. После того как решение вычислено, его можно отобразить с помощью встроенных инструментов графиков, указав переменную по оси X и значение функции по оси Y. Это помогает наглядно оценить поведение решения и проверить корректность вычислений.

Какие основные ошибки возникают при решении дифференциальных уравнений в Mathcad и как их избежать?

Частые ошибки связаны с неправильным заданием уравнения или условий, использованием некорректных обозначений производных, а также с неверным выбором метода решения. Чтобы минимизировать ошибки, важно проверить правильность синтаксиса, уточнить параметры функции и начальные условия, а при сложных задачах внимательно выбирать численный метод и шаг интегрирования.

Как в Mathcad можно задать и решить систему обыкновенных дифференциальных уравнений?

Для решения системы ОДУ в Mathcad необходимо сначала определить уравнения в виде функций с соответствующими начальными условиями. Обычно используется встроенная функция `rkfixed` или `rk` (метод Рунге-Кутты). Нужно задать вектор неизвестных функций и их производных, затем вызвать численный решатель, указав диапазон изменения переменной. Mathcad автоматически вычислит приближенное решение и построит график, если требуется.