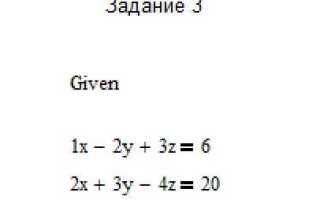Как решать уравнения в mathcad prime

В среде Mathcad Prime решение уравнений не ограничивается лишь вводом формул – здесь реализована визуальная логика, позволяющая комбинировать вычисления, текст и графику в одном документе. Это особенно важно при работе с инженерными и научными задачами, где требуется не только найти численное значение, но и обосновать каждый шаг расчета.

Для начала необходимо определить тип уравнения: алгебраическое, дифференциальное, или система уравнений. В Mathcad Prime алгебраические уравнения решаются с использованием функции solve либо оператора root для численного поиска. При этом важно задать переменные через двоеточие (:=), а сами уравнения – с помощью знака равенства (=), а не присваивания.

Например, чтобы решить уравнение x² — 5x + 6 = 0, необходимо ввести его как выражение x^2 — 5·x + 6 = 0 и использовать команду root(x² — 5·x + 6, x). Для получения обоих корней лучше задать функцию и отобразить график – это обеспечит наглядный выбор начальных приближений для метода Ньютона.

При работе с системами уравнений применяется встроенный оператор solve block, который начинается с ключевого слова Given. Далее последовательно задаются уравнения и переменные для нахождения. Решение системы выполняется через функцию Find. Поддерживается как символьное, так и численное решение, в зависимости от контекста и структуры выражений.

Mathcad Prime позволяет использовать параметры управления точностью, выбирать численные методы решения и визуализировать результаты в виде графиков. Это делает процесс решения уравнений не просто технической задачей, а частью полного математического исследования с возможностью гибкой настройки и проверки результатов.

Настройка единиц измерения перед решением уравнения

В Mathcad Prime работа с единицами измерения интегрирована в вычислительное ядро. Перед решением уравнения необходимо убедиться, что все переменные имеют корректные физические размерности. Это исключает ошибки при автоматических преобразованиях и обеспечивает точность результата.

Для задания единицы используйте символ двойной двоеточия ::. Например, чтобы задать давление P в паскалях, введите P := 5⋅10^5 :: Pa. Mathcad автоматически интерпретирует значение как 500 кПа.

По умолчанию Mathcad Prime использует международную систему СИ. Чтобы изменить систему единиц или задать пользовательские настройки, откройте вкладку Math, затем раздел Units. Здесь доступны опции выбора системы (например, SI, USCS) и способ отображения результатов (автоматически или вручную).

Перед подстановкой значений в уравнение проверьте размерности всех параметров. Mathcad не выполнит расчет, если размерности несовместимы. Например, в уравнении F = m⋅a переменные m и a должны быть заданы в килограммах и метрах в секунду в квадрате соответственно. Несовпадение, например граммы вместо килограммов, приведёт к предупреждению о несогласованных единицах.

Корректная настройка единиц – обязательный этап перед решением уравнений, особенно в инженерных задачах. Это позволяет избежать логических ошибок и обеспечивает физическую достоверность вычислений.

Определение переменных и задание исходных данных

Перед решением уравнений в Mathcad Prime необходимо явно определить все переменные и ввести начальные значения. Это обеспечивает однозначность вычислений и предотвращает ошибки в расчетах.

Именование переменных: Mathcad чувствителен к регистру. Переменные x и X считаются разными. Рекомендуется использовать осмысленные названия: R для сопротивления, T для температуры, v для скорости и т.д.

Присваивание значений: Для задания значения переменной используется символ :=. Пример: m := 5. После присваивания Mathcad автоматически интерпретирует переменную как числовую и подставляет ее значение в вычислениях.

Задание единиц измерения: Mathcad позволяет указывать единицы прямо при вводе значения. Например, L := 2 m задает длину 2 метра. Все вычисления автоматически приводятся к согласованным единицам, что упрощает контроль размерностей.

Использование диапазонов: Для задания диапазона значений используется оператор ... Пример: t := 0, 0.1 .. 10 создает вектор времени от 0 до 10 с шагом 0.1. Это удобно при построении графиков и численном решении дифференциальных уравнений.

Определение начальных условий: Если уравнение требует начальных условий (например, при решении ОДУ), их необходимо задать до вызова решающей функции. Пример: y(0) := 1 устанавливает начальное значение функции y при t = 0.

Инициализация матриц и векторов: Для ввода массива вручную используйте комбинацию клавиш Ctrl+M. Mathcad поддерживает индексацию с единицы по умолчанию, но ее можно изменить в параметрах документа.

Проверка и отладка: После задания переменных желательно вывести их на экран, просто набрав имя переменной, чтобы убедиться в корректности значений и размерностей перед решением уравнения.

Использование функции solve для алгебраических уравнений

Функция solve в Mathcad Prime применяется для поиска корней алгебраических уравнений численным методом. Она используется внутри блока Given совместно с уравнением и указанием переменной, относительно которой требуется найти решение.

Для корректного использования необходимо строгое соблюдение синтаксиса. Сначала создается блок Given, затем записывается уравнение в виде равенства (используется логический знак равенства =, а не знак присваивания :=), после чего вызывается функция solve(variable).

Пример: решить уравнение x² − 5x + 6 = 0.

Given
x^2 - 5·x + 6 = 0
solve(x)

Результат: Mathcad Prime вернёт один из корней уравнения. Чтобы получить оба корня, следует использовать root или polyroots, либо задавать начальное приближение в виде find(x) с предварительным определением диапазона переменных.

Особенности:

solve возвращает только одно решение, ближайшее к начальному приближению (если оно указано).
Для систем алгебраических уравнений необходимо использовать блок Given с несколькими выражениями и функцией solve({x, y, ...}).
Все уравнения должны быть непротиворечивыми и выражаться через одну или несколько переменных.

Рекомендации:

Перед применением solve убедитесь, что уравнение корректно введено и использует логический оператор равенства.
Для сложных уравнений с несколькими корнями используйте график функции для выбора начального приближения.
Избегайте неоднозначных переменных – каждая должна быть либо определена ранее, либо указана в аргументе solve.

Применение функции root для поиска конкретного корня

Функция root(f(x), x, a) в Mathcad Prime позволяет найти такой корень уравнения f(x) = 0, который расположен ближе всего к начальному приближению a. Это особенно полезно, когда уравнение имеет несколько корней, и требуется изолировать один из них.

Для успешного применения необходимо задать:

1. Аналитическое выражение функции f(x) с переменной x.

2. Начальное приближение a, которое должно быть максимально близко к предполагаемому корню.

Пример: пусть необходимо найти положительный корень уравнения sin(x) - x/2 = 0. Если известно, что один из корней находится около x = 1, используйте конструкцию:

root(sin(x) - x/2, x, 1)

Mathcad Prime выполнит численное решение и вернёт корень, ближайший к 1. Если изменить значение a, например на 4, результат будет другим, так как функция имеет несколько корней.

Важно: если начальное приближение выбрано слишком далеко от любого корня или попадает в область разрыва, функция может вернуть ошибку или неверный результат. Используйте график функции для предварительной оценки расположения корней.

Функция root поддерживает только уравнения с одной переменной. Для систем уравнений применяется find.

Рекомендуется комбинировать root с графическим анализом и проверкой результата подстановкой в исходную функцию для оценки точности.

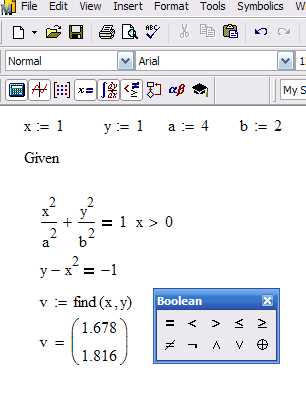
Решение системы нелинейных уравнений с помощью функции given

Для решения системы нелинейных уравнений в Mathcad Prime используется конструкция given совместно с функцией find. Перед использованием необходимо определить переменные и задать уравнения в виде логических выражений с оператором равенства =, а не присваивания :=.

Пример: требуется найти решения системы:

sin(x) + y² = 1

x² + y = 4

Алгоритм:

1. Ввод переменных: нажмите [Ctrl + .] для создания строки программы. Введите: x, y.

2. Установите блок условий: в новой строке введите given.

3. Задайте уравнения в логическом формате:

sin(x) + y² = 1

x² + y = 4

4. Введите функцию find(x, y). Mathcad Prime автоматически выполнит численное решение.

Если необходимо получить результат в определённом диапазоне, задайте начальные приближения через оператор присваивания:

x := 1

y := 1

Mathcad Prime использует итерационный метод, зависящий от начальных значений. При плохом выборе исходных данных возможна ошибка «This variable is undefined» или отсутствие решения. Рекомендуется анализировать поведение системы графически или с помощью подстановки значений, чтобы уточнить область поиска.

При наличии нескольких решений используйте функцию root в выражении:

root(sin(x) + y² — 1, x)

в сочетании с фиксированным y, чтобы поочерёдно находить возможные корни.

Для повышения точности результата регулируйте параметр Tolerance через вкладку Calculation Options, установив, например, 10⁻⁶.

Проверка решения уравнения через подстановку

После нахождения корня уравнения в Mathcad Prime рекомендуется выполнить подстановку решения обратно в исходное выражение. Это подтверждает корректность результата и выявляет возможные ошибки вычислений или ввода.

Для подстановки следует использовать вычисление значения левой и правой части уравнения при найденном корне. В Mathcad Prime создайте переменную, присвоив ей найденный корень, и затем подставьте её в обе части уравнения. Разница между значениями должна стремиться к нулю с учётом допустимой погрешности.

Если при подстановке результат выражения значительно отличается от нуля, проверьте точность вычислений и формат ввода данных. В Mathcad Prime можно увеличить количество знаков после запятой с помощью функций форматирования или изменить настройки точности вычислений.

Для сложных уравнений полезно использовать функцию abs() для оценки модуля разности между левым и правым выражением. Если abs(левая часть — правая часть) < 10^(-6), решение можно считать подтверждённым.

Подстановка также позволяет выявить дополнительные корни, если проверить значения уравнения при других предположениях. Это обеспечивает комплексный контроль и исключает случайные ошибки в процессе решения.

Настройка числового формата и отображения результата

В Mathcad Prime точность и вид отображения числовых значений регулируются через настройки формата результата. Это важно для корректной интерпретации данных и удобства дальнейших вычислений.

Выбор количества знаков после запятой:
- Щёлкните правой кнопкой по числовому результату или по ячейке с вычислением.
- В контекстном меню выберите пункт «Формат числа» (Number Format).
Использование научного формата:
- В диалоге формата можно переключиться на экспоненциальное представление.
- Укажите, сколько знаков после запятой должно отображаться в экспоненциальной записи.
- Рекомендуется для очень больших или очень малых чисел, чтобы избежать длинных числовых строк.

Настройте отображение с использованием алгебраической формы (a + bi) или полярной (r ∠ θ).
Выбор зависит от удобства восприятия и специфики задачи.

Единицы измерения и их отображение:
- Если требуется, отключите автоматическое сокращение единиц для точного контроля над результатом.
Настройка локализации и разделителей:
- Измените разделитель целой и дробной части (точка или запятая) в настройках программы под региональные стандарты.
- Настройте отображение разделителей тысяч, если необходимо, для удобства чтения больших чисел.
Автоматическое обновление формата:
- Включите или отключите функцию автоматического выбора формата в зависимости от величины результата.
- При отключении формат остаётся фиксированным, что полезно при отчётности и стандартизации данных.

Вопрос-ответ:

Как в Mathcad Prime пошагово решить простое алгебраическое уравнение?

Для решения алгебраического уравнения в Mathcad Prime сначала необходимо записать уравнение в рабочей области, например, x^2 — 4 = 0. Далее нужно использовать встроенную функцию решения уравнений, например, solve или root. Вводится команда, которая указывает переменную и уравнение. После этого программа автоматически находит корни. Важный момент — убедиться, что синтаксис команды соответствует требованиям Mathcad Prime. Также можно настроить шаги решения вручную, чтобы видеть промежуточные вычисления и проверять правильность каждого этапа.

Можно ли в Mathcad Prime решать системы уравнений с несколькими переменными, и как это сделать?

Да, Mathcad Prime позволяет решать системы уравнений с несколькими неизвестными. Для этого нужно задать каждое уравнение системы, например, f1(x,y) = 0 и f2(x,y) = 0. Затем используется функция решения систем, где переменные перечисляются через запятую. Обычно применяется команда solve или root с набором уравнений и вектором переменных. Результатом будет набор значений для каждой переменной, который удовлетворяет всем уравнениям системы. Важным моментом является правильное оформление уравнений и выбор начальных приближений для численного метода, если он применяется.

Как в Mathcad Prime настроить отображение промежуточных шагов решения уравнения?

Чтобы видеть промежуточные шаги, можно разбить решение на отдельные вычисления и записать их в отдельных блоках или строках. Например, сначала вычисляется выражение под корнем, затем результат подставляется в основное уравнение. Mathcad Prime поддерживает последовательное вычисление и позволяет вывести значения каждой переменной на отдельной строке. Кроме того, можно использовать комментарии, чтобы пояснять логику каждого шага. Однако встроенной функции автоматического показа каждого промежуточного шага нет, поэтому пользователю нужно организовать это самостоятельно, записывая вычисления последовательно.

Какие ошибки часто возникают при решении уравнений в Mathcad Prime, и как их избежать?

Основные ошибки связаны с неправильным синтаксисом при вводе уравнений и команд решения. Часто встречается забывание знака равенства или неправильное обозначение переменных. Также может возникнуть ошибка, если уравнение не записано в явном виде, то есть переменная не выделена с одной стороны. Для решения систем численно важно задать корректные начальные приближения, иначе программа может не найти решение. Еще одна распространенная ошибка — использование функций вне их области определения, например, извлечение корня из отрицательного числа без комплексных чисел. Чтобы избежать ошибок, стоит внимательно проверять ввод, тестировать уравнение на простых примерах и следить за подсказками программы.

Можно ли в Mathcad Prime решать дифференциальные уравнения и как это реализовать шаг за шагом?

Да, Mathcad Prime предоставляет возможность решения дифференциальных уравнений. Для этого сначала необходимо задать уравнение с производной, например, dy/dx = f(x,y), и начальные условия. Далее применяется встроенный численный метод, такой как Runge-Kutta, через функцию ode или аналогичную. В процессе решения указывается диапазон переменной и начальное значение функции. Чтобы понять ход вычислений, можно выводить результаты на каждом шаге решения или строить график функции. Это позволяет анализировать динамику решения и корректировать параметры при необходимости. Такой подход упрощает работу с дифференциальными уравнениями, делая их решение наглядным.

Как в Mathcad Prime пошагово решить простое алгебраическое уравнение?

Для решения уравнения в Mathcad Prime сначала нужно записать уравнение с использованием математического редактора. Например, для уравнения вида \(x^2 — 4 = 0\) нужно ввести его в рабочую область. Затем необходимо задать переменную, которую требуется найти. После этого следует воспользоваться инструментом решения уравнений — для этого пишется выражение с функцией solve или используется встроенный помощник. Важным шагом является выделение переменной, относительно которой происходит решение. В результате Mathcad покажет значение переменной, которое удовлетворяет уравнению. Такой подход позволяет видеть, как система обрабатывает уравнение по шагам.