Как разложить функцию в ряд фурье в mathcad

Ряд Фурье позволяет представить периодическую функцию в виде суммы синусоидальных компонентов с разными частотами. Mathcad предлагает удобные инструменты для вычисления коэффициентов ряда и построения графиков, что упрощает анализ сложных функций.

В статье подробно рассмотрен алгоритм разложения функции в ряд Фурье на конкретном примере с использованием встроенных возможностей Mathcad. Представлены точные формулы для расчёта коэффициентов a₀, aₙ, bₙ, а также методы численного интегрирования при отсутствии аналитического выражения интеграла.

Каждый этап сопровождается практическими рекомендациями по настройке параметров Mathcad, выбору интервала и количества гармоник для оптимального баланса между точностью и вычислительной нагрузкой. Итоговые графики иллюстрируют качество аппроксимации и влияние числа гармоник на форму ряда.

Подготовка функции к разложению: ввод и проверка в Mathcad

Для корректного разложения функции в ряд Фурье в Mathcad необходимо четко определить выражение и диапазон переменной. Введите функцию с использованием стандартных операторов Mathcad, избегая лишних скобок и нестандартных символов. Например, для функции \( f(x) = \sin(x) + 0.5 \cos(2x) \) введите строку: f(x) := sin(x) + 0.5*cos(2*x).

Проверьте синтаксис, выполнив вычисление значения функции при конкретном x, например, f(0). Если результат отсутствует или выдается ошибка, исправьте формат записи, учитывая чувствительность Mathcad к пробелам и символам.

Установите область определения переменной. Для ряда Фурье обычно выбирается периодическая область, например, от \(-\pi\) до \(\pi\). Задайте диапазон: x := -π..π. Mathcad автоматически распознает диапазон и позволит строить графики и вычислять интегралы на этом интервале.

Проверьте непрерывность функции в выбранном интервале, используя графический инструмент Mathcad. Постройте график plot(x, f(x)) и убедитесь в отсутствии разрывов, исключающих корректное разложение в ряд.

При необходимости используйте команды для численной проверки значений функции в узлах разбиения, чтобы выявить возможные особенности или точки разрыва. Это особенно важно при разложении кусочно-заданных функций.

Настройка периода и области определения для ряда Фурье

Для корректного разложения функции в ряд Фурье в Mathcad необходимо задать период и область определения, соответствующие особенностям исходной функции. Период ряда Фурье определяется длиной интервала, на котором функция рассматривается как периодическая. В Mathcad задайте этот параметр через переменную T, например, T := 2*π для функций с классическим периодом 2π.

Область определения функции в Mathcad ограничивается интервалом [-T/2, T/2] или [0, T]. Выбор зависит от удобства и типа исходной задачи. Для разложения функции, заданной на конечном интервале, рекомендуют расширять её на весь период, обеспечивая периодическое повторение без разрывов.

При использовании встроенных операторов и функций Mathcad для ряда Фурье убедитесь, что аргументы функции и переменные интегрирования корректно связаны с заданным периодом. Для численного интегрирования на периоде укажите границы в точности соответствующие периоду T. Например, для коэффициентов Фурье aₙ и bₙ интегрируйте по переменной x от -T/2 до T/2.

Если функция определена на нестандартном интервале, например, [a, b], для разложения её необходимо сначала привести к периоду T = b — a. При этом переменную внутри Mathcad можно сдвинуть: f(x) → f(x + (a + b)/2), чтобы обеспечить симметрию относительно нуля или начать период с нуля.

Рекомендуется проверить график функции на выбранном интервале, чтобы убедиться в отсутствии скачков или разрывов, которые могут привести к медленной сходимости ряда. При необходимости используйте дополнительное сглаживание или изменение области определения для улучшения результата разложения.

Вычисление коэффициентов a0, an и bn вручную в Mathcad

Для вычисления коэффициентов ряда Фурье вручную в Mathcad необходимо задать исходную функцию и период. Начните с определения периода T и полуинтервала L = T/2.

Коэффициент a0 вычисляется по формуле:

a₀ = (1 / L) * ∫[−L..L] f(x) dx

В Mathcad используйте оператор интегрирования integral или встроенную функцию int, например:

a0 := (1 / L) * int(f(x), x, -L, L)

Для коэффициентов an формула:

aₙ = (1 / L) * ∫[−L..L] f(x) * cos(nπx / L) dx

В Mathcad объявите переменную n как целое число, затем вычислите an:

an(n) := (1 / L) * int(f(x) * cos(n * π * x / L), x, -L, L)

Коэффициенты bn определяются аналогично:

bₙ = (1 / L) * ∫[−L..L] f(x) * sin(nπx / L) dx

Для вычисления в Mathcad:

bn(n) := (1 / L) * int(f(x) * sin(n * π * x / L), x, -L, L)

Рекомендуется задать функцию f(x) через выражение или численный массив, если функция задана дискретно. Обратите внимание, что при численном интегрировании лучше использовать встроенные методы с достаточной точностью, например, quadrature. Для упрощения расчётов можно вычислять коэффициенты на нескольких значениях n с помощью цикла или векторных операций.

Если функция нечётная или чётная, следует учитывать свойства коэффициентов: для чётной f(x) bn = 0, для нечётной an = 0, что позволяет оптимизировать вычисления.

Использование встроенных интегралов Mathcad для нахождения коэффициентов

Для вычисления коэффициентов ряда Фурье в Mathcad применяются встроенные операторы интегрирования, что значительно ускоряет процесс и повышает точность расчетов. Основные коэффициенты a₀, aₙ и bₙ задаются через определенные интегралы функции на промежутке периодичности.

Формулы коэффициентов выглядят так:

a₀ = (1/T) ∫[0..T] f(t) dt,

aₙ = (2/T) ∫[0..T] f(t) cos(2πn t / T) dt,

bₙ = (2/T) ∫[0..T] f(t) sin(2πn t / T) dt,

где T – период функции, n – номер гармоники.

В Mathcad интегрирование реализуется с помощью встроенной функции интеграла, обозначаемой как ∫ или integral(). Для точности лучше задавать пределы интегрирования в виде конкретных чисел, а не символов, что исключает неоднозначности при вычислении.

Пример вычисления коэффициента aₙ в Mathcad:

a_n := (2/T) * ∫(f(t) * cos(2 * π * n * t / T), t, 0, T)

В выражении обязательно указывайте переменную интегрирования и её пределы, чтобы Mathcad корректно интерпретировал оператор.

При использовании встроенного интеграла рекомендуется:

• определять функцию f(t) как выражение или задание переменной,
• фиксировать период T числовым значением,
• использовать именованные переменные для гармоник n, что позволяет легко строить последовательность коэффициентов,
• для повышения точности можно задавать числовую точность в настройках Mathcad.

Для многократных вычислений коэффициентов полезно создавать динамические диапазоны переменных и автоматизировать расчеты с помощью функций или матриц, используя циклы по n. Это избавляет от ручного ввода каждого интеграла.

Формирование ряда Фурье и его запись в Mathcad

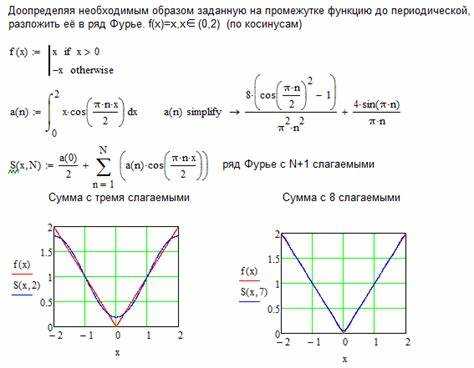
Для построения ряда Фурье в Mathcad необходимо последовательно определить базовые элементы и организовать вычисления с использованием встроенных функций и операторов. Алгоритм следующий:

1. Задайте функцию f(x), которую требуется разложить. Введите её явно или через математическое выражение.
2. Определите период T и полуинтервал L = T/2. Это важно для корректного вычисления коэффициентов.
3. Создайте переменную для индекса n, обозначающего номер гармоники, и задайте диапазон для построения ряда (например, n от 0 до N).
4. Вычислите коэффициенты ряда Фурье:
   • Константный коэффициент: a₀ = (1/L) * ∫[−L..L] f(x) dx
   • Косинусные коэффициенты: aₙ = (1/L) * ∫[−L..L] f(x) * cos(nπx/L) dx
   • Синусные коэффициенты: bₙ = (1/L) * ∫[−L..L] f(x) * sin(nπx/L) dx
5. В Mathcad используйте встроенную функцию int() для вычисления определённых интегралов с указанными пределами.
6. Сформируйте выражение для ряда Фурье:

   S(x) := a₀/2 + Σ (aₙ * cos(nπx/L) + bₙ * sin(nπx/L)), где сумма берётся по n от 1 до N.

7. Реализуйте суммирование через оператор sum() или с помощью цикла for, если требуется более явное управление вычислениями.
8. Проверьте корректность: сравните исходную функцию f(x) и сумму ряда S(x) на нескольких значениях x.

Рекомендуется сохранять каждый вычисляемый коэффициент в отдельную переменную для отладки и последующего анализа. Mathcad автоматически обновляет вычисления при изменении параметров, что упрощает корректировку точности ряда, увеличивая число гармоник N.

Графическое построение исходной функции и ряда Фурье для сравнения

В Mathcad визуализация исходной функции и её приближения рядом Фурье помогает оценить точность разложения. Для этого необходимо построить графики на одном интервале с одинаковой дискретизацией.

1. Задайте диапазон аргумента. Например, для периодической функции с периодом T используйте интервал от 0 до T с шагом не более T/100:
   • x := 0, T/100 .. T
2. Определите исходную функцию f(x) в виде выражения или массива значений по x.
3. Вычислите сумму ряда Фурье с нужным числом членов N:
   • Вычислите коэффициенты a0, an, bn для n = 1..N.
   • Рассчитайте приближение ряда Фурье в каждой точке x:
     
     F_N(x) := a0/2 + Σ (an*cos(2πnx/T) + bn*sin(2πnx/T))
4. Постройте графики исходной функции и ряда Фурье на одном поле:
   • Используйте команду построения графика, добавляя две кривые f(x) и F_N(x).
   • Задайте легенду для удобства сравнения, например: «Исходная функция» и «Ряд Фурье, N=10».
5. Обратите внимание на следующие моменты:
   • Выбор N влияет на точность: увеличение числа членов улучшает совпадение с исходной функцией, но повышает вычислительную нагрузку.
   • Особенно важна плотность точек x – слишком редкий шаг скроет мелкие детали разложения.
   • Для функций с разрывами наблюдается эффект Гиббса; визуализация поможет определить зону и амплитуду колебаний.

Такой подход позволяет наглядно увидеть соответствие ряда Фурье исходной функции и оценить качество аппроксимации в Mathcad.

Анализ сходимости ряда и точности приближения в Mathcad

Для оценки сходимости ряда Фурье в Mathcad используйте построение графиков частичных сумм. Вычислите сумму ряда с увеличением числа членов и визуализируйте поведение функции на выбранном интервале. Оценка ошибки сводится к вычислению разницы между исходной функцией и частичной суммой ряда в контрольных точках.

В Mathcad создайте вектор значений функции и соответствующий вектор значений частичных сумм с шагом по числу членов. Используйте функцию abs для вычисления абсолютной ошибки. Значение максимальной ошибки можно найти через оператор max. Если максимальная ошибка не убывает при добавлении новых членов, это сигнал о недостаточной сходимости.

Для функций с разрывами применяйте сглаживающие фильтры или увеличивайте количество членов ряда, контролируя при этом эффект Гиббса. В Mathcad рекомендуется строить график ошибки в зависимости от номера члена ряда, чтобы визуально определить оптимальное число слагаемых.

Для ускорения сходимости используйте модификации коэффициентов Фурье, например, применяйте окна (окно Кайзера или Хэмминга), реализуемые через массивы весов, перемножаемые на коэффициенты перед суммированием. Mathcad позволяет легко реализовать этот подход через пользовательские функции и циклы.

Автоматизация процесса с помощью пользовательских функций и шаблонов

Для ускорения разложения функции в ряд Фурье в Mathcad целесообразно создать пользовательские функции, которые автоматически вычисляют коэффициенты и строят графики. Основная задача – избежать ручного повторения однотипных вычислений при изменении исходной функции или параметров.

Первым шагом создайте функцию для вычисления коэффициентов a₀, aₙ и bₙ по формулам ряда Фурье, используя встроенные численные интегралы Mathcad. Например, функцию FourierCoefficients(f, L, n), где f – исходная функция, L – полупериод, а n – номер гармоники. Внутри функции используйте оператор интегрирования ∫ с границами от -L до L и формулы для коэффициентов:

a₀ = (1/(2L)) * ∫[−L..L] f(x) dx,
aₙ = (1/L) * ∫[−L..L] f(x) cos(nπx/L) dx,
bₙ = (1/L) * ∫[−L..L] f(x) sin(nπx/L) dx.

Для численной интеграции используйте функцию int с достаточной точностью, задав количество узлов сетки вручную, чтобы избежать ошибок округления при вычислениях.

Далее создайте функцию для построения частичной суммы ряда Фурье: FourierSum(f, L, N, x), где N – число учитываемых гармоник, x – аргумент. Функция должна вызывать FourierCoefficients для всех n=0..N и возвращать сумму вида:

S_N(x) = a₀ + Σ (aₙ cos(nπx/L) + bₙ sin(nπx/L)), n=1..N.

Для упрощения многократного использования создайте шаблон документа Mathcad с предварительно настроенными параметрами: областью интегрирования, пользовательскими функциями, графиками. Это позволит при изменении функции или параметров быстро получить результат, подставляя новые данные без повторного создания вычислительной части.

Рекомендуется сохранять шаблон с понятными именами функций и переменных, а также комментариями для каждой ключевой части кода. Такой подход уменьшит количество ошибок и упростит сопровождение проекта.

Вопрос-ответ:

Как в Mathcad задать функцию для разложения в ряд Фурье?

Для начала в Mathcad нужно ввести функцию, которую планируется разложить. Обычно это делается с помощью определения переменной и выражения, например, f(x) := sin(x) + x^2. Важно задать область определения функции и установить период, если функция периодическая. Затем можно перейти к вычислению коэффициентов ряда Фурье по формулам, используя интегралы на одном периоде.

Какие шаги необходимы для вычисления коэффициентов ряда Фурье в Mathcad?

Сначала определяют период функции и формулы для коэффициентов a0, an и bn. Далее с помощью встроенного оператора интеграла вычисляют интегралы, которые представляют собой средние значения функции, умноженной на синус или косинус. В Mathcad интеграл задаётся с пределами одного периода, например, от -π до π. После вычисления интегралов значения подставляются в формулы для коэффициентов.

Как проверить корректность разложения функции в ряд Фурье в Mathcad?

После вычисления коэффициентов стоит построить график частичной суммы ряда с несколькими членами и сравнить его с графиком исходной функции. В Mathcad можно построить оба графика на одном поле, чтобы визуально оценить совпадение. Чем больше членов ряда включено, тем точнее приближение. Если разложение выполнено правильно, графики должны практически совпадать на заданном интервале.

Можно ли разложить в ряд Фурье функции с разрывами в Mathcad и как это влияет на результат?

Разложение функций с разрывами возможно, однако в окрестности точек разрыва появится эффект Гиббса — колебания и локальные отклонения от исходной функции. В Mathcad это проявляется на графике частичных сумм. Для таких функций ряд Фурье сходится к среднему значению слева и справа от разрыва, поэтому стоит учитывать особенности поведения функции при интерпретации результата.

Как в Mathcad реализовать автоматический расчёт и визуализацию ряда Фурье с увеличением числа членов?

Для этого создают параметр N — количество членов ряда, а затем с помощью циклов или выражений векторного типа вычисляют коэффициенты для каждого n от 1 до N. После этого формируют сумму членов ряда, используя вычисленные коэффициенты и синусы или косинусы. В Mathcad график можно обновлять автоматически при изменении N, что позволяет видеть улучшение аппроксимации функции по мере увеличения количества членов.

Как в Mathcad задать функцию для разложения в ряд Фурье и получить её коэффициенты?

Для начала в Mathcad нужно определить функцию на интервале, для которого будет строиться ряд Фурье. Обычно это периодическая функция, заданная явно или через выражение. После этого с помощью встроенных инструментов или вручную формулируется интеграл для вычисления коэффициентов a₀, aₙ и bₙ. В Mathcad интегралы задаются через оператор интегрирования, который позволяет численно вычислить значения. Далее полученные коэффициенты подставляют в формулу ряда Фурье. В статье пошагово показано, как реализовать каждое из этих действий с использованием конкретных команд и примеров.

Можно ли в Mathcad построить график исходной функции и её аппроксимации рядом Фурье для сравнения?

Да, Mathcad предоставляет удобные средства для визуализации. После вычисления коэффициентов ряда Фурье можно сформировать приближённую функцию, представляющую сумму конечного числа слагаемых ряда. Затем обе функции — исходную и аппроксимирующую — отображают на одном графике. Это позволяет оценить точность приближения и увидеть особенности поведения ряда при разном числе слагаемых. В статье подробно показано, как задать функцию аппроксимации, настроить параметры графика и добиться наглядного сравнения.