Как решать системы уравнений в mathcad

Mathcad предоставляет возможность решать системы линейных и нелинейных уравнений с числовыми или символьными переменными, минимизируя ручные вычисления и ошибки. Программа автоматически подставляет значения, производит численное или символьное решение и визуализирует результаты. Работа с системой начинается с четкой формализации уравнений в виде векторных выражений или функции-системы.

Для численного решения линейной системы вида Ax = b, где A – матрица коэффициентов, x – вектор неизвестных, а b – вектор правых частей, используется встроенная функция lsolve(A, b). Перед вызовом функции необходимо задать все переменные, включая размерность матрицы. Mathcad автоматически проверяет корректность размерностей и возвращает вектор-решение.

Если система содержит нелинейные уравнения, применяют оператор solve block, где переменные объявляются через guess values – приближенные начальные значения. Далее с помощью оператора find() программа итеративно подбирает решение. Для достижения точности важен разумный выбор начальных приближений и корректная настройка единиц измерения, если они применяются.

Важной особенностью Mathcad является возможность визуального отслеживания промежуточных шагов. После построения системы, пользователь может моментально видеть графическую интерпретацию решения или отклонений, особенно при использовании функции root() для поиска пересечений кривых. Это удобно при работе с уравнениями, содержащими параметры или зависимостями от внешних переменных.

Как задать систему алгебраических уравнений в Mathcad

Для ввода системы алгебраических уравнений в Mathcad необходимо использовать операторы определения и встроенную функцию решателя. Уравнения вводятся в виде выражений, приравненных к нулю. Пример: x + y = 10 и x - y = 2. В Mathcad символ равенства для уравнения – =, а не :=, который используется для присваивания значений.

Сначала задаются переменные, участвующие в уравнениях. Они не требуют предварительного определения, но должны быть обозначены как переменные. Далее вводятся сами уравнения в математическом формате. Все выражения должны быть введены в одной области или объединены с помощью клавиши [Ctrl]+[Shift]+[] для создания векторной структуры.

Чтобы передать систему уравнений в решатель, создается вектор уравнений. Для этого используется оператор вектора: нажмите [Ctrl]+[Shift]+[,] и последовательно вводите уравнения в каждую строку. Затем создается вектор переменных, которые необходимо найти, аналогично – с помощью векторного ввода.

Для решения системы применяется функция solve или root из блока Symbolics или Numeric соответственно. В случае численного решения используется функция find(x, y), где x и y – переменные, включённые в вектор. Уравнения передаются в функцию через имя векторной переменной.

Обязательно задать начальные приближения для всех переменных перед использованием find. Это делается с помощью оператора :=, например: x := 1, y := 1. Без этого решатель не запустится.

Все переменные и уравнения должны быть оформлены в одном блоке, иначе Mathcad не сможет распознать систему как целостную. Проверяйте правильность ввода: уравнения должны быть алгебраическими, без неразрешённых символов и синтаксических ошибок.

Настройка области решения с помощью функции solve

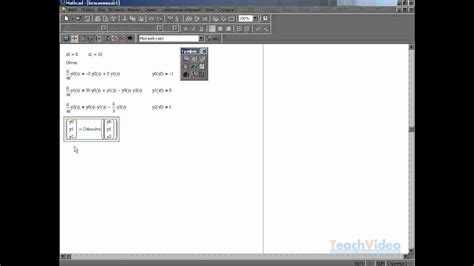
Функция solve в Mathcad используется внутри блока «Given–Find» для численного решения систем нелинейных уравнений. Чтобы корректно настроить область решения, необходимо явно задать начальные приближения для всех переменных системы. Это достигается с помощью выражений вида x := 1, размещённых до оператора Given.

Каждое уравнение должно быть записано с использованием логического равенства = вместо знака присваивания :=. После оператора Given перечисляются все уравнения, относящиеся к системе. Завершает блок вызов solve с аргументами – переменными, подлежащими определению. Порядок переменных имеет значение, так как Mathcad использует его при инициализации итерационного процесса.

Важно обеспечить согласованность размерностей всех выражений. Если хотя бы одно уравнение содержит несогласованные единицы измерения, функция solve выдаст ошибку. При необходимости используйте безразмерные переменные или приводите все величины к одной системе единиц до вычислений.

Для улучшения сходимости указывайте приближения, максимально приближённые к предполагаемым решениям. Если начальные значения далеки от корней, возможна дивергенция метода или поиск ложного решения. Для сложных систем используйте графический анализ или предварительное упрощение модели.

Если система не имеет решений, solve вернёт ошибку “No solution was found”. При этом стоит проверить как корректность уравнений, так и диапазоны возможных значений переменных. Использование функции minerr вместо solve в таких случаях может дать приближённое решение при минимальной ошибке.

Использование оператора Given для задания условий

Оператор Given в Mathcad применяется для явного указания системы уравнений и условий, подлежащих решению. Он необходим при использовании функций find() и minerr(), которые выполняют численное решение.

Для использования Given введите его отдельно перед набором уравнений. После оператора перечисляются все условия, которым должны удовлетворять переменные. Каждое условие вводится как отдельное выражение. Рекомендуется использовать уравнения в форме равенств (=), а не присваиваний (:=).

Пример:

Given
x + y = 10
x - y = 2

Чтобы найти значения переменных, введите выражение:

find(x, y)

Результатом будет численное решение: x = 6, y = 4.

При наличии нелинейных уравнений или систем с условиями неравенств также можно использовать Given. Неравенства (например, x > 0) вводятся как отдельные строки после Given. Однако в этом случае следует применять minerr(), так как find() не обрабатывает неравенства напрямую.

Важно: переменные должны быть предварительно не определены с помощью :=, иначе Mathcad интерпретирует их как известные значения. Все вводимые уравнения должны иметь одинаковую размерность либо быть безразмерными, иначе система выдаст ошибку единиц измерения.

При решении более сложных задач можно использовать вектора и матрицы в условиях после Given. Это позволяет задавать системы с большим числом переменных в компактной форме и решать их эффективно.

Определение начальных приближений при численном решении

Выбирать начальные приближения необходимо на основе анализа графиков функций, входящих в систему. Постройте графики каждого уравнения и определите области возможных пересечений. Эти точки пересечения служат ориентиром для выбора значений переменных, близких к предполагаемому решению.

Если аналитическое построение невозможно, используйте численные методы поиска корней отдельных уравнений системы. Например, при наличии функции двух переменных f(x, y), можно зафиксировать y и найти корни f(x, y) = 0 относительно x. Повторив для нескольких значений y, получите начальные пары (x, y), пригодные для старта.

В Mathcad удобно задавать начальные приближения в виде вектора. Например, при решении системы из двух уравнений используйте: guess := [x₀, y₀]. Значения x₀ и y₀ выбирайте из окрестности предполагаемого корня. Рекомендуется проверять чувствительность результата к изменению guess, чтобы убедиться в устойчивости метода.

Для жестких или плохо обусловленных систем полезно предварительное масштабирование переменных. Приведите переменные к безразмерной форме, чтобы избежать перекоса в масштабах и ускорить сходимость.

Начальные приближения должны удовлетворять условиям области определения всех функций в системе. Mathcad не проверяет это автоматически, поэтому необходимо исключить деление на ноль, логарифмы от отрицательных чисел и другие сингулярности.

Работа с символическим решением систем уравнений

Mathcad позволяет решать системы уравнений не только численно, но и в символьной форме, что особенно полезно для аналитического анализа. Для этого используется оператор solve внутри команды symbolic (символическое равенство обозначается знаком := и применяется вместе с командой solve).

1. Вводите уравнения с использованием оператора равенства =, а не присваивания :=. Например, x + y = 3, x - y = 1.
2. Обозначьте систему уравнений в виде вектора: eqs := [x + y = 3, x - y = 1].
3. Задайте вектор переменных: vars := [x, y].
4. Примените символическую команду: solve(eqs, vars) →. Mathcad вернёт точное аналитическое решение.

При необходимости упростить результат используйте команду simplify:

• simplify(solve(eqs, vars)) → упрощает выражения в решении.

Для подстановки значений используйте subs:

• subs(x=2, y=1, expr) подставит значения в выражение или систему.

Если система содержит параметры, Mathcad выведет решение в параметрическом виде. Используйте assume для задания ограничений:

• assume, a ≠ 0 перед решением исключит деление на ноль в выражении с параметром a.

Символическое решение позволяет исследовать поведение системы при разных значениях параметров без необходимости повторного численного решения.

Анализ результатов и проверка полученных решений

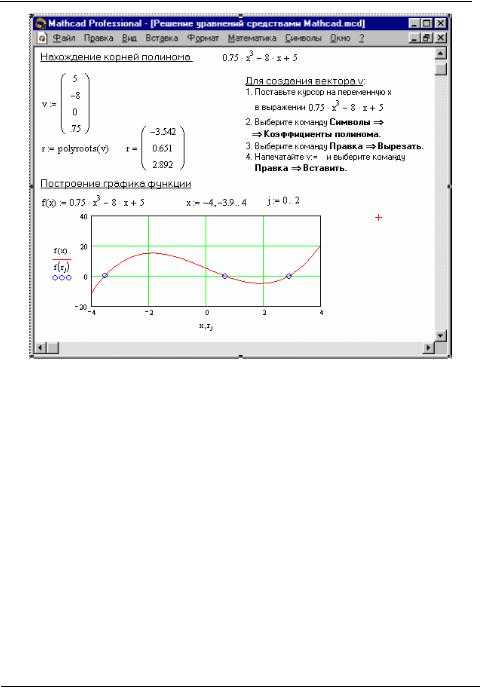
Для систем с параметрами рекомендуется варьировать значения параметров в небольшом диапазоне и наблюдать устойчивость решений. Если результат резко меняется, следует пересмотреть метод решения или уточнить модель.

Проверка решений также включает подстановку найденных значений обратно в исходные уравнения. Mathcad автоматически вычисляет значения выражений, что позволяет быстро выявить несоответствия или ошибки округления.

Обратите внимание на число значащих цифр в ответах – избыточное увеличение количества знаков после запятой часто не соответствует точности исходных данных и может вводить в заблуждение.

При численных методах решения (например, метод Ньютона или итерационные методы) важно контролировать критерии сходимости и количество итераций. При отсутствии сходимости или слишком большом числе шагов необходимо пересмотреть начальные приближения или изменить параметры метода.

Для комплексных систем рекомендуется построить графики переменных и функции невязки. Mathcad позволяет визуально оценить поведение решений и выявить возможные аномалии.

Если решение предполагает несколько корней, следует проверить все варианты, используя разные начальные условия, чтобы удостовериться в полноте найденных решений.

Решение систем с параметрами и переменными

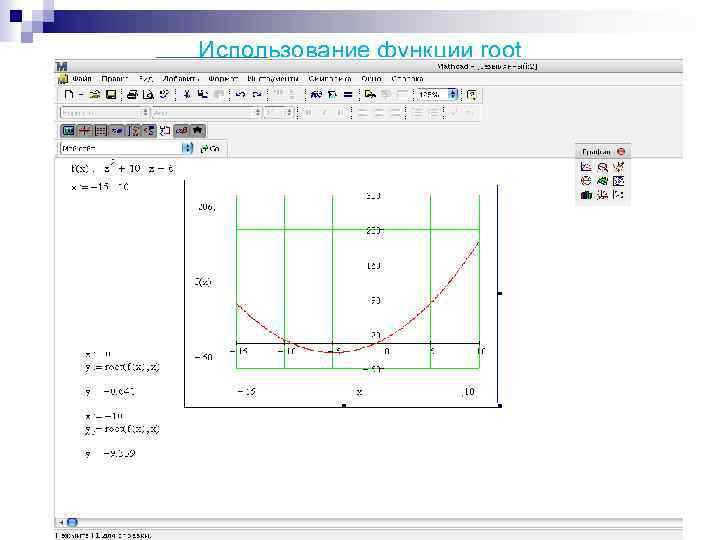
В Mathcad системы уравнений с параметрами решаются с помощью определения параметров как символических переменных. Для этого необходимо задать параметры через оператор «:=» до объявления системы, сохраняя их как свободные символы, а переменные – как неизвестные, подлежащие вычислению.

Функция Solve или SolveBlock применяется к системе, в которой уравнения записаны с использованием параметров. Mathcad возвращает решения в зависимости от заданных значений параметров, что позволяет проводить анализ чувствительности без повторного построения модели.

Для корректной работы важно явно указать, какие символы являются параметрами, а какие – переменными. Если параметр не определён, Mathcad трактует его как переменную, что может привести к ошибкам или неопределённым решениям.

В случае многообразия решений система должна быть преобразована с помощью дополнительных ограничений или условий на параметры. Например, можно задать ограничения через неравенства или определить диапазон допустимых значений параметров в виде условий.

Для автоматизации варьирования параметров удобно использовать циклы или встроенные таблицы значений, передавая параметры как входные данные в функцию решения. Это позволяет получить массив решений и построить графики зависимости переменных от параметров.

Если система включает нелинейные уравнения с параметрами, рекомендуется использовать численные методы решения с начальным приближением, учитывающим конкретные значения параметров. Это минимизирует вероятность сходимости к некорректным корням.

Подведение итогов: точное задание параметров, использование SolveBlock с условиями, контроль диапазонов параметров и применение численных методов с приближениями – ключевые моменты при работе с системами с параметрами в Mathcad.

Типовые ошибки при решении систем уравнений и их устранение

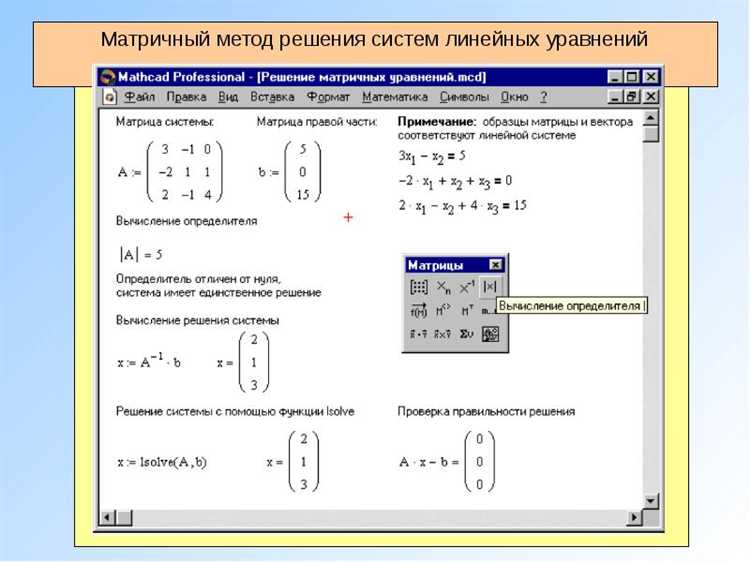
При решении систем уравнений в Mathcad часто встречаются ошибки, напрямую влияющие на корректность результата. Рассмотрим основные из них и способы их устранения.

• Неверное задание переменных и уравнений
  • Ошибка: переменные не объявлены или объявлены с ошибкой в именах.
  • Решение: использовать латинские буквы без пробелов и специальных символов. Проверять правильность написания переменных везде, где они используются.
• Отсутствие явного указания начальных приближений
  • Ошибка: Mathcad не находит решение из-за отсутствия начальных приближений для нелинейных систем.
  • Решение: задавать начальные приближения через аргумент начальных значений в функции решения (например, в функции find()).
• Использование операторов сравнения вместо присваивания
  • Ошибка: при формулировке системы вместо присваивания := используется знак равенства =.
  • Решение: в Mathcad для определения переменной использовать только оператор :=. Для уравнений применять оператор равенства = внутри функции решения.
• Неправильный ввод уравнений с отсутствием или избыточными скобками
  • Ошибка: неверное группирование выражений приводит к логическим ошибкам и неверным вычислениям.
  • Решение: внимательно проверять скобки, использовать автоматическую подсветку синтаксиса Mathcad для контроля корректности.
• Несоответствие размерности в векторных и матричных уравнениях
  • Ошибка: попытка решать систему с несовместимыми по размеру векторами или матрицами.
  • Решение: перед решением проверить размерности всех переменных, корректно задавать векторы и матрицы, использовать функции rows() и columns() для проверки.
• Игнорирование единиц измерения
  • Ошибка: переменные с разными единицами измерения смешиваются, что приводит к ошибочным результатам.
  • Решение: применять встроенную систему единиц Mathcad, согласовывать единицы до решения, отключать или приводить к общему виду.
• Отсутствие проверки решения
  • Ошибка: пользователь принимает численный ответ без подстановки обратно в уравнения для проверки.
  • Решение: всегда подставлять полученные значения в исходную систему для проверки точности решения.

Соблюдение этих рекомендаций значительно снижает количество ошибок и ускоряет получение корректных результатов при решении систем уравнений в Mathcad.

Вопрос-ответ:

Как в Mathcad задать систему уравнений для решения?

В Mathcad система уравнений задаётся с помощью оператора равенства, при этом каждое уравнение записывается отдельно, а затем все они объединяются в вектор или матрицу уравнений. Обычно используется оператор вектора, чтобы объединить уравнения в одну структуру, которая подаётся на вход функции решения. Например, если есть уравнения f1(x,y)=0 и f2(x,y)=0, то можно записать их в виде вектора: system := [f1(x,y), f2(x,y)].

Какие методы решения систем уравнений доступны в Mathcad?

Mathcad предоставляет несколько способов для решения систем уравнений. Наиболее часто применяются численные методы, такие как использование функции Find, которая работает по принципу поиска корня системы. Кроме того, можно применять аналитические методы, если уравнения простые и позволяют это. Для нелинейных систем обычно используют численное решение с начальным приближением, а для линейных систем — прямое решение через матрицы. Выбор метода зависит от вида уравнений и требуемой точности.

Как задать начальное приближение при решении нелинейной системы в Mathcad?

Для численного решения нелинейных систем в Mathcad важно указать начальное приближение — значения переменных, с которых начинается поиск решения. Обычно это делается через аргументы функции Find, где указываются переменные и их стартовые значения, например: Find(system, [x, y], [1, 1]). Начальное приближение влияет на сходимость и то, какое именно решение будет найдено, если у системы несколько корней.

Как проверить корректность решения системы уравнений в Mathcad?

После получения решения в Mathcad следует подставить найденные значения переменных обратно в исходные уравнения и проверить, насколько близки результаты к нулю или к правой части уравнений. Это можно сделать, вычислив значения уравнений с найденными корнями и посмотрев на погрешности. Если значения близки к нулю в пределах заданной точности, решение можно считать корректным.

Можно ли решать системы уравнений с большим количеством переменных в Mathcad и как это сделать?

Да, Mathcad позволяет решать системы с большим числом переменных, но при этом возрастает сложность и требования к вычислительным ресурсам. Чтобы решить такую систему, все уравнения и переменные нужно собрать в соответствующие векторы или матрицы и использовать функции решения с указанием начальных приближений для каждой переменной. Важно, чтобы размерность системы совпадала с количеством переменных. Для сложных систем рекомендуется разбивать задачу на части или использовать специализированные численные методы.

Как пошагово решить систему уравнений в Mathcad, если уравнения нелинейные?

Для решения нелинейной системы в Mathcad сначала нужно определить уравнения и переменные. Затем следует использовать встроенную функцию для численного решения, например, `root` или `find`. Шаги включают: 1) задайте начальные приближения для каждой переменной; 2) введите уравнения в виде выражений; 3) вызовите функцию решения, указав переменные и начальные приближения; 4) после выполнения проверьте, удовлетворяют ли найденные значения уравнениям. При необходимости корректируйте начальные значения, чтобы улучшить сходимость.