Как решать матрицы в mathcad prime

Mathcad Prime предлагает точные инструменты для работы с матрицами, включая их создание, преобразование и решение систем уравнений. Для начала необходимо задать матрицу с помощью встроенного редактора, используя оператор квадратных скобок и ввод числовых элементов через пробел или запятую.

Для решения системы линейных уравнений в виде матричного уравнения AX = B требуется определить матрицы A и B, затем использовать оператор обратной матрицы или функцию solve. В Mathcad Prime важно соблюдать корректный синтаксис для матричных операций, избегая ошибок несоответствия размерностей.

Практический совет – всегда проверяйте размерность и тип данных матриц перед вычислением. Если матрица A вырожденная, расчет обратной невозможен, и решение следует искать через методы псевдообратных или численного приближения. В Mathcad Prime предусмотрены функции для работы с такими случаями, что значительно расширяет возможности анализа.

Решение матриц в Mathcad Prime: пошаговая инструкция

Шаг 1. Создайте матрицу. Для этого введите выражение, например, A :=, затем выберите кнопку матрицы в панели инструментов и укажите размер, например, 3×3. Заполните элементы матрицы числами или переменными.

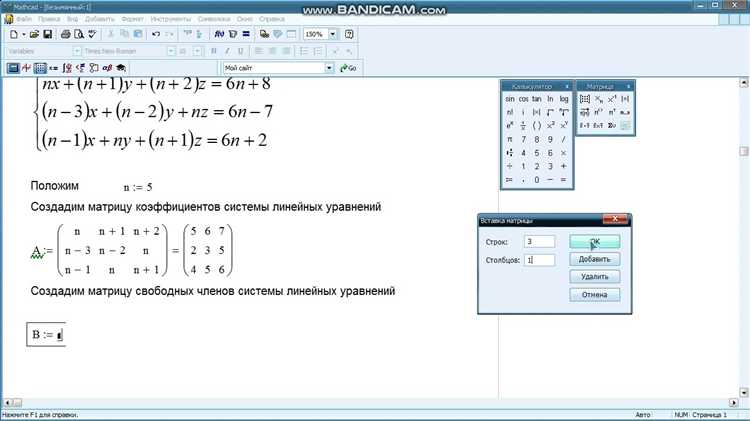
Шаг 2. Для решения системы уравнений с матрицей коэффициентов A и вектором свободных членов B введите B := и задайте вектор соответствующего размера.

Шаг 3. Используйте оператор обратной матрицы или встроенную функцию решения. Введите выражение X := A⁻¹ * B или воспользуйтесь функцией solve(A, B). Mathcad Prime автоматически вычислит результат.

Шаг 4. Проверьте размерность матриц, чтобы избежать ошибок: матрица A должна быть квадратной, а вектор B – столбцом с числом строк, равным размеру A.

Шаг 5. Для численного решения убедитесь, что все элементы матриц заданы как числовые значения. Если присутствуют переменные, определите их до вычислений.

Шаг 6. Чтобы получить детальный разбор решения, используйте функцию det(A) для вычисления определителя или rank(A) для проверки ранга матрицы.

Шаг 7. При необходимости визуализируйте результаты, вводите матрицы и векторы в области вычислений, а Mathcad отобразит их в привычном виде, позволяя проверять корректность ввода и решения.

Шаг 8. Для повторного использования решения сохраните рабочий лист, чтобы не вводить данные заново и быстро изменять параметры матриц и векторов.

Создание и ввод матрицы в Mathcad Prime

Для создания матрицы в Mathcad Prime выберите вкладку «Вставка» и нажмите «Матрица». В появившемся шаблоне укажите количество строк и столбцов. Размер матрицы можно изменить позднее через свойства объекта.

Ввод элементов происходит построчно. Активная ячейка выделяется синим контуром. Для перехода между элементами используйте клавиши Tab (вправо) и Shift+Tab (влево). Для перехода на следующую строку нажмите Enter.

Элементы матрицы допускают ввод чисел, выражений, переменных и встроенных функций. Для ввода дробей используйте клавишу «/», а для степеней – символ «^». После ввода формулы нажмите Enter, чтобы сохранить результат в ячейке.

Для быстрого создания диагональной матрицы заполните первую строку и столбец, а затем используйте встроенные функции, например, diag(), для автоматизации процесса. Аналогично, копирование и вставка элементов в матрицу работают через стандартные сочетания Ctrl+C и Ctrl+V.

Ошибки ввода отображаются красным цветом и сопровождаются подсказками. Исправляйте их непосредственно в ячейке. Для удаления матрицы выделите объект и нажмите Delete.

Определение размерности и типы матриц в Mathcad Prime

В Mathcad Prime размерность матрицы определяется количеством строк и столбцов, что задаётся сразу при её создании или изменении. Для инициализации матрицы используйте оператор двоеточия с указанием размеров, например, A:=2×3 создаст матрицу с 2 строками и 3 столбцами. Размерность можно получить с помощью функции rows(A) для строк и cols(A) для столбцов.

Mathcad Prime поддерживает матрицы числового, логического и текстового типов. В числовых матрицах хранятся вещественные или комплексные числа, логические содержат значения true или false, а текстовые состоят из строковых элементов. Тип матрицы определяется автоматически по содержимому, но можно явно задать тип с помощью функций преобразования.

Для работы с матрицами различной размерности рекомендуется использовать функции и операции, учитывающие их структуру. При вводе матриц обязательно соблюдать согласованность размеров: операции сложения и вычитания требуют одинаковых размеров, умножение – согласование столбцов первой и строк второй матриц.

Для изменения размерности матрицы применяют функцию resize(A, m, n), где m и n – новые размеры. При увеличении размера новые элементы инициализируются нулями, при уменьшении – происходит обрезка по заданным параметрам.

Важно помнить, что Mathcad Prime не поддерживает многомерные массивы выше двух измерений, поэтому все вычисления и операции ограничены двумерной матричной структурой.

Методы нахождения обратной матрицы в Mathcad Prime

В Mathcad Prime существует несколько эффективных способов вычисления обратной матрицы, каждый из которых подходит для разных задач и форматов исходных данных.

1. Использование встроенной функции inv()

   • Для квадратной матрицы A примените выражение inv(A).
   • Mathcad автоматически проверит размерность и выведет ошибку, если матрица вырождена.
   • Рекомендуется предварительно проверить определитель: det(A) ≠ 0.

2. Обратная матрица через оператор деления

   • Оператор обратного деления (A^-1 или A^(-1)) также позволяет найти обратную.
   • Данный способ полезен для быстрого вычисления в выражениях, не требующих отдельного сохранения результата.

3. Решение системы уравнений с единичной матрицей

   • Обратная матрица может быть найдена решением уравнения A * X = I, где I – единичная матрица того же размера.
   • В Mathcad задайте X := A^-1 или вычислите X := lsolve(A, I), если используется функция решения систем.
   • Метод полезен при необходимости одновременного решения системы и получения обратной.

4. Использование численных методов для больших матриц

   • Для больших или плохо обусловленных матриц рекомендуется использовать разложение LU или QR, доступное в расширенных библиотеках Mathcad.
   • Такой подход повышает точность и стабильность вычислений.
   • Пример: получить LU-разложение через lu(A), затем вычислить обратную, решая соответствующие системы.

Для корректного вычисления обратной матрицы в Mathcad Prime обязательно учитывать тип данных (вещественные или комплексные числа) и проверять условия существования обратной (например, через rank(A) и det(A)).

Вычисление определителя матрицы пошагово

В Mathcad Prime вычисление определителя матрицы реализуется через встроенную функцию det(). Для точного контроля процесса можно использовать разложение по минору или алгоритм Гаусса. Рассмотрим оба метода.

1. Создание матрицы

   Введите матрицу в Mathcad Prime с помощью оператора квадратных скобок и разделения элементов запятыми и точками с запятой. Например:

   A := [[1, 2, 3], [0, 4, 5], [1, 0, 6]]

2. Вычисление определителя встроенной функцией

   Введите:

   d := det(A)

   Mathcad вычислит определитель автоматически.

3. Разложение по минору (ручной подход)

   Для 3×3 матриц:

   • Выберите строку или столбец с максимальным количеством нулей для упрощения вычислений.
   • Вычислите алгебраические дополнения каждого элемента выбранной строки или столбца.
   • Определитель равен сумме произведений элементов на соответствующие алгебраические дополнения.

   В Mathcad это можно оформить так:

   minor := submatrix(A, i, j) – удаление i-й строки и j-го столбца.
   det(minor) – определитель полученной меньшей матрицы.

   Затем вычислить:

   det(A) = Σ (-1)^(i+j) * A[i,j] * det(minor)

4. Использование метода Гаусса для вычисления определителя
   • Преобразуйте матрицу A в верхнетреугольный вид с помощью элементарных операций над строками.
   • Записывайте количество перестановок строк (каждая перестановка меняет знак определителя).
   • Определитель равен произведению элементов главной диагонали умноженному на (-1) в степени числа перестановок.

   Mathcad позволяет реализовать это через пользовательские выражения, но проще использовать встроенную функцию для проверки.

Вычисление определителя в Mathcad Prime удобно комбинировать с разложением по минору для обучения и понимания процесса, а встроенная функция det() – для быстрой проверки результатов.

Решение систем линейных уравнений с помощью матриц в Mathcad Prime

В Mathcad Prime решение системы линейных уравнений удобно выполнять через матричные операции. Для системы вида Ax = b, где A – квадратная матрица коэффициентов, x – вектор неизвестных, b – вектор свободных членов, ключевой инструмент – оператор обратной матрицы или встроенная функция решения.

Первым шагом создайте матрицу A и вектор b в рабочих областях Mathcad, используя синтаксис прямоугольных скобок и точек с запятой для разделения строк. Например, A := [[1, 2], [3, 4]], b := [5, 6]. Следите, чтобы размерности совпадали: число строк A должно соответствовать размеру вектора b.

Для получения решения используйте оператор обратной матрицы A^-1 или функцию linalg::solve(A, b). Первый метод применим при невырожденной матрице A. Второй – более универсален и устойчив к численным ошибкам.

Например, выражение x := A^-1 * b даст вектор неизвестных x. Для систем с большой размерностью и возможной вырожденностью матрицы предпочтительнее использовать linalg::solve, вызывая его так: x := linalg::solve(A, b).

Mathcad Prime автоматически вычисляет обратную матрицу при использовании A^-1, но для повышения надежности рекомендуется проверять определитель det(A). Если det(A) ≈ 0, система либо вырождена, либо имеет бесконечное множество решений – в этом случае используйте псевдообратную матрицу или методы оптимизации.

Использование встроенных функций для умножения и транспонирования матриц

В Mathcad Prime операции с матрицами реализованы через специализированные функции, обеспечивающие точные и быстрые вычисления. Для умножения матриц применяется оператор умножения *, который автоматически проверяет совместимость размеров: число столбцов первой матрицы должно совпадать с числом строк второй. Например, если A – матрица размером 3×2, а B – 2×4, выражение A * B вернёт матрицу 3×4.

Транспонирование матриц в Mathcad Prime выполняется функцией transpose(). Она меняет местами строки и столбцы, что важно при корректировке размеров для операций умножения или при работе с симметричными матрицами. Вызов transpose(A) преобразует матрицу A размером m×n в матрицу размером n×m.

Для оптимизации вычислений рекомендуется использовать встроенные функции вместо ручного описания алгоритмов, что снижает риск ошибок и ускоряет обработку больших массивов данных. В случаях, когда необходимо умножить матрицу на вектор, Mathcad автоматически распознаёт вектор как частный случай матрицы и корректно выполнит умножение без дополнительного форматирования.

При работе с комплексными матрицами функция conj() позволяет получить сопряжённую матрицу, а в сочетании с transpose() – эрмитово сопряжённую, что важно для решений в инженерных и физических задачах. Например, выражение transpose(conj(A)) даёт эрмитово сопряжённую матрицу к A.

Mathcad Prime автоматически поддерживает матричные размеры, однако при использовании функций умножения и транспонирования важно следить за размерностью данных для предотвращения ошибок выполнения.

Обработка ошибок и проверка корректности вычислений с матрицами

Используйте встроенные функции Mathcad, такие как rows() и cols(), чтобы программно контролировать размерности перед вычислениями. Для проверки наличия нулевых строк или столбцов применяйте функцию any() к отдельным элементам.

Проверка корректности результата не ограничивается размерностью. При решении систем уравнений с матрицами следует дополнительно оценивать определитель (det) исходной матрицы. Значение det близкое к нулю сигнализирует о возможной вырожденности и нестабильности решения.

Для повышения точности проверяйте свойства итоговой матрицы: симметричность, положительную определённость или другие характерные признаки в зависимости от задачи. Mathcad Prime позволяет реализовать такие проверки с помощью простых логических выражений.

В случае сложных вычислений рекомендуется разбивать задачу на этапы с промежуточной проверкой результатов. Это поможет локализовать ошибки и понять источник некорректных значений.

Вопрос-ответ:

Как в Mathcad Prime задать матрицу для последующих вычислений?

В Mathcad Prime для создания матрицы достаточно ввести имя переменной, например A, затем ввести знак равно, после чего откроется поле для ввода элементов. Матрицу можно заполнять, вводя значения по строкам и столбцам, используя табуляцию или стрелки для перехода между ячейками. Размер матрицы можно изменять вручную, добавляя или удаляя строки и столбцы.

Какие операции с матрицами можно выполнить в Mathcad Prime и как их применять?

Mathcad Prime позволяет выполнять множество операций с матрицами: сложение, вычитание, умножение, транспонирование, обращение, вычисление определителя и другие. Чтобы сложить две матрицы, нужно использовать знак «+», умножение — знак «*». Для транспонирования применяется функция transpose(A), где A — имя матрицы. Для нахождения обратной матрицы используется inv(A). Важно, чтобы размеры матриц соответствовали требованиям операций — например, для умножения количество столбцов первой матрицы должно совпадать с количеством строк второй.

Как пошагово найти обратную матрицу в Mathcad Prime?

Для вычисления обратной матрицы в Mathcad Prime нужно: 1) Создать исходную матрицу A. 2) Ввести выражение inv(A), которое вызовет вычисление обратной матрицы, если она существует. 3) Если матрица необратима, программа выдаст ошибку или предупреждение. 4) Полученный результат можно сохранить в новую переменную для дальнейших вычислений. 5) Для проверки корректности можно умножить исходную матрицу на найденную обратную — результат должен быть единичной матрицей.

Как вычислить определитель матрицы в Mathcad Prime и для чего он нужен?

Определитель матрицы вычисляется с помощью функции det(A), где A — имя матрицы. Вводится выражение det(A), и Mathcad Prime рассчитывает значение определителя. Определитель помогает понять, является ли матрица обратимой — если он равен нулю, обратной матрицы не существует. Кроме того, определитель используется в различных математических задачах, таких как решение систем уравнений и анализ свойств матриц.

Можно ли решать системы линейных уравнений с помощью матриц в Mathcad Prime? Как это сделать?

Да, Mathcad Prime позволяет решать системы линейных уравнений, используя матрицы. Для этого составляется матрица коэффициентов A и вектор свободных членов B. Решение X находится как X = inv(A)*B, где inv(A) — обратная матрица. Вместо вычисления обратной матрицы можно воспользоваться встроенной функцией solve(A,B), которая автоматически определит решение системы. Такой подход удобен для быстрого получения результата и проверки решений.