Maple позволяет решать как линейные, так и нелинейные системы уравнений с точным контролем над каждым этапом. Прямая работа с командами solve, fsolve, LinearSolve и linalg делает возможным выбор между символьным и численным подходами. Это особенно удобно при анализе систем с параметрами или при необходимости отслеживания промежуточных результатов.
Для решения линейной системы символьно следует использовать solve({уравнения}, {переменные}). Например, система из двух уравнений x + y = 3, 2x — y = 0 записывается в Maple как: solve({x + y = 3, 2*x — y = 0}, {x, y}). Maple возвращает точный символьный результат без округлений, что особенно полезно при теоретических выкладках.
Если система содержит числовые коэффициенты с плавающей точкой или предполагается приближённое решение, применяется fsolve. Эта команда подходит для уравнений, не поддающихся символьному решению, например: fsolve({sin(x)+y=1, x^2+y^2=2}, {x, y}).
Для больших линейных систем предпочтительнее работать с матрицами. Команда LinearSolve решает уравнение A·X = B, где A – матрица коэффициентов, B – столбец правых частей. Создание матрицы производится с помощью Matrix(), а решение – LinearSolve(A, B). Это особенно полезно при решении задач с размерностью выше трёх переменных, где ручной ввод уравнений становится неэффективным.
При необходимости получить все промежуточные преобразования, следует активировать пошаговый режим через интерфейс Maple или использовать встроенную обучающую среду. Это позволяет анализировать каждый этап упрощения, подстановки и решения, а также отследить, где возникает возможная ошибка или неопределённость.
Как задать систему линейных уравнений в Maple
Для задания системы линейных уравнений в Maple необходимо использовать списки и встроенные функции. Пример: задать систему из двух уравнений с переменными x и y.
Ввод уравнений:
eq1 := 2*x + 3*y = 7: eq2 := -x + 4*y = 1:
Формирование системы уравнений:
sys := [eq1, eq2]:
Указание списка переменных:
vars := [x, y]:
Проверка корректности задания:
sys; vars;
Для решения используйте:
solve(sys, vars);
Если необходимо сохранить результат в переменную:
sol := solve(sys, vars);
Для получения численного приближенного решения примените:
fsolve(sys, vars);
При работе с системами большого размера используйте цикл или оператор seq для автоматической генерации уравнений, если структура повторяется.
Maple поддерживает задание коэффициентов с плавающей точкой, комплексных чисел и параметров. Убедитесь, что все переменные определены или остаются символическими.
Использование команды solve для нахождения общего решения

Команда solve в Maple применяется для аналитического решения систем уравнений. Для получения общего решения необходимо использовать список уравнений и список переменных, по которым ведётся решение.
- Запись уравнений в виде списка:
- Пример:
eqs := [x + y = 5, 2*x - y = 1];
- Пример:
- Указание переменных:
vars := [x, y];
- Вызов команды
solve:solve(eqs, vars);
Результатом будет общее решение в виде списка выражений. Если система несовместна, Maple вернёт пустой список. При недоопределённости система может содержать параметры (например, _t), обозначающие свободные переменные.
Для отображения решения в виде уравнений следует использовать опцию explicit=true:
solve(eqs, vars, explicit=true);Если система содержит параметры, решение может быть выражено через них. Для задания таких параметров можно воспользоваться опцией parametric:
solve(eqs, vars, parametric);Для систем с комплексными решениями можно указать домен:
solve(eqs, vars) assuming real;Команда solve работает с уравнениями любой сложности: линейными, нелинейными, с логарифмами, экспонентами и тригонометрией. Однако в случае громоздких систем целесообразно использовать solve совместно с simplify или expand для упрощения результатов.
Решение системы с параметрами и анализ зависимости от них
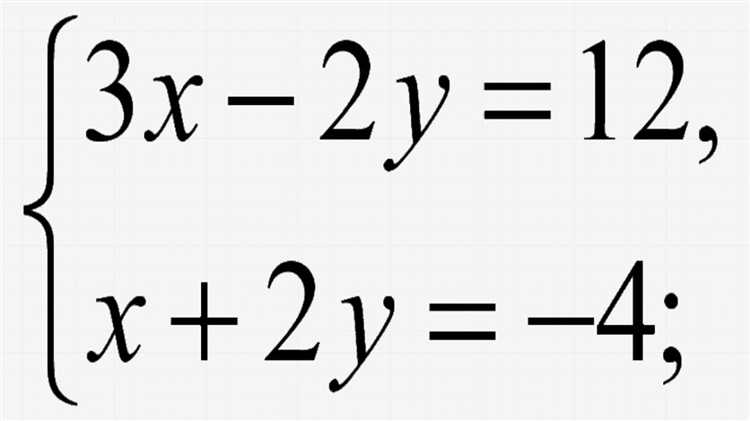
Для решения системы с параметрами в Maple удобно использовать функцию `solve` с указанием переменных и параметров. Пример системы:
eq1 := a*x + y = 1;
eq2 := x + b*y = 2;
Для решения относительно переменных x и y при параметрах a и b выполняется:
solve({eq1, eq2}, {x, y});
Если необходимо получить решение в виде функций от параметров, полезно использовать опцию parametric:
solve({eq1, eq2}, {x, y}, parametric);
Для анализа существования решений применяют определитель основной матрицы коэффициентов. В данном случае матрица:
A := Matrix([[a, 1], [1, b]]);
Determinant(A);
Если определитель равен нулю, система имеет либо бесконечно много решений, либо не имеет их вовсе. Значение определителя:
a*b - 1
Критическое значение: a*b = 1. Для анализа при этом значении подставляют в исходную систему и решают:
eq1 := a*x + y = 1;
eq2 := x + (1/a)*y = 2;
solve({eq1, eq2}, {x, y});
Если Maple возвращает пустое множество – решений нет. Если выражения содержат параметры – система совместна при определённых значениях параметров.
Для проверки всех случаев используют case analysis вручную или с помощью `solve` с условиями:
solve({eq1, eq2, a*b = 1}, {x, y});
Для построения графика зависимости переменных от параметра применяется `plot3d` или `implicitplot` (при численных значениях):
sol := solve({eq1, eq2}, {x, y});
plot3d(rhs(sol[x]), a = -5..5, b = -5..5);
При необходимости исключения переменной и получения уравнения зависимости параметров, используют `eliminate`:
eliminate({eq1, eq2}, x);
Этот метод позволяет определить область параметров, при которых система совместна. Для упрощения выражений используют `simplify`:
simplify(%);
Применение метода подстановки и исключения переменных
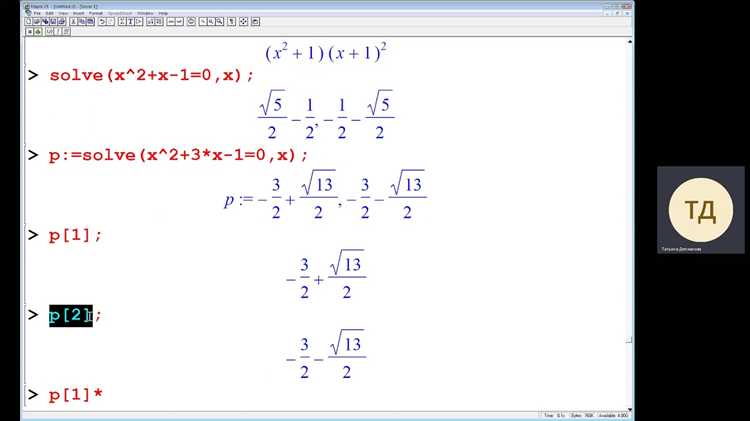
В Maple для решения систем линейных и нелинейных уравнений можно использовать методы подстановки и исключения переменных. Рассмотрим пошагово применение этих подходов на примерах.
Метод подстановки:
Рассмотрим систему:
x + y = 5 2x - y = 4
Шаг 1. Выразим одну переменную из первого уравнения:
solve(x + y = 5, y);
Результат:
y = 5 - x
Шаг 2. Подставим полученное выражение во второе уравнение:
subs(y = 5 - x, 2*x - y = 4);
Шаг 3. Решим полученное уравнение относительно x:
solve(2*x - (5 - x) = 4, x);
Результат:
x = 3
Шаг 4. Найдём y, подставив x = 3 в выражение y = 5 — x:
subs(x = 3, y = 5 - x);
Результат:
y = 2
Метод исключения:
Рассмотрим ту же систему:
x + y = 5 2x - y = 4
Шаг 1. Складываем уравнения, чтобы исключить y:
(x + y) + (2x - y) = 5 + 4;
Результат:
3x = 9 ⇒ x = 3
Шаг 2. Подставим x = 3 в любое из уравнений, например, в первое:
3 + y = 5 ⇒ y = 2
Автоматизация в Maple:
solve({x + y = 5, 2*x - y = 4}, {x, y});
Результат:
{x = 3, y = 2}
Оба метода можно комбинировать при решении более сложных систем. Для упрощения ручных вычислений рекомендуется пошагово использовать команды solve, subs и simplify в отдельных строках, отслеживая промежуточные выражения.
Решение системы нелинейных уравнений через fsolve

Для численного решения системы нелинейных уравнений в Maple используется функция fsolve. Она находит приближённое значение корней, основываясь на указанных начальных приближениях или интервалах.
Пример системы:
x^2 + y^2 = 4
exp(x) + y = 1
Ввод в Maple:
fsolve({x^2 + y^2 = 4, exp(x) + y = 1}, {x, y});
По умолчанию Maple ищет вещественные корни. Если система имеет несколько решений, результат зависит от выбранных начальных условий или интервалов.
Чтобы задать интервалы для переменных:
fsolve({x^2 + y^2 = 4, exp(x) + y = 1}, {x = -2..2, y = -3..3});
Если решение нужно только по одной переменной, остальные можно выразить заранее:
fsolve(x^2 + (1 — exp(x))^2 = 4, x = -2..2);
Для повышения надёжности стоит анализировать графики функций и задавать такие интервалы, в которых явно видна точка пересечения. Это снижает риск пропуска корней или получения некорректного результата.
При работе с несколькими переменными всегда задавайте диапазоны для всех переменных, иначе результат может быть неполным или отсутствовать.
Проверка решения с помощью подстановки и simplify
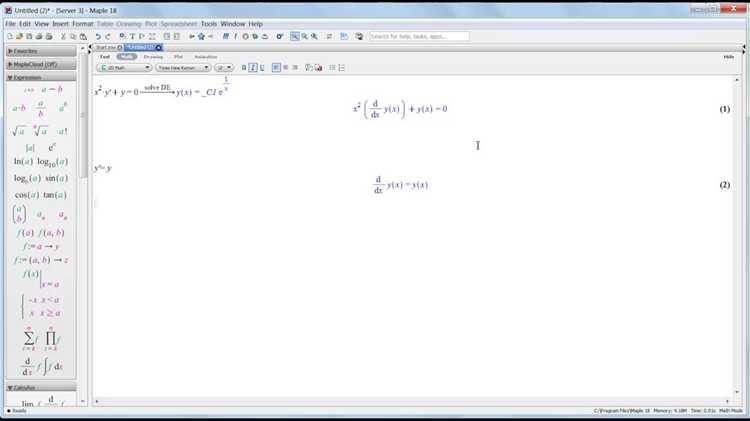
После нахождения решения системы уравнений в Maple важно убедиться в его корректности. Для этого подставьте найденные значения переменных обратно в исходные уравнения. В Maple это делается с помощью команды subs(), которая заменяет переменные на конкретные значения.
Например, если решение задано в виде списка sol := {x=1, y=2}, а система – уравнения eq1 и eq2, то проверка первого уравнения выглядит так: subs(sol, eq1). Аналогично для второго уравнения.
Для удобства оценки результата используют функцию simplify(), которая упрощает выражения и помогает выявить, равняется ли результат нулю или другому ожидаемому значению. Если после применения simplify(subs(sol, eq)) выражение превращается в 0, решение соответствует уравнению.
При системах с несколькими переменными процедуру повторяют для всех уравнений, чтобы проверить комплексность решения. Если хотя бы одно уравнение не сводится к тождеству, стоит пересмотреть процесс решения или проверить точность вычислений.
Использование simplify() помогает устранить мелкие арифметические погрешности, возникающие при численных вычислениях, и избежать ложного отрицательного результата при проверке решения.
Визуализация решений систем уравнений в Maple

Для построения графиков решений систем уравнений в Maple применяют функции plot и implicitplot из пакета plots. При работе с системами из двух переменных удобно использовать implicitplot для отображения каждого уравнения в одной системе координат.
Для запуска визуализации необходимо подключить пакет: with(plots):. Затем следует сформировать список уравнений и задать область построения графика, например, implicitplot([eq1, eq2], x = xmin..xmax, y = ymin..ymax, colors = [red, blue]);. Важно выбирать диапазоны координат, соответствующие ожидаемому месту расположения пересечений.
Для анализа множества решений полезно использовать параметр grid, регулирующий плотность сетки вычислений графика. Значение от 50 до 100 обеспечивает баланс между точностью и скоростью построения.
Для проверки пересечений графиков уравнений можно вывести на экран координаты точек пересечения с помощью команды solve с указанием переменных, после чего отметить эти точки на графике с помощью команды pointplot.
Использование цветовой дифференциации и легенд в графиках улучшает восприятие. Для добавления легенды используется опция legend = ["Уравнение 1", "Уравнение 2"]. Это особенно полезно при визуализации сложных систем с несколькими уравнениями.
Вопрос-ответ:
Как в Maple пошагово решить систему линейных уравнений?
Для решения системы линейных уравнений в Maple можно использовать команду `LinearSolve` или `solve`. Если хочется видеть этапы решения, стоит применять команду `Student[LinearAlgebra]:GaussElimination`, которая показывает поэтапное преобразование матрицы коэффициентов и векторов свободных членов. Для этого сначала задайте матрицу системы и вектор свободных членов, а затем вызовите метод Гаусса. Так можно отследить, как именно получаются решения.
Можно ли в Maple решить систему уравнений с параметрами и посмотреть ход вычислений?
Да, Maple позволяет работать с системами уравнений, где некоторые коэффициенты — параметры. Для этого вводят уравнения с параметрами, а затем используют команду `solve` с опцией `steps` или вызывают пакет `Student[Algebra]`, который показывает промежуточные этапы. В этом случае программа не просто выдает ответ, а демонстрирует, как меняются выражения в процессе, что помогает лучше понять влияние параметров на решение.
Как вывести пошаговое решение нелинейной системы в Maple?
Для нелинейных систем в Maple можно применить команду `solve` или `fsolve` для численного решения. Однако стандартных встроенных инструментов для детального пошагового разложения таких систем меньше. Можно вручную поэтапно решать уравнения, используя команды упрощения (`simplify`), подстановки и разложения, оформляя каждый шаг. Также доступны пакеты для алгебраических преобразований, которые помогают представить ход решения в понятном виде.
Какие команды в Maple помогают проверить правильность решения системы уравнений?
Для проверки решения системы достаточно подставить найденные значения переменных обратно в исходные уравнения. В Maple это можно сделать через команду `subs`, которая заменит переменные на найденные значения в уравнениях. Если после подстановки левая и правая части совпадают или разница равна нулю, решение верно. Также можно использовать команду `eval` для вычисления выражений с подставленными значениями.
Как в Maple задать и решить систему уравнений с большими размерами, чтобы видеть процесс?
Для систем с большим количеством уравнений и переменных лучше использовать матричный подход. В Maple задайте матрицу коэффициентов и вектор свободных членов. Затем применяйте методы из пакета `LinearAlgebra`, например, `GaussianElimination` с параметром, который показывает промежуточные шаги. Можно выводить результаты преобразований матриц на каждом этапе, что облегчает контроль и понимание процесса решения даже для крупных систем.
Как в Maple можно решить систему линейных уравнений и получить подробный разбор каждого шага?
Для решения системы линейных уравнений в Maple можно воспользоваться командой `LinearSolve` из пакета LinearAlgebra или встроенной функцией `solve`. Чтобы получить подробный разбор шагов, удобнее использовать пакет `Student[LinearAlgebra]`, который позволяет выводить промежуточные вычисления. Например, после загрузки пакета командой `with(Student[LinearAlgebra]):` можно применить функцию `LinearSystemStepByStep`, передав ей матрицу коэффициентов и столбец свободных членов. Maple покажет процесс приведения системы к ступенчатому виду, подстановки и нахождения решения, что помогает понять логику решения и проследить каждый этап.