Как решать уравнения в mathcad

Mathcad позволяет решать алгебраические, дифференциальные и трансцендентные уравнения с использованием как численных, так и символьных методов. Для начала достаточно определить переменные, задать исходное уравнение и использовать встроенные функции, такие как solve или оператор Given.

Решение начинается с ввода уравнения в явной или неявной форме. Например, для выражения x² + 3x − 4 = 0 используется символьная команда solve(x² + 3x − 4 = 0, x). Для численного метода – блок Given, где перечисляются условия, и применяется функция find(x). Mathcad автоматически различает типы уравнений и выбирает подходящий способ обработки.

Важно учитывать единицы измерения, так как Mathcad по умолчанию выполняет проверку размерностей. Несогласованные единицы вызывают ошибку. Если предполагается численное решение, все переменные должны иметь численные значения или быть выражены через заданные параметры.

Для систем уравнений создаётся блок Given с перечнем условий, после чего используется find(x, y, z) с указанием всех переменных. В случае символьного решения нескольких уравнений применяют solve({уравнение1, уравнение2}, {x, y}). Возможны также ограничения и параметры, задаваемые через неравенства в блоке условий.

Для повышения точности численных решений рекомендуется использовать команду assume с уточнением диапазона переменной. Это позволяет избежать ложных корней и ускоряет сходимость. Mathcad предоставляет средства визуализации графиков уравнений, что помогает оценить начальные приближения и поведение решений.

Как задать переменные и константы для уравнений

В Mathcad переменные и константы задаются непосредственно в рабочем листе с использованием оператора присваивания ← (знак двунаправленной стрелки). Для ввода этого символа нажмите клавишу : после имени переменной.

Для задания переменной введите её имя, затем нажмите :, после чего введите значение. Например:

x := 5

Эта запись создаёт переменную x со значением 5. Переменная становится доступной во всех выражениях, расположенных ниже по листу.

Константы задаются аналогично. Разницы в синтаксисе между переменной и константой нет. Константа – это переменная, значение которой не изменяется далее по ходу вычислений. Пример:

g := 9.81

Чтобы задать переменные-аргументы для уравнений, используйте символы, отличные от уже заданных. Например:

a := 3
b := 4
c := √(a² + b²)

Для многоразового использования рекомендуется использовать имена переменных без пробелов и специальных символов. Примеры корректных имён:

mass1
velocity
T_max

Если необходимо задать вектор или матрицу, используйте клавишу [. Например, для вектора:

v := [1 2 3]

Для определения диапазона переменных используйте оператор ... Например:

i := 0..10

Это создаёт переменную i, принимающую значения от 0 до 10 включительно. Диапазон можно использовать в циклах, графиках и индексировании.

Если необходимо ввести символическое выражение (например, x как переменную, а не как числовое значение), убедитесь, что значение не присвоено ранее. Для очистки используйте клавишу Del или команду очистки переменной через контекстное меню.

Ввод алгебраических уравнений в рабочее поле

Для ввода алгебраического уравнения в Mathcad, необходимо использовать математическое рабочее поле, активируемое щелчком левой кнопкой мыши в любой свободной области документа. После этого следуйте пошаговой инструкции:

Введите переменные и числовые коэффициенты, используя стандартную клавиатуру. Пример: x^2 + 3*x - 10.
Для ввода знака равенства, используйте клавишу = на клавиатуре. Это создаст оператор определения. Чтобы ввести уравнение, а не определение, нажмите Ctrl + = – появится знак равенства как логический оператор.
Если необходимо ввести выражение в виде функции, используйте круглые скобки. Пример: f(x) := x^2 - 4.
Для ввода систем уравнений размещайте каждое уравнение на новой строке. Чтобы задать систему, используйте операторы логического равенства и объединяйте уравнения с помощью оператора and.
Корректная расстановка скобок обязательна – Mathcad строго следует правилам математического приоритета операций. Используйте ( ) даже при простой вложенности.
Для обращения к символическим операциям используйте комбинацию Ctrl + . после ввода уравнения. Mathcad отобразит меню символических команд, таких как solve или simplify.

Все выражения интерпретируются в соответствии с текущими единицами измерения, если они заданы, поэтому при работе с безразмерными уравнениями отключайте проверку единиц в свойствах документа.

Использование функции solve для поиска неизвестных

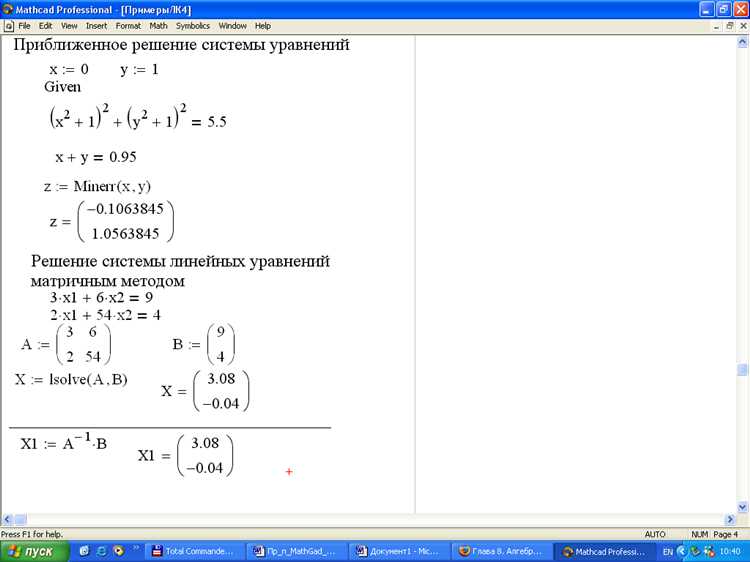
Функция solve в Mathcad применяется для нахождения значений переменных, удовлетворяющих заданной системе уравнений. Она используется только внутри блока Given-Find, что требует соблюдения определённой структуры записи.

Создайте блок уравнений. Начните с ключевого слова Given, которое указывает Mathcad на начало системы уравнений.
Запишите уравнения в виде выражение = выражение, избегая оператора :=, который обозначает присваивание.
После уравнений используйте оператор Find(переменная) или Find(переменная1, переменная2, ...) для поиска одной или нескольких неизвестных.

Пример:

Given
x + y = 10
x - y = 2
Find(x, y)

Результатом выполнения блока станет численное решение системы: значения x и y, удовлетворяющие обоим уравнениям.

Убедитесь, что количество уравнений не меньше количества неизвестных.
Все переменные должны быть объявлены ранее или быть единственными неизвестными в уравнении.
Для работы с неявными функциями используйте root или minerr, а не solve.
Функция solve не предназначена для символьного решения. Используйте её только для численного поиска значений.

Mathcad автоматически выбирает численные методы решения. Уточнение начальных условий или ограничений возможно через присвоение значений переменным до блока Given.

Настройка системы уравнений и множественных переменных

Для ввода системы уравнений в Mathcad используйте блок уравнений (блок решателя). Он создаётся через вкладку «Math» → «Solve Block» или с помощью вставки ключевых слов «Given», «Find» или «Solve». Все переменные и уравнения, включённые в блок, должны быть расположены между начальной меткой «Given» и функцией поиска решения.

Каждое уравнение вводится на новой строке. Используйте знак равенства = для задания математического равенства, а не символ присваивания :=. Все переменные в системе должны быть объявлены либо явно в предыдущих выражениях, либо использованы напрямую в уравнениях внутри блока.

Имена переменных не могут совпадать с зарезервированными функциями. Например, избегайте использования имён x и y, если они уже определены в другом месте рабочего листа.

Для решения системы уравнений используйте функцию Find(var1, var2, ...), где перечислены все переменные, подлежащие вычислению. Убедитесь, что количество уравнений соответствует количеству неизвестных. В противном случае Mathcad выдаст сообщение об ошибке несбалансированной системы.

При работе с нелинейными системами рекомендуется задать начальные приближения с помощью выражений var := value до начала блока «Given». Это повышает шанс успешной сходимости решателя.

Для контроля результатов используйте выражения var = после функции Find(), чтобы вывести численные значения найденных переменных на рабочем листе.

Применение блока solve для численного решения

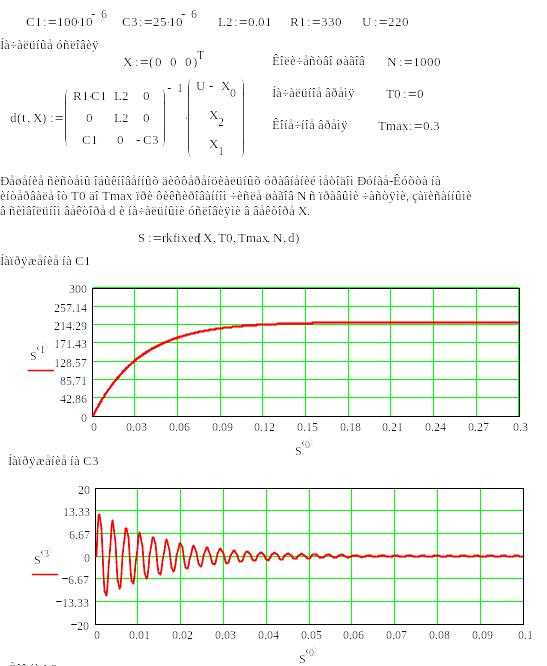
Блок solve используется в Mathcad для численного решения систем нелинейных уравнений. Для его создания выберите Insert → Solve Block или используйте комбинацию клавиш Ctrl+Shift+B. Блок начинается оператором Given и завершается функцией, например, root или minerr.

После оператора Given вводятся уравнения или неравенства. Каждый элемент системы записывается в отдельной строке. Для задания переменных используются обычные математические обозначения, а не символические операторы. Все параметры должны быть определены до блока или в нем самом.

В качестве метода решения чаще всего используется функция find(имя_переменной), которая возвращает численное значение переменной, удовлетворяющее системе. Перед использованием find необходимо задать начальное приближение для каждой переменной. Это делается вне блока или внутри него, например: x := 1. Начальные приближения сильно влияют на результат, особенно при наличии нескольких корней.

Функция minerr используется, если система несовместна – она минимизирует сумму квадратов невязок. В отличие от find, она не требует точного равенства уравнений, что полезно для работы с экспериментальными данными.

При решении многомерных систем рекомендуется явно указывать все уравнения, избегая встроенных выражений с неопределенным числом операций. Это повышает устойчивость решения и снижает вероятность ошибок.

Решение уравнений с параметрами и условиями

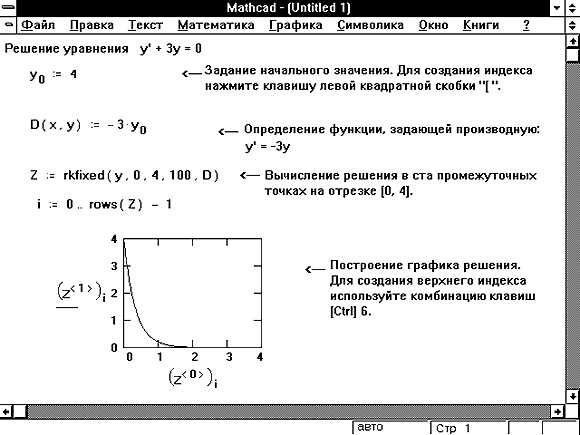
Для решения уравнений с параметрами в Mathcad необходимо использовать переменные, которым присваиваются значения до или после вычисления основного выражения. Объявление параметров осуществляется с помощью оператора присваивания (:=). Например:

a := 3 x := 5 eq := a·x + 2 = 17

Для поиска неизвестного при заданном параметре используется функция solve или символическое решение через solve, x после нажатия клавиши [Ctrl] + [. (ввод символического оператора).

Если параметр должен варьироваться в пределах определённых значений, используется диапазонная переменная. Например:

a := 1, 2..5

При этом решение оформляется как вектор. Чтобы получить набор решений, необходимо задать выражение в виде функции, зависящей от параметра, и использовать цикл через функцию for или встроенную возможность векторизации (горизонтальная стрелка).

Для включения условий применяется логическая функция if. Например:

if a ≠ 0 then solve(a·x + 2 = 10, x)

При множественных условиях рекомендуется использовать вложенные if или оператор piecewise для разветвлённой логики. Также полезна функция root для численного решения с указанием начального приближения:

root(a·x² + b·x + c, x, x₀)

Где x₀ – начальное значение, близкое к ожидаемому корню. Это особенно важно при зависимости коэффициентов от параметров.

Для автоматического подбора параметров при заданных условиях применяется функция minerr, минимизирующая остаток уравнения. Например:

minerr(x) := |a·x + 2 - 10|

После чего используется встроенный численный оптимизатор minimize:

minimize(minerr, x)

Все параметры и переменные должны быть заданы до момента вызова функции решения. Следите за единицами измерения, Mathcad учитывает их автоматически, и несоответствие может привести к ошибке.

Типичные ошибки при решении уравнений и способы их устранения

В Mathcad часто встречаются ошибки, связанные с неправильным вводом уравнений. К примеру, пропуск знака равенства или использование знака присваивания «:=» вместо «=» приводит к тому, что Mathcad воспринимает выражение как определение, а не уравнение. Для решения следует обязательно использовать «=» и проверить, что уравнение содержит именно этот знак.

Ошибка в обозначениях переменных: если переменная не определена или её имя совпадает с функцией Mathcad, решение не будет найдено. Для проверки стоит выделить все переменные и убедиться, что они не конфликтуют с системными функциями.

Некорректный синтаксис функций – частая причина сбоев. Например, забытые скобки в тригонометрических функциях (sin x вместо sin(x)) приводят к ошибке вычисления. Решение – использовать скобки всегда, даже для одиночного аргумента.

Уравнения с несколькими решениями требуют задания области поиска корня. Без указания начального приближения или диапазона Mathcad может не найти решение или вернуть только одно из них. Рекомендуется использовать функцию root с параметрами, задающими начальное приближение.

При решении дифференциальных уравнений часто забывают задать начальные условия, что делает уравнение неопределённым. В Mathcad начальные условия задаются через точечные значения функции в конкретных точках, их отсутствие приводит к ошибке. Необходимо четко указывать условия до начала решения.

Если уравнение содержит параметры, которые не определены численно, Mathcad не сможет найти корень. Все параметры должны иметь числовые значения до запуска решения.

Ошибки округления или слишком грубое начальное приближение приводят к медленной сходимости или отсутствию решения. Рекомендуется использовать точные числовые значения для начального приближения и проверять результат на нескольких шагах.

Сохранение и документирование решения в Mathcad

Для сохранения решения в Mathcad используйте функцию «Сохранить» (Ctrl+S) или «Сохранить как» для создания отдельной копии файла с расширением .xmcd. Рекомендуется называть файлы с указанием темы задачи и даты для удобного поиска, например, «Уравнение_2025_05_18.xmcd».

Документирование решения начинается с добавления текстовых блоков, где кратко фиксируются исходные данные, выбранный метод и ключевые шаги. Используйте встроенные текстовые области Mathcad, чтобы выделить пояснения прямо в рабочем листе рядом с расчетами.

Для улучшения читабельности структурируйте лист: применяйте заголовки и подзаголовки, используйте маркеры и нумерацию. Вставляйте комментарии к важным формулам, объясняя их назначение и логику. Это облегчает проверку и повторное использование.

Экспорт готового решения доступен в формат PDF через меню «Файл» → «Экспорт» → «PDF». Перед экспортом проверьте корректность отображения всех блоков и формул. В PDF сохраняются интерактивные элементы, что удобно для презентаций и отправки коллегам.

Для архивирования проектов можно создавать резервные копии в облачных хранилищах или на внешних носителях. При этом рекомендуется сохранять не только итоговый файл, но и промежуточные версии, фиксируя изменения на каждом этапе.

Вопрос-ответ:

Как задать уравнение в Mathcad для последующего решения?

Для начала нужно ввести уравнение с использованием знака равенства. При этом переменные указываются без пробелов, а само уравнение должно быть корректным с точки зрения синтаксиса Mathcad. Затем стоит определить, какие переменные будут искомыми, и использовать специальные функции решения, например, root или solve, чтобы получить ответ.

Какие способы решения нелинейных уравнений доступны в Mathcad?

Mathcad предоставляет несколько методов для решения нелинейных уравнений. Один из самых распространённых – численный поиск корня с помощью функции root, где задаётся уравнение и начальное приближение. Также можно применять встроенный блок решения систем уравнений, если требуется работать с несколькими уравнениями одновременно. Важно корректно выбрать начальные параметры, чтобы найти правильный корень.

Как вывести в Mathcad пошаговое решение уравнения?

Хотя Mathcad не показывает автоматические шаги решения, можно вручную оформить процесс: последовательно записать преобразования уравнения в текстовых полях, а рядом – вычислить значения на каждом этапе с помощью формул. Такой подход помогает лучше понять логику и наглядно отследить ход решения, что удобно для учебных целей.

Можно ли решать системы уравнений в Mathcad, и как это сделать?

Да, в Mathcad возможно решать системы уравнений. Для этого уравнения записываются в виде массива или отдельных выражений, а затем применяется функция solve или root с вектором переменных. Важно задать начальные значения для каждой переменной, чтобы программа смогла найти решение. Полученный результат отображается в виде набора значений для каждой переменной системы.

Как настроить Mathcad для решения уравнений с параметрами?

Если уравнение содержит параметры, их можно определить как отдельные переменные в начале документа. При решении уравнения следует указывать эти параметры как фиксированные значения. Это позволяет легко менять параметры и наблюдать, как меняется результат решения. Такой способ помогает анализировать зависимость корней уравнения от разных факторов.

Как в Mathcad задать уравнение для решения и какие есть способы его ввода?

В Mathcad уравнение для решения можно ввести напрямую в виде выражения с переменной, например, y = x^2 — 4. Для численного решения используют встроенные функции, такие как root или find, где нужно указать уравнение и начальное приближение. Можно также задавать системы уравнений, выписав каждое уравнение в отдельной строке и объединив их в вектор. Важно правильно оформить уравнение, чтобы Mathcad понял, что его нужно решать, а не просто вычислять.