Как решать в mathcad

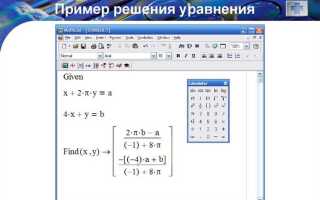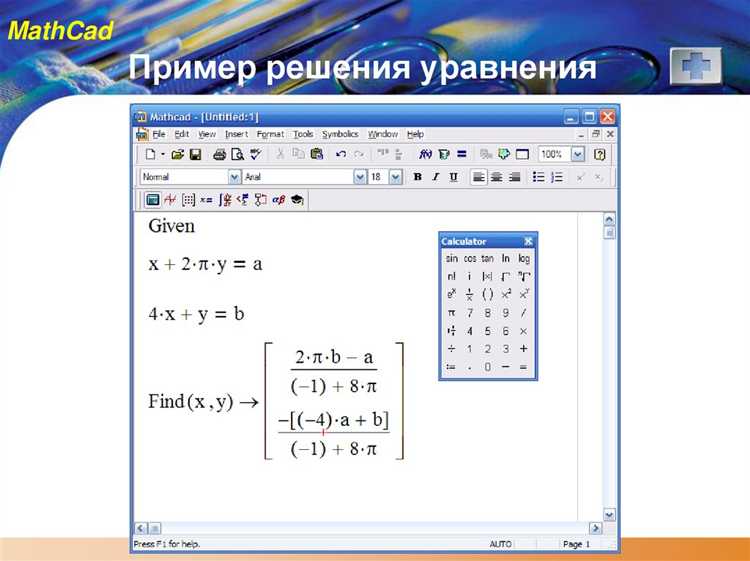
Mathcad предоставляет мощные инструменты для аналитического и численного решения уравнений любой сложности. Основой работы является ввод уравнения в стандартной математической нотации, что значительно упрощает восприятие и позволяет быстро выявить ошибки. Для начала необходимо определить переменные и задать уравнения в виде выражений с использованием оператора равенства (=), а не знака присваивания.

Решение систем уравнений выполняется через функцию solve, которая принимает набор уравнений и переменные для поиска. Важно задать начальные приближения, особенно для нелинейных задач – это повышает точность и стабильность результата. Mathcad поддерживает как символьное, так и численное решение, что позволяет оптимально выбрать метод в зависимости от задачи.

Для оптимизации вычислений рекомендуется использовать встроенные функции и избегать избыточных вычислительных выражений. Важно внимательно следить за размерностью единиц измерения, поскольку Mathcad автоматически учитывает их при расчетах, что снижает риск ошибок при конвертации. Правильное структурирование задачи и последовательный подход к вводу уравнений обеспечивают надежные и воспроизводимые результаты.

Настройка рабочей области для решения уравнений

Перед началом работы в Mathcad важно оптимизировать рабочую область для удобного и эффективного ввода уравнений. Рекомендуется создать отдельный лист или секцию, где будут сосредоточены все переменные и уравнения, что упростит навигацию и редактирование.

Для удобства ввода уравнений включите панель математических символов через меню «Вид» → «Панель инструментов». Это ускорит ввод сложных выражений и исключит ошибки синтаксиса. Включите режим автоматической подстановки операторов и функций, чтобы Mathcad распознавал введённые команды и корректно их форматировал.

Установите единицы измерения через панель «Units» для всех физических величин до ввода уравнений. Это предотвратит ошибки при вычислениях и обеспечит корректное согласование размерностей.

Используйте группы и заголовки для логического структурирования блока уравнений. Это позволит быстро переходить к нужным элементам и упорядочить рабочую область.

Настройте масштаб листа и размер шрифта так, чтобы уравнения были чётко видны и занимали оптимальное пространство. Для этого используйте вкладку «Вид» → «Масштаб».

Рекомендуется сохранять шаблоны с типовой настройкой и стандартными уравнениями, чтобы сократить время подготовки новой задачи. Для повторного использования используйте функцию «Сохранить как шаблон».

Ввод и редактирование математических выражений

В Mathcad ввод выражений происходит непосредственно в рабочей области документа. Для создания нового выражения нажмите клавишу «=» – курсор автоматически перейдет в режим ввода формулы. Для написания степеней используйте сочетание клавиш «^», дроби вводятся через «/», а скобки добавляются автоматически для сохранения порядка операций.

Редактирование формул происходит в месте их расположения: двойной клик по выражению переводит его в режим редактирования. Для быстрого изменения степени, индексов или функций можно использовать контекстное меню, доступное по правому клику, где есть стандартные математические операторы и функции.

При вводе сложных выражений используйте панели инструментов с математическими символами и шаблонами, например, для интегралов, производных или суммирования. Mathcad автоматически форматирует выражение, сохраняя визуальную читаемость и математическую точность.

Для корректного вычисления выражений следите за правильным использованием переменных и скобок. При необходимости добавляйте комментарии к выражениям с помощью текстовых блоков рядом с формулами, чтобы обеспечить понятность модели.

Используйте клавиши стрелок для перемещения внутри формулы без выхода из режима редактирования. Для удаления символов применяйте Backspace или Delete. Если требуется заменить часть выражения, выделите её и введите новую формулу, она заменит выделенное содержимое.

Решение алгебраических уравнений с помощью встроенных функций

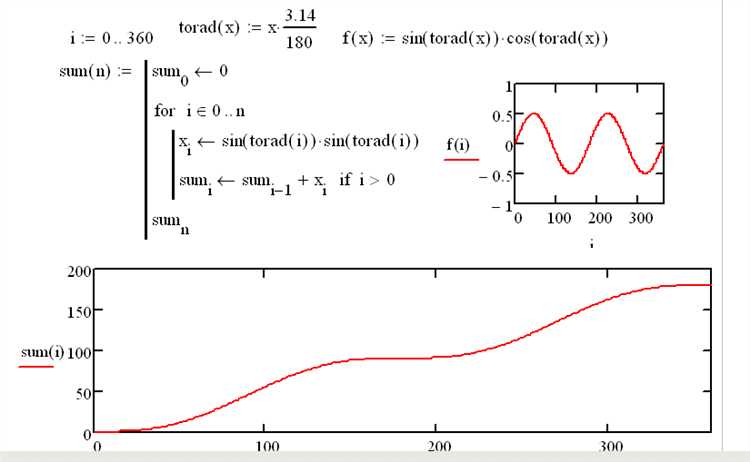
В Mathcad для решения алгебраических уравнений применяются функции solve и root, каждая из которых предназначена для разных задач. solve подходит для систем уравнений и позволяет получать точные аналитические решения при наличии таковых, в то время как root ориентирована на численный поиск корней.

Для уравнений вида f(x) = 0, где f – выражение от одной переменной, достаточно вызвать root с указанием начального приближения:
x0 := root(f(x), x, x_start). Выбор начального приближения x_start критичен для сходимости метода и получения нужного корня.

Если уравнение сложнее или включает несколько переменных, применяется solve:
solve({уравнение}, {переменная}). Mathcad автоматически анализирует выражение и возвращает решение в аналитическом виде, если это возможно. В противном случае – сообщает о невозможности решения.

Для систем из нескольких уравнений нужно передать все уравнения и переменные в виде множества:
solve({f1=0, f2=0, ...}, {x, y, ...}). Mathcad возвращает структуру с решениями по каждой переменной. В случае неоднозначности решений рекомендуется задавать дополнительные условия или ограничивать область поиска.

Практический совет: перед решением следует упростить уравнение с помощью встроенных функций simplify или expand для минимизации ошибок и ускорения вычислений. При численном решении проверяйте значения функции в окрестности найденного корня, чтобы удостовериться в правильности результата.

Использование численных методов для сложных задач

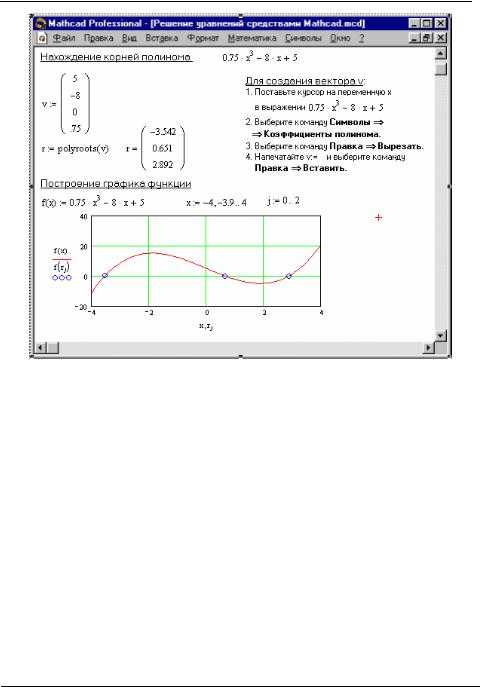
Mathcad предоставляет встроенные инструменты для численного решения уравнений и систем, когда аналитический подход невозможен или слишком трудоёмок. Для таких задач наиболее эффективны методы Ньютона, секущих и метод простых итераций, реализуемые через функции root, FindRoot и SolveBlock.

При работе с nonlinear уравнениями рекомендуется задавать начальное приближение максимально близко к ожидаемому корню, чтобы избежать сходимости к ложным решениям. В Mathcad можно использовать параметр initial_guess в функциях решения, что значительно повышает точность и скорость вычислений.

Для систем уравнений оптимальным считается применение метода Ньютона с аналитическим вычислением якобиана, который Mathcad позволяет автоматизировать через оператор jacobian(). Такой подход сокращает количество итераций и минимизирует ошибки округления.

В случае жёстких задач, где функции имеют резкие перепады или несколько корней, полезно использовать сеточный поиск с последующим уточнением найденных приближений численными методами. Mathcad поддерживает циклы и условные конструкции, что позволяет автоматизировать этот процесс.

Необходимость контроля сходимости решается путем анализа изменения значений переменных между итерациями. В Mathcad удобно реализовать условие выхода из цикла по достижении заданной точности, используя встроенные логические операторы.

Для задач оптимизации, связанных с уравнениями, Mathcad предлагает функции minimize и maximize, которые используют численные методы градиентного спуска и сопряжённых градиентов. Эти методы подходят для поиска экстремумов в ограниченных областях переменных.

Важной рекомендацией является аккуратная проверка граничных условий и ограничений, задаваемых в Mathcad через условные операторы, так как их нарушение может привести к некорректным решениям или отсутствию сходимости.

Использование численных методов в Mathcad требует грамотного выбора метода, настройки параметров и проверки результатов. Это гарантирует точность и стабильность вычислений при решении сложных задач, которые невозможно решить классическими аналитическими способами.

Построение графиков для проверки решений

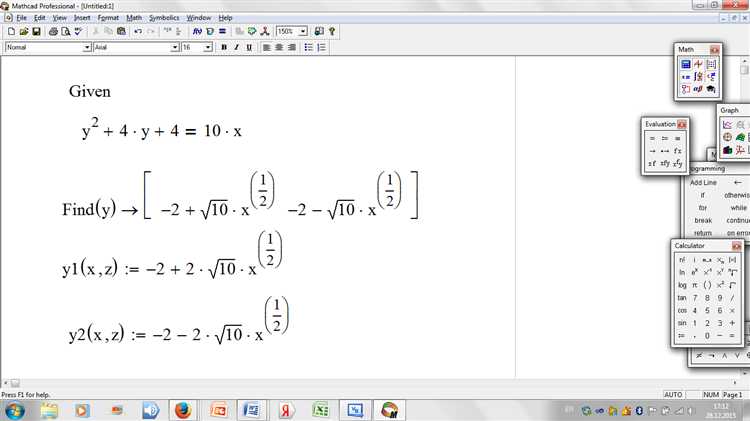
Графический анализ в Mathcad помогает быстро визуализировать поведение функции или уравнения и удостовериться в корректности найденного решения. Для проверки решений важно использовать точные параметры построения и правильный выбор типов графиков.

1. Выбор переменных и диапазона:
   • Определите независимую переменную, по которой строится график.
   • Укажите конкретный диапазон значений переменной, отражающий интересующий интервал (например, от -10 до 10 с шагом 0.1).
   • Используйте параметры функции Range для создания массива точек: x := -10, -9.9 … 10.
2. Построение графика функции или уравнения:
   • Введите выражение для функции, полученной в результате решения, или подставьте найденное значение.
   • В Mathcad используйте компонент графика (например, XY Plot) и задайте оси X и Y с соответствующими переменными.
   • При необходимости добавьте несколько функций для сравнения (например, исходное уравнение и найденное решение).
3. Анализ графика для проверки:
   • Проверьте точки пересечения с осью X – корни уравнения должны совпадать с решениями.
   • Обратите внимание на непрерывность и характер поведения графика в критических точках.
   • Если решение предполагает несколько корней, убедитесь, что график отражает все соответствующие пересечения.
4. Использование дополнительных функций Mathcad:
   • Воспользуйтесь инструментами масштабирования для точного изучения отдельных участков графика.
   • Добавляйте сетку и подписи осей для улучшения восприятия данных.
   • Используйте возможность наложения графиков, чтобы сравнить разные методы решения или различные варианты параметров.
5. Типичные ошибки при построении графиков:
   • Недостаточно мелкий шаг по переменной – приводит к искажению формы графика.
   • Слишком узкий диапазон – не позволяет увидеть всю картину решения.
   • Отсутствие проверок на области определения функции – возможны «пробелы» или ложные значения.

Работа с системами уравнений в Mathcad

Mathcad позволяет эффективно решать системы уравнений как линейного, так и нелинейного типа, используя встроенные функции и удобный интерфейс.

Основные этапы работы с системами уравнений в Mathcad:

1. Определение переменных: Переменные в системе задаются через знак равенства, например, x:=, y:=.
2. Запись уравнений: Уравнения вводятся в форме выражений с равенствами, например, eq1:= 2*x + 3*y = 7.
3. Создание вектора уравнений: Для решения системы необходимо объединить все уравнения в вектор, например, eqs := [eq1, eq2].
4. Вызов функции решения: Для поиска корней используется функция solve() или root() в зависимости от версии Mathcad. Например, roots := solve(eqs, [x, y]).
5. Задание начальных приближений: При решении нелинейных систем важны стартовые значения, задаваемые непосредственно перед вызовом функции решения.

Особенности работы с нелинейными системами:

• Используйте root() для поиска решений с указанием начального приближения: root(eqs, [x, y], [x0, y0]).
• Для ускорения сходимости укажите корректные начальные приближения, исходя из анализа графиков или физического смысла задачи.
• Обратите внимание на единицы измерений – Mathcad учитывает их при вычислениях, что помогает избежать ошибок.

Линейные системы удобно решать с помощью встроенных операторов матриц:

• Запишите систему в виде матричного уравнения A·X = B, где A – матрица коэффициентов, X – вектор переменных, B – вектор свободных членов.
• Используйте оператор обратной матрицы: X := A^(-1) · B.
• В Mathcad доступна функция lsolve(A, B) для более стабильного и быстрого решения.

Советы для точного решения:

• Проверяйте размерность векторов и матриц перед решением.
• Избегайте использования одинаковых имен переменных в разных частях документа.
• При сложных системах разбивайте их на подзадачи и проверяйте промежуточные результаты.

Обработка ошибок и диагностика расчетов

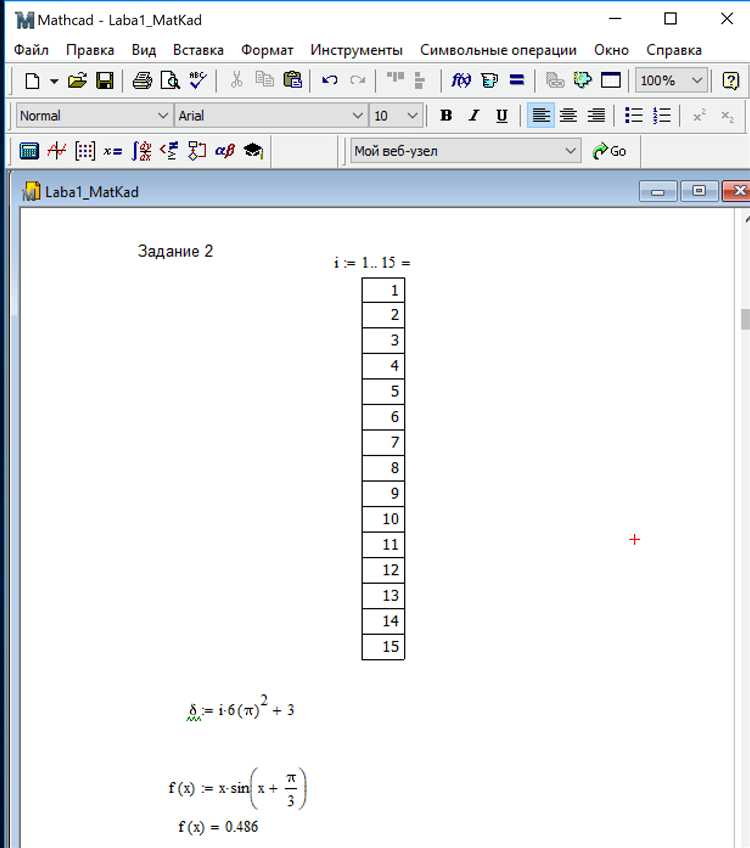
Mathcad автоматически проверяет синтаксис и логическую корректность выражений. Ошибки отображаются в виде красных меток или сообщений об ошибках при наведении курсора. Для локализации проблемы необходимо сначала проверить правильность определения всех переменных и единиц измерения. Mathcad чувствителен к несовпадению размерностей, даже если численные значения корректны.

Если выражение не вычисляется, проверьте последовательность определения переменных. Mathcad обрабатывает выражения сверху вниз и слева направо. Попытка использовать переменную до её определения вызывает ошибку «This variable is undefined».

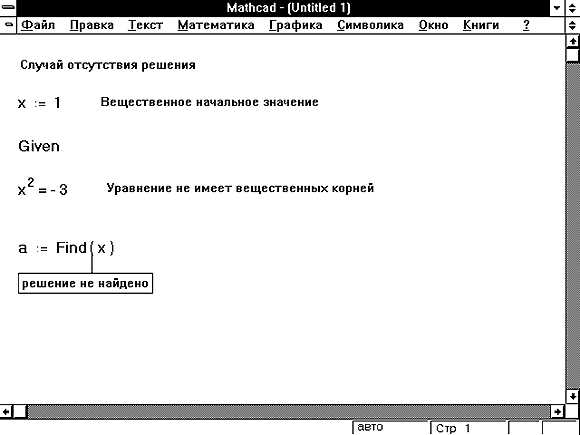
При решении уравнений с помощью функции solve или блока Given–Find убедитесь, что заданы все уравнения и начальные приближения. Ошибка «No solution found» часто указывает на отсутствие начальных условий или их неподходящие значения. Изменение начальных приближений может помочь найти решение в другой области.

Для систем с несколькими уравнениями используйте оператор stacked equations, избегая неопределённости переменных. Диагностируйте решение по поведению графиков – например, резкие скачки могут свидетельствовать о разрывах или делении на ноль.

Используйте встроенные функции trace и debug в скриптах на встроенном языке для отслеживания значений на каждом шаге. Это особенно полезно при программировании пользовательских функций, где стандартные средства диагностики не отображают внутренних ошибок.

Для устранения проблем с единицами временно отключите контроль размерностей с помощью команды Unit System → None, чтобы убедиться в правильности численной части выражений. После отладки обязательно верните контроль единиц.

Изучайте тип ошибки, отображаемой в окне сообщений: Mathcad классифицирует их по категориям (синтаксические, логические, вычислительные). Это позволяет сразу определить тип нарушений и не тратить время на перебор всех возможных причин.

Экспорт и сохранение результатов решения задач

Для сохранения вычислений в Mathcad используйте встроенные механизмы экспорта. Чтобы сохранить документ в формате PDF, выберите пункт меню «Файл» → «Экспорт» → «PDF». Этот формат сохраняет точное визуальное представление расчетов и графиков, включая все аннотации и единицы измерения.

Если необходимо перенести численные результаты в сторонние приложения, воспользуйтесь экспортом в Excel. Для этого выделите область с результатами, нажмите правой кнопкой мыши и выберите «Скопировать как таблицу». Далее вставьте содержимое в Excel, где данные сохранят свою структуру и числовые форматы.

Для автоматизации передачи результатов в другие системы используйте функцию WriteExcel. Она позволяет напрямую записывать значения переменных в файл Excel по заданному пути. Синтаксис: WriteExcel("путь\файл.xlsx", "лист", "ячейка", переменная).

Чтобы сохранить численные значения в виде текстовых файлов, используйте функцию WRITEPRN("файл.txt", переменная). Результат сохраняется построчно без форматирования, что удобно для последующего импорта в программное обеспечение анализа данных.

Mathcad также поддерживает сохранение графиков в виде изображений. Щелкните по графику, затем используйте контекстное меню и выберите «Сохранить как изображение». Поддерживаются форматы PNG и BMP с сохранением разрешения и цветовой палитры.

Регулярно сохраняйте рабочие файлы в формате .mcdx или .xmcd, чтобы избежать потери данных. Рекомендуется включить автосохранение через «Файл» → «Параметры» → «Сохранение» и задать интервал не более 5 минут.

Вопрос-ответ:

Можно ли в Mathcad решать уравнения с параметрами, а не только числовые?

Да, Mathcad позволяет решать уравнения с параметрами. Если переменные не заданы конкретными числами, они остаются символьными, и результатом решения будет выражение, зависящее от этих параметров. Для символьного решения применяется команда `solve`, предваряемая оператором символьного расчета (`→`). Например, при вводе уравнения `a·x + b = 0` и команды `solve(x) →`, Mathcad выразит `x` через `a` и `b`, если это возможно.

Есть ли в Mathcad способ проверить, имеет ли уравнение несколько решений?

Mathcad сам по себе не ищет все возможные решения уравнения, особенно если используется функция `find`. Она возвращает только одно решение, зависящее от начального приближения. Чтобы исследовать наличие нескольких корней, можно задавать разные начальные приближения и повторять вычисления. Кроме того, для символьного анализа можно использовать функцию `roots` или экспортировать уравнение в другой математический пакет, если требуется полный набор решений.

Как задать неравенство в Mathcad и решить его?

Mathcad ограниченно работает с неравенствами. Численное решение неравенств напрямую невозможно, но символьные преобразования доступны. Например, можно записать выражение `solve, x^2 — 4 < 0`, и при использовании символьного расчета (`→`) Mathcad вернет область значений `x`, при которых выполняется неравенство. Однако, стоит учитывать, что символьное решение работает корректно только при простых неравенствах и выражениях. Сложные случаи требуют пошагового анализа или использования дополнительного программного обеспечения.