Как решить уравнение в mathcad prime

Mathcad Prime позволяет решать алгебраические и дифференциальные уравнения с минимальным количеством ручных вычислений. Интерфейс ориентирован на инженерные задачи, а логика записи максимально приближена к математической нотации. Решение уравнений возможно как численно, так и аналитически, с сохранением промежуточных шагов.

Чтобы решить уравнение f(x) = 0, необходимо определить переменную, задать выражение и применить встроенную функцию solve или оператор root. Например, уравнение x² − 5x + 6 = 0 вводится как символьное выражение, после чего используется команда solve, x, которая возвращает корни уравнения в виде списка. Для численного решения применяется root(f(x), x, x₀), где x₀ – начальное приближение.

Системы уравнений оформляются в виде векторных уравнений с использованием оператора двойного двоеточия := и ключевого слова find. Например, система из двух уравнений с переменными x и y оформляется как набор выражений, объединённых в вектор, и решается через find(x, y). Все переменные предварительно инициализируются либо оставляются неопределёнными для символьной обработки.

При работе с дифференциальными уравнениями используются операторы производной и численные методы, такие как Odesolve. Уравнение второго порядка предварительно представляется в виде системы первого порядка, с введением вспомогательных переменных. Решение отображается в виде графика или массива значений, в зависимости от цели расчёта.

Для отладки решения важно контролировать единицы измерения, так как Mathcad Prime учитывает размерности автоматически. Ошибки в системе единиц могут привести к некорректным результатам или отказу вычисления. Использование комментариев и пошаговых проверок выражений помогает сохранить читаемость и управляемость проекта.

Настройка единиц измерения перед решением уравнения

Перед вводом уравнения в Mathcad Prime необходимо задать корректные единицы измерения, чтобы избежать ошибок интерпретации физических величин. Mathcad Prime автоматически отслеживает размерности, поэтому несогласованные единицы вызовут предупреждение или приведут к неверному результату.

Для установки системы единиц перейдите во вкладку Math и в группе Units выберите Unit System. Доступны системы: SI, USCS, CGS и Custom. Например, для инженерных расчётов чаще всего используется SI (метры, килограммы, секунды).

При вводе чисел всегда указывайте единицу явно. Пример: v := 72 km/h. Mathcad автоматически преобразует эту величину к базовой единице в выбранной системе (в данном случае – м/с).

Чтобы увидеть текущие единицы результата, используйте команду форматирования: щёлкните по выражению правой кнопкой мыши, выберите Unit Display и задайте нужное отображение, например, m/s, kW или N·m.

Для изменения единицы у результата уравнения без пересчёта значения используйте символ подстановки единицы, например:

E := m * g * h
E ⇒ kJ

В этом случае Mathcad выполнит пересчёт энергии E в килоджоули. Следите, чтобы подставляемая единица была совместима по размерности – программа проверит это автоматически.

Если требуется использовать пользовательские единицы, создайте их через определение, например: 1 atm := 101.325 kPa. После этого atm станет доступной во всех расчётах.

Ввод алгебраических уравнений в рабочее поле

Для ввода уравнения в Mathcad Prime активируйте рабочее поле щелчком мыши и сразу начинайте печатать выражение. Переменные набираются латиницей, знаки операций вводятся с клавиатуры: «+» для сложения, «-» для вычитания, «*» для умножения, «/» для деления. Для возведения в степень используйте клавишу «^», например, x^2.

Уравнение задаётся с использованием символа равенства «=». Если необходимо ввести выражение как уравнение для решения, используйте символ двойного равенства «=» (вводится через клавишу «Ctrl» + «=»). Это указывает Mathcad, что вы работаете с уравнением, а не присваиваете значение.

Корректная структура важна: каждая переменная должна быть определена или использоваться в пределах известного контекста. Mathcad не интерпретирует ввод как в алгебраической записи на бумаге – выражения необходимо набирать в точной логической последовательности.

Для группировки используйте круглые скобки «( )». При вводе дробей предпочтительно использовать горизонтальный дробный формат, активируемый клавишей «Ctrl» + «/», что облегчает визуальное восприятие сложных выражений.

Если уравнение содержит функции, используйте встроенные обозначения: например, «sqrt(x)» для корня, «sin(x)» для синуса. При вводе функций убедитесь, что аргументы указаны в скобках, иначе Mathcad может интерпретировать запись некорректно.

Для систем уравнений каждый элемент вводится на новой строке, а затем используется функция solve или lsolve для поиска решения. Не объединяйте уравнения в одну строку – это приведёт к синтаксической ошибке.

Проверяйте статус выражения: если оно подсвечено красным, это означает синтаксическую или логическую ошибку. Наведите курсор, чтобы увидеть описание проблемы и внести исправления.

Использование функции solve для нахождения неизвестного

Функция solve в Mathcad Prime предназначена для алгебраического решения уравнений относительно одной переменной. Она применяется внутри блока solve block, который обязательно должен включать инструкции Given и уравнение или систему уравнений.

Для начала создаётся блок решения: введите Given, затем запишите уравнение, где переменная остаётся неизвестной. После этого используйте solve(variable) для нахождения значения.

Пример. Требуется найти значение x из уравнения 3·x + 2 = 11. Последовательность действий:

1. Вставьте Given

2. Запишите: 3·x + 2 = 11

3. Ниже: x := solve(x)

Mathcad автоматически выполнит символическое решение и подставит результат в переменную x. Если в уравнении несколько решений, будет возвращён только один (по умолчанию – аналитически допустимый). Для получения всех возможных решений следует использовать find в числовом контексте или применять дополнительные условия.

Функция solve применяется только к символьным выражениям. Перед использованием убедитесь, что переменные не определены численно выше по листу – это может нарушить корректность решения.

Для повышения точности решения рекомендуется избегать дробей с плавающей точкой в уравнениях. Вместо 0.333 используйте 1/3 – это обеспечит символическое представление и правильное решение уравнения.

Если уравнение содержит параметры, не имеющие значений, Mathcad выразит неизвестное через них. Это полезно при работе с формулами общего вида.

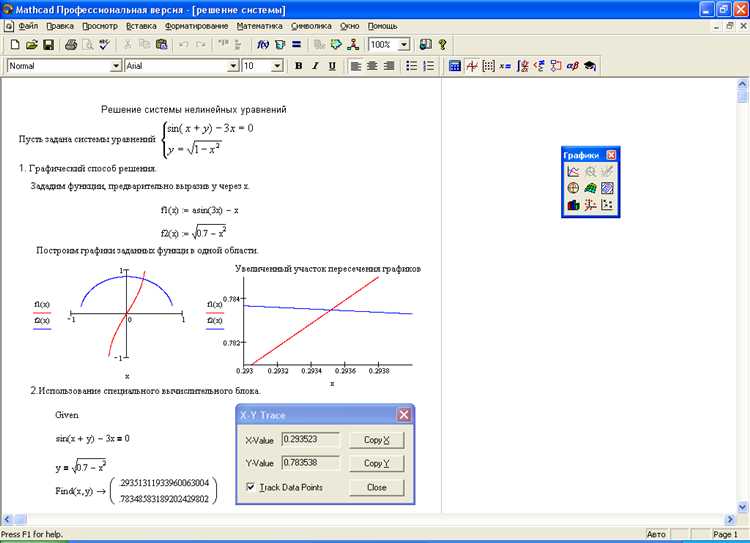
Применение оператора Given для систем уравнений

Оператор Given в Mathcad Prime позволяет задавать систему уравнений как совокупность условий, которую необходимо решить. Для этого используется конструкция, в которой последовательно записываются уравнения, затем применяется функция find с перечислением искомых переменных в круглых скобках.

Каждое уравнение должно быть записано с использованием логического оператора равенства =, а не присваивания :=. После оператора Given можно указывать как алгебраические, так и трансцендентные уравнения, включая ограничения на переменные.

Пример: необходимо решить систему уравнений:

x + y = 10
x - y = 4

В Mathcad Prime это записывается следующим образом:

Given
x + y = 10
x - y = 4
find(x, y)

Результатом выполнения будет численное решение переменных x и y. Mathcad автоматически применяет численные методы для получения корней. Для уравнений с несколькими решениями find возвращает одно из возможных значений, зависящее от начальных приближений, которые можно задать через guess values.

Если система содержит нелинейные уравнения, рекомендуется предварительно задать начальные приближения в виде выражений x := 1, y := 1 до оператора Given. Это повышает вероятность нахождения корректного решения и снижает риск ошибок типа «no solution found».

Оператор Given особенно полезен при решении задач с параметрами, когда уравнения зависят от внешних переменных. В этом случае можно использовать встроенные функции и производные значения в теле системы.

В отличие от символьного решателя, find работает только с числовыми значениями, поэтому переменные и параметры должны иметь численные определения. Для символьного анализа применяется solve, но он не использует Given.

Определение начальных приближений при численном решении

Начальные приближения критически влияют на сходимость численных методов в Mathcad Prime, особенно при использовании итерационных алгоритмов, таких как метод Ньютона или секущих. Неверно выбранное приближение может привести к расходимости или попаданию в ложный корень.

Для выбора начального приближения следует проанализировать график функции. В Mathcad Prime удобно использовать функцию plot для построения графика на заданном интервале. Например, чтобы визуально определить корень уравнения f(x) = x^3 - 5x + 1 в диапазоне [-3; 3], необходимо:

x := -3, -2.9 .. 3
f(x) := x^3 - 5·x + 1
plot(x, f(x))

Если график показывает пересечение оси абсцисс в точке около x = -2, то это и есть разумное начальное приближение.

При отсутствии точной информации о поведении функции можно использовать производную для оценки кривизны. В Mathcad Prime вычисляется производная через встроенный оператор:

f′(x) := d/dx(f(x), x)

Если |f′(x₀)| близка к нулю, метод Ньютона теряет эффективность – следует изменить x₀ или использовать другой метод.

Для систем нелинейных уравнений начальные приближения должны учитывать масштаб каждой переменной. В Mathcad Prime следует нормировать переменные или задать начальные значения вручную в виде вектора:

x₀ := [1; -0.5; 2]

Желательно избегать симметричных начальных точек в многоэкстремальных задачах, так как это может привести к сходимости к нежелательному решению. В таких случаях рекомендуется проводить анализ функции на участках с разными начальными условиями и сравнивать полученные корни.

Итерационные методы в Mathcad Prime, такие как root, позволяют задавать интервал поиска корня. В этом случае начальные приближения задаются в виде границ интервала, и важно обеспечить изменение знака функции на концах:

root(f(x), x = a..b)

Если f(a)·f(b) > 0, Mathcad выдаст ошибку – необходимо корректировать границы.

Решение уравнений с параметрами и переменными

В Mathcad Prime уравнения с параметрами и переменными решаются с использованием встроенных функций и операторов, обеспечивающих точность и гибкость при работе с разными типами данных.

1. Объявите параметры и переменные, задав им конкретные числовые значения или диапазоны для анализа. Например: a := 3, x – переменная без фиксированного значения.
2. Запишите уравнение с параметрами в явном виде, используя символы = или := для присвоения. Mathcad Prime автоматически распознает зависимые переменные и параметры.
3. Для численного решения используйте функцию root(), указав уравнение и переменную. Например: root(x^2 + a*x - 5, x) вычислит корни относительно x при заданном параметре a.
4. Если необходимо исследовать влияние параметров, создайте диапазон значений с помощью оператора диапазона: a := 1, 2..10, затем используйте векторизацию функции root() для автоматического расчета корней при каждом значении параметра.
5. Для систем уравнений с несколькими переменными и параметрами используйте функцию Find(), задавая массив уравнений и список переменных. Параметры должны быть определены заранее.
6. Проверяйте корректность решения с помощью графиков, построенных через функцию plot(), где параметры меняются по оси, а переменные – по другой, что позволяет визуально оценить зависимость и выявить нестабильные области.

Основные рекомендации:

• Объявляйте параметры до задания уравнений для предотвращения ошибок вычислений.
• Используйте явное обозначение переменных и параметров для облегчения чтения и последующего редактирования документа.
• Проверяйте размерность и типы данных параметров, особенно при использовании векторов или матриц.
• При работе с несколькими параметрами группируйте расчёты по блокам, чтобы избежать путаницы.
• Используйте встроенные функции проверки решений, такие как подстановка найденных корней обратно в уравнения для контроля точности.

• Символьное решение формируется с помощью функции solve() или встроенных операторов символьной алгебры. При этом результат сохраняет переменные, корни уравнений, параметры в аналитическом выражении.
• Если уравнение имеет несколько корней, Mathcad Prime вернёт их в виде множества символов или параметрических выражений без приближений.

• Численное решение получают применением функции numeric() или автоматическим вычислением выражения, если оно содержит только числовые данные.
• Для повышения точности численных результатов задайте желаемую точность с помощью функции precision() или через параметры документа.
• В случаях с нелинейными уравнениями используйте численные методы типа FindRoot(), где важно указать начальное приближение для стабильного и быстрого сходимости решения.

1. Чтобы сравнить символьное и численное решение, введите уравнение, затем рядом выведите его символьный корень (symbolic()) и численное значение (numeric()).
2. Проверяйте корректность символьных выражений, подставляя числовые значения параметров для выявления возможных ошибок или неопределённостей.

Такой подход позволяет обеспечить наглядность и точность в анализе решений, минимизировать ошибки, связанные с округлениями или неправильным пониманием формата результата.

Обработка ошибок при решении уравнений в Mathcad Prime

Ошибки синтаксиса выявляются сразу при вводе уравнения и сопровождаются подсветкой ошибок и сообщениями системы. Для их устранения нужно проверить правильность использования операторов, функций и переменных, а также соблюдение скобочной структуры. Mathcad Prime строго реагирует на опечатки в именах функций и переменных.

Ошибка «No Solution Found» возникает, когда численный решатель не может найти корень в заданном диапазоне. Для её устранения рекомендуется изменить интервал поиска или уточнить начальное приближение. При системах уравнений полезно проверить корректность всех уравнений и отсутствие конфликтующих условий.

Проблемы с условием сходимости появляются, если метод решения не подходит для конкретного типа уравнения. В таких случаях стоит использовать альтернативные функции Mathcad Prime, например, Root() с указанием метода решения, или прибегнуть к аналитическим преобразованиям для упрощения уравнения.

При обработке ошибок важно разделять типы уравнений: линейные решаются встроенной функцией solve(), а для нелинейных лучше применять find() с тщательно подобранными параметрами. Отслеживание промежуточных значений и графический анализ функции помогают выявить причины отсутствия решения.

Если уравнение содержит параметры, их диапазоны следует ограничивать явно, чтобы избежать выхода за допустимые значения. Также полезно использовать встроенные функции валидации данных, чтобы минимизировать влияние ошибочных входных данных.

Для сложных систем уравнений рекомендуется разбивать задачу на этапы и проверять решение по частям. Это позволяет быстро локализовать ошибку и исправить её без полной перестройки модели.

Вопрос-ответ:

Как в Mathcad Prime задать уравнение для решения?

В Mathcad Prime уравнение задаётся с помощью знака равенства, например, f(x) := выражение, а затем уравнивается к значению, например, f(x) = 0. Важно, чтобы переменная была определена или объявлена, после чего можно применять функции решения. Уравнение вводится прямо на рабочем листе, и Mathcad распознаёт его как математическое выражение.

Какие методы решения уравнений доступны в Mathcad Prime?

Mathcad Prime предоставляет несколько методов для поиска корней уравнений. Основной из них — численное решение с помощью функции Root. Она позволяет указать уравнение и начальное приближение для поиска корня. Также можно использовать функции для систем уравнений и уравнений с несколькими переменными. Для некоторых простых уравнений возможно аналитическое решение, но чаще применяется численный подход.

Как правильно использовать функцию Root для решения уравнения с одной переменной?

Функция Root принимает в качестве аргументов выражение уравнения, переменную и начальное значение для поиска решения. Например, Root(f(x), x, x0), где f(x) — выражение, x — переменная, x0 — стартовое приближение. После вычисления Root возвращает значение переменной, при котором уравнение обращается в ноль. Важно выбирать начальное значение близко к ожидаемому корню, чтобы обеспечить сходимость решения.

Можно ли в Mathcad Prime решать системы уравнений и как это сделать?

Да, Mathcad Prime позволяет решать системы уравнений с несколькими переменными. Для этого обычно используют функцию Root или встроенные средства численного решения, задавая систему в виде вектора функций, равных нулю. Каждой переменной соответствует уравнение, а в качестве начальных значений задаётся вектор начальных приближений. После запуска вычисления Mathcad возвращает вектор решений, который удовлетворяет системе.

Какие ошибки могут возникнуть при решении уравнений в Mathcad Prime и как их избежать?

Часто встречаются ошибки, связанные с неправильным вводом уравнений, отсутствием начальных приближений или неправильным указанием переменных. Ещё одна причина — неподходящая функция для типа уравнения. Чтобы минимизировать ошибки, следует проверять правильность записи выражений, использовать понятные имена переменных, выбирать корректные начальные значения и внимательно следить за синтаксисом функций. При численных методах важно понимать, что решение может не сойтись, если начальное приближение далеко от корня.

Как шаг за шагом задать уравнение для решения в Mathcad Prime?

Для начала в Mathcad Prime нужно создать область вычислений и вписать уравнение с использованием стандартного синтаксиса. Например, для уравнения вида \(x^2 + 3x — 4 = 0\) введите его как выражение, присвоив левую часть функции, а затем используйте встроенную функцию решения, такую как `solve`. Далее укажите переменную, которую нужно найти. Mathcad автоматически преобразует уравнение и выдаст корни. Каждый шаг можно визуально контролировать, вводя промежуточные выражения и наблюдая их результаты.