Как решить дифференциальное уравнение в mathcad

Mathcad предоставляет встроенные инструменты для численного и аналитического решения дифференциальных уравнений, что значительно ускоряет процесс моделирования и анализа систем. В первую очередь важно правильно задать уравнение в формате, понятном программе: уравнения вводятся с помощью функции dsolve или оператора ODE для систем уравнений. При этом ключевым этапом является точное определение начальных условий, без которых корректное вычисление невозможно.

Для решения задачи необходимо выбрать подходящий метод интегрирования, доступный в Mathcad: метод Эйлера, Рунге-Кутты или встроенные адаптивные схемы. В процессе настройки стоит учитывать точность и скорость расчета, задавая параметры шага интегрирования через свойства функций. Рекомендуется сначала проводить тестовые прогоны на упрощенных уравнениях, чтобы оценить стабильность выбранного метода.

После получения численного решения результат визуализируется с помощью графиков, что позволяет сразу выявить критические точки и проверить адекватность модели. Mathcad поддерживает построение графиков зависимости переменных по времени, что облегчает интерпретацию динамических процессов. Для автоматизации решения в сложных задачах можно использовать циклы и условные операторы, интегрируя этапы вычислений в единую структуру.

Подготовка среды Mathcad для работы с дифференциальными уравнениями

Для эффективного решения дифференциальных уравнений в Mathcad необходимо корректно настроить рабочее пространство и проверить основные параметры программы.

Версия Mathcad: убедитесь, что используется версия Mathcad Prime 5.0 или выше, поскольку она содержит расширенные инструменты для работы с ОДУ и ПДУ.

Объявление переменных: перед вводом уравнений задайте начальные условия и параметры в виде числовых значений или функций. Mathcad распознаёт их как скалярные, векторные или матричные переменные, что критично для корректного вычисления.

Использование встроенных функций: подключите встроенные операторы решения дифференциальных уравнений, такие как rkfixed (метод Рунге-Кутты), или odesolve. Для этого достаточно использовать контекстную панель функций и выбрать подходящий метод.

Настройка области определения: задайте диапазон независимой переменной (например, времени) с точным шагом. Неправильное определение области и шага может привести к ошибкам вычислений или неустойчивому решению.

Резервное копирование: создайте шаблон рабочего листа с типовыми настройками для дифференциальных уравнений, что позволит ускорить подготовку к последующим вычислениям и исключить типовые ошибки.

Определение и ввод начальных условий в Mathcad

Для решения дифференциальных уравнений в Mathcad необходимо задать начальные условия, определяющие значение функции и её производных в конкретной точке.

1. Выберите переменную независимой величины, например x, и функцию, например y(x).
2. Определите уравнение, используя оператор производной Mathcad: для первой производной – y', для второй – y''.
3. Для задания начальных условий используйте выражения вида: y(x0) = y0, y'(x0) = y1, где x0 – точка, в которой задаются условия, y0 и y1 – численные значения.
4. Начальные условия необходимо ввести отдельно и в явном виде до запуска функции решения, чтобы Mathcad корректно их распознал.
5. Для систем дифференциальных уравнений аналогично задаются начальные значения каждой функции и её производных.

Пример ввода начальных условий:

• x0 := 0
• y(x0) := 2
• y'(x0) := -1

Далее, при использовании функции решения, например rkfixed или odesolve, укажите эти начальные значения в аргументах. Это обеспечивает корректное построение численного решения с нужной точкой отсчёта.

Использование встроенных функций для решения ОДУ первого порядка

В Mathcad для решения обыкновенных дифференциальных уравнений (ОДУ) первого порядка применяется функция rkfixed – реализация метода Рунге-Кутты фиксированного шага. Она обеспечивает точное численное решение при заданных начальных условиях.

Формат вызова функции: rkfixed(уравнение, переменная, начальное_значение, интервал_решения, шаг). В уравнении переменная и её производная должны быть выражены в виде функции, например, y'(x) = f(x,y). Начальное значение задается как значение функции при начальной точке.

Для корректной работы рекомендуется придерживаться шага интегрирования, не превышающего 0.1 для уравнений с быстро меняющимися решениями. В противном случае возможны значительные ошибки и расхождение численного решения.

Кроме rkfixed, используется функция ode – более универсальный инструмент с автоматическим подбором шага и контролем погрешности. Ее синтаксис: ode(уравнение, переменная, начальное_значение, интервал_решения). Внутренние алгоритмы оптимизируют вычисления для повышения точности.

В обоих случаях для задания уравнения в Mathcad применяется оператор производной '. Например, уравнение dy/dx = -2*y + x записывается как y'(x) := -2*y(x) + x. Обязательно указывать область определения переменной и начальное значение функции.

При анализе результата рекомендуется строить график полученного решения с помощью стандартных инструментов Mathcad и сравнивать с аналитическим решением при возможности. Это поможет выявить ошибки в постановке задачи и подобрать оптимальный шаг интегрирования.

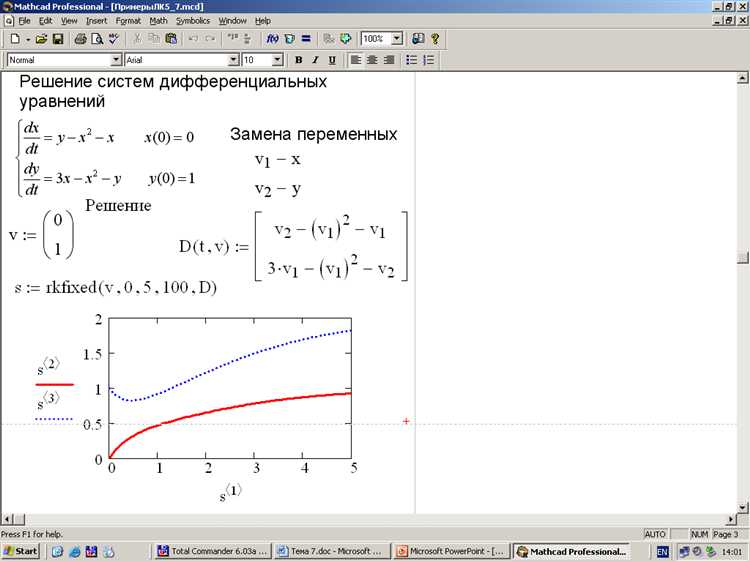
Методы решения систем дифференциальных уравнений в Mathcad

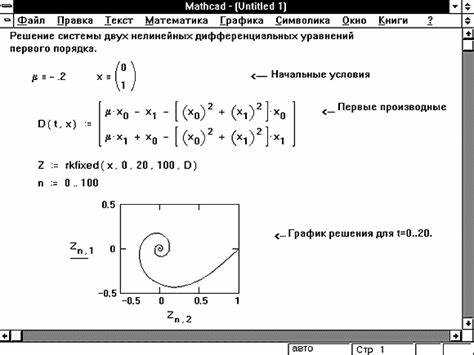
Для решения систем дифференциальных уравнений в Mathcad применяют численные методы, встроенные в функции интегрирования. Основной инструмент – функция rkfixed и rk45, реализующие методы Рунге-Кутты с фиксированным и адаптивным шагом соответственно.

Систему уравнений задают в виде векторной функции, возвращающей производные по каждой переменной. Затем указывают начальные условия как вектор начальных значений и интервал интегрирования. Формат вызова функции интегрирования: rk45(функция, начальное значение, интервал).

Метод Рунге-Кутты 4-5 порядка (rk45) предпочтителен при необходимости балансировки точности и вычислительных затрат. Для жёстких систем применяют ode15s – специализированный алгоритм, доступный в расширенных пакетах Mathcad.

Обязательное условие корректной работы – корректное определение функции, описывающей систему, с использованием векторов и явным возвратом всех производных в одном выражении. Ошибки в размере или порядке возвращаемого вектора ведут к сбоям вычислений.

Для анализа результатов удобно использовать встроенные инструменты построения графиков, задавая отдельные функции из вектора решений. При необходимости повышения точности настраивают шаг интегрирования, уменьшая интервал или используя адаптивные методы.

Построение графиков решений дифференциальных уравнений в Mathcad

Для построения графика решения дифференциального уравнения в Mathcad необходимо сначала определить функцию решения с помощью встроенных средств численного интегрирования, например, оператора ode или функции rkfix.

После получения численного решения задайте интервал переменной, обычно с помощью оператора диапазона, например: x := 0, 0.1 .. 10. Затем вычислите значения решения на этом интервале, подставляя каждый элемент x в функцию решения.

Построение графика осуществляется командой графика из панели инструментов Mathcad. В качестве аргументов укажите вектор значений x и соответствующий вектор значений функции y. Для точного отображения кривой рекомендуется использовать плотный шаг по x – не более 0.01 при гладких решениях.

Если уравнение задаётся системой, строят графики каждого компонента решения отдельно, используя одинаковый интервал и настройки осей. Для сравнения нескольких решений применяйте функцию наложения графиков, задавая разные цвета или стили линий через свойства графика.

Для улучшения визуализации можно добавить подписи осей, заголовки, и сетку. Mathcad поддерживает динамическое обновление графиков при изменении параметров уравнения или начальных условий, что позволяет оперативно анализировать влияние изменений.

Настройка параметров численного интегрирования и точности

В Mathcad для численного решения дифференциальных уравнений важно корректно задавать параметры интегрирования, чтобы обеспечить баланс между скоростью вычислений и точностью результата. Основные параметры, влияющие на качество численного решения, включают шаг интегрирования, метод интегрирования и критерии остановки.

Шаг интегрирования задается в аргументе функции интегратора. Его уменьшение повышает точность, но увеличивает время вычислений. Рекомендуется начинать с шага, равного одной сотой от интервала интегрирования, и по необходимости уменьшать его, если наблюдаются значительные ошибки или нестабильность решения.

Mathcad предлагает несколько методов интегрирования, например, Рунге-Кутта 4-го порядка (RK4) и адаптивные методы. Для задач с резкими изменениями решения предпочтительнее использовать адаптивные алгоритмы, которые динамически изменяют шаг на основе оценки локальной погрешности.

Для контроля точности численного решения в Mathcad задаются параметры абсолютной и относительной погрешности. Значения в диапазоне 10^-6–10^-9 обычно обеспечивают достаточную точность для инженерных задач. При необходимости более высокой точности эти параметры можно уменьшить, но это увеличит время вычислений.

При настройке параметров важно тестировать решение на граничных значениях шага и погрешности, чтобы убедиться в устойчивости и корректности результата. В случае расхождений между аналитическим и численным решением следует уменьшить шаг интегрирования или повысить точность погрешности.

Кроме того, Mathcad позволяет вручную задавать максимальное количество шагов интегрирования, чтобы избежать бесконечных циклов при сложных уравнениях. Рекомендуется выставлять это значение с запасом, например, в 2–3 раза превышающим ожидаемое количество шагов.

Итоговая рекомендация: оптимальная настройка начинается с выбора метода RK4, шага около 0.01 интервала, относительной и абсолютной погрешности около 10^-7, и контролем максимального количества шагов. После первичного запуска стоит провести адаптацию параметров в зависимости от поведения решения и специфики задачи.

Обработка ошибок и отладка расчетов дифференциальных уравнений

В Mathcad ошибки при решении дифференциальных уравнений чаще всего связаны с некорректными начальными условиями, неверным определением функций или неподходящими методами численного интегрирования. Для эффективной отладки расчетов необходимо систематически проверять ключевые элементы модели.

1. Проверка определения уравнения и начальных условий

   • Убедитесь, что уравнение записано в форме, совместимой с выбранным решателем (обычно y’ = f(x,y)).
   • Начальные условия должны строго соответствовать переменным и быть заданы в одной точке.
   • Проверьте единицы измерения и масштаб переменных – несоответствие вызывает ошибочные решения или неустойчивость.

2. Выбор метода численного решения

   • Mathcad поддерживает разные алгоритмы: Эйлера, Рунге-Кутты, Адамса. Для жестких уравнений используйте методы с адаптивным шагом.
   • Сравните результаты при разных методах и параметрах шага – резкие расхождения сигнализируют о нестабильности или ошибках в постановке задачи.

3. Анализ и диагностика ошибок

   • Используйте встроенные функции для отображения промежуточных значений переменных и результатов на каждом шаге (например, создание массивов для отслеживания динамики решения).

4. Пошаговая отладка

   • Разбейте уравнение на части и проверяйте их отдельно, например, определение функции правой части уравнения.
   • Выполните тестовые вычисления с упрощенными параметрами для выявления некорректных значений.
   • Используйте визуализацию: графики функций и производных помогают выявить аномалии и резкие скачки в решении.

5. Улучшение стабильности расчетов

   • Уменьшайте шаг интегрирования до тех пор, пока решение не перестанет изменяться качественно.
   • При наличии жесткости используйте специализированные методы или переходите к более устойчивым численным схемам.
   • Контролируйте диапазон переменных, избегайте выхода за пределы области определения функции.

Регулярное применение этих подходов позволяет минимизировать ошибки и повысить надежность расчетов дифференциальных уравнений в Mathcad.

Экспорт и сохранение результатов решения дифференциальных уравнений

В Mathcad результаты решения дифференциальных уравнений можно сохранять в нескольких форматах. Для экспорта численных данных рекомендуется использовать формат CSV. Для этого выделите массив или вектор решения, кликните правой кнопкой мыши и выберите пункт «Сохранить как». В открывшемся окне укажите формат CSV и путь для сохранения. При этом сохраняются только численные значения без форматирования и графиков.

Для сохранения графиков, отображающих поведение решения, используйте экспорт в формат изображения (PNG или JPG). Щёлкните правой кнопкой по графику, выберите «Сохранить изображение как» и укажите нужный формат. Разрешение изображения напрямую зависит от размеров графика в рабочем окне, поэтому рекомендуется увеличить его перед экспортом.

Если необходимо передать все расчёты вместе с графиками и аннотациями, используйте экспорт в PDF. Откройте меню «Файл» → «Печать» → выберите «Печать в PDF». Это создаёт точную копию рабочей области, включая все выражения и пояснения.

Для автоматизированной обработки решений другими системами (например, MATLAB или Python) удобен экспорт в формате XML или XSLX. Используйте команды writeexcel или writetext, задав путь и имя файла, а также переменные, подлежащие экспорту. Следует предварительно очистить данные от лишних символьных элементов, чтобы избежать ошибок при импорте.

Рекомендуется сохранять промежуточные результаты в отдельные файлы, особенно при работе с параметрическими или многозадачными моделями. Это снижает риск потери данных и упрощает отладку модели.

Вопрос-ответ: