Как решить систему линейных уравнений в matlab

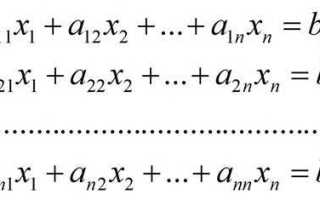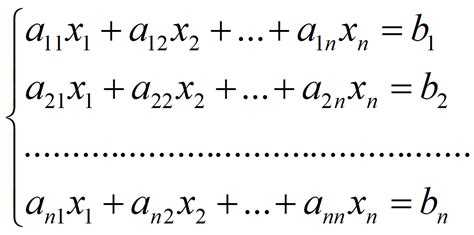
MATLAB предоставляет мощный инструментарий для решения систем линейных уравнений различной сложности. Основной способ – использование оператора обратной косой черты \, который реализует эффективные численные алгоритмы в зависимости от свойств матрицы коэффициентов. Например, при решении выражения A \ b, MATLAB автоматически определяет наилучший метод: LU-разложение для квадратных матриц, QR-разложение для прямоугольных и псевдообратную матрицу при наличии несовместной системы.

Прямая инверсия матрицы через функцию inv() не рекомендуется из-за численной нестабильности и меньшей производительности. Вместо x = inv(A) * b следует использовать x = A \ b, что уменьшает погрешности округления и ускоряет вычисления. Для разреженных матриц можно использовать тип sparse, что значительно снижает объем потребляемой памяти и ускоряет выполнение операций.

Для анализа корректности решения MATLAB предлагает функции cond() и rcond() для оценки обусловленности матрицы. Значение, близкое к нулю, указывает на потенциальные проблемы с точностью решения. В таких случаях рекомендуется использовать метод наименьших квадратов или сингулярное разложение (svd()) при помощи функции pinv().

Создание коэффициентной матрицы и вектора правых частей

Для решения системы линейных уравнений вида Ax = b в MATLAB необходимо явно задать матрицу коэффициентов A и вектор свободных членов b. Размерность A должна быть m×n, где m – число уравнений, а n – число переменных. Вектор b должен иметь размер m×1.

Определите матрицу A как двумерный массив с использованием квадратных скобок и точек с запятой:

В MATLAB решение системы линейных уравнений вида AX = B с использованием обратной матрицы осуществляется по формуле X = inv(A) * B. Однако такой подход оправдан только в случае, если матрица A невырожденная и хорошо обусловлена.

Перед применением оператора inv() необходимо убедиться, что определитель матрицы A не равен нулю: det(A) ~= 0. Использование inv() при сингулярной или почти сингулярной матрице приводит к значительным численным погрешностям.

Для минимизации ошибок важно проверять число обусловленности: cond(A). Если cond(A) > 10^10, применение обратной матрицы не рекомендуется. В таких случаях предпочтительнее использовать встроенный оператор обратного слэша: X = A \ B, который более устойчив к численным погрешностям.

Также не следует использовать inv(A)*B в итерационных расчетах или при работе с разреженными матрицами. Оператор inv() требует полного хранения всех элементов, что увеличивает вычислительные и ресурсные затраты.

Если всё же необходимо явно получить обратную матрицу, например, для аналитического анализа, используйте inv() только после предварительной оценки состояния матрицы A. Для повышения точности можно использовать двойную точность: A = double(A).

Использование функции linsolve для прямого решения

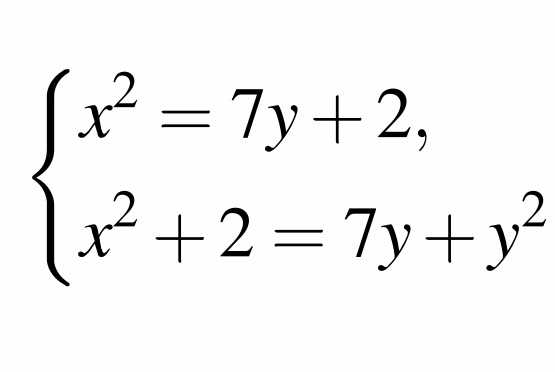
Функция linsolve в MATLAB предназначена для прямого решения систем линейных уравнений вида AX = B, где A – квадратная или прямоугольная матрица коэффициентов, B – правая часть. В отличие от оператора обратной матрицы или функции inv, linsolve использует оптимальные алгоритмы, адаптированные под свойства матрицы.

• Базовый синтаксис: X = linsolve(A, B).
• Если известны свойства матрицы A, рекомендуется использовать опцию opts для повышения эффективности.
• Пример с симметричной положительно определённой матрицей:

  opts.SYM = true;
  opts.POSDEF = true;
  X = linsolve(A, B, opts);
  

• Преимущества:
  • Избегает ненужного вычисления обратной матрицы.
  • Автоматически выбирает LU, QR или Cholesky разложение в зависимости от структуры A.
  • Подходит для плохо обусловленных систем при наличии информации о разреженности и симметрии.
• Рекомендации:
  • Перед использованием linsolve проверьте тип и свойства матрицы с помощью issymmetric, cond, issparse.
  • Для сильно разреженных матриц используйте sparse(A) перед передачей в linsolve.
  • Избегайте использования inv(A)*B, если linsolve или A\B дают тот же результат – это быстрее и численно устойчивее.

Использование linsolve предпочтительно, когда известны характеристики матрицы A – это позволяет MATLAB выбрать наиболее эффективный алгоритм решения.

Проверка существования и единственности решения

В MATLAB для проверки существования и единственности решения системы линейных уравнений Ax = b необходимо анализировать ранг матрицы A и расширенной матрицы [A b]. Используйте функцию rank():

rA = rank(A);
rAb = rank([A b]);

Если rA ≠ rAb, система несовместна и решения не существует. Если rA = rAb = n, где n – число неизвестных, то решение единственно. Если rA = rAb < n, существует бесконечно много решений.

Для квадратной матрицы также можно использовать определитель: det(A). Если он равен нулю, система может быть несовместной или иметь бесконечно много решений. Если определитель отличен от нуля, решение единственно.

Проверку можно автоматизировать:

if rank(A) == rank([A b])
if rank(A) == size(A,2)
disp('Система имеет единственное решение');
else
disp('Система имеет бесконечно много решений');
end
else
disp('Система не имеет решений');
end

Для устойчивого анализа предпочтительно избегать det(), так как при вычислениях с плавающей точкой он менее надёжен. Используйте rank() и cond() для оценки вырожденности:

cond(A) даёт численную оценку обусловленности. Значения значительно превышающие 1e10 указывают на потенциальную нестабильность и чувствительность решения к малым изменениям в данных.

Решение переопределённых и недоопределённых систем

Переопределённые системы содержат больше уравнений, чем переменных. В MATLAB такие системы, как правило, решаются методом наименьших квадратов. Используйте оператор обратного слэша \:

x = A \ b;

где A – матрица размера m×n с m > n, b – столбец правых частей. MATLAB возвращает вектор x, минимизирующий норму невязки ||Ax — b||. Для получения всех решений при сингулярной A применяйте pinv(A)*b, где pinv – псевдообратная по Муру-Пенроузу.

Недоопределённые системы имеют меньше уравнений, чем переменных. Решения в этом случае не единственные. MATLAB возвращает базисное решение, если использовать x = A \ b при m < n. Чтобы найти решение минимальной нормы, применяйте:

x = pinv(A) * b;

Для контроля над степенью свободы используйте null(A) – функция возвращает базис пространства решений однородной системы Ax = 0. Общее решение представляется как:

x_general = x_particular + null(A)*c;

где c – произвольный вектор. При наличии дополнительных критериев оптимизации, используйте lsqlin из Optimization Toolbox.

Работа с комплексными коэффициентами в уравнениях

Для решения систем линейных уравнений с комплексными коэффициентами в MATLAB используется тот же синтаксис, что и для вещественных, но с учетом особенностей комплексных чисел. Матрица коэффициентов A и вектор свободных членов b могут содержать элементы с действительной и мнимой частью, задаваемые через оператор i или j. Например:

A = [2+3i, 4-2i; 1-i, 5+0i];

b = [1+2i; 3-4i];

Для нахождения решения системы A*x = b применяется стандартная команда x = A\b;. MATLAB корректно обрабатывает комплексные значения, учитывая как действительную, так и мнимую части при вычислениях.

При работе с комплексными системами важно убедиться в невырожденности матрицы коэффициентов. Определитель для комплексной матрицы можно проверить командой det(A). Если модуль определителя близок к нулю, решение может быть неустойчивым.

Для повышения точности в сложных задачах рекомендуется использовать функции, учитывающие особенности комплексных чисел, например, linsolve с опцией ‘RECT’ или QR-разложение через qr. Также возможно применение функции cond(A) для оценки обусловленности системы, что особенно важно при наличии близких по значению комплексных коэффициентов.

real_part = real(x);
imag_part = imag(x);

В случае необходимости можно визуализировать комплексные решения на комплексной плоскости с помощью функции plot(real(x), imag(x), 'o').

Вопрос-ответ:

Как в MATLAB можно решить систему линейных уравнений с несколькими неизвестными?

Для решения системы линейных уравнений в MATLAB используется оператор обратной косой черты «\». Например, если система записана в виде Ax = b, где A — матрица коэффициентов, а b — вектор свободных членов, то решение находится командой x = A \ b. Этот способ более устойчив численно по сравнению с вычислением обратной матрицы.

Можно ли решить систему уравнений с помощью функции linsolve в MATLAB и чем она отличается от использования оператора «\»?

Да, функция linsolve также предназначена для решения линейных систем. Она позволяет задать дополнительные параметры, учитывающие свойства матрицы A, например, симметричность или разреженность. В таких случаях linsolve может работать быстрее или точнее. Однако для большинства задач оператор «\» является универсальным и простым решением.

Как проверить, существует ли решение у системы линейных уравнений в MATLAB?

Одним из способов проверки является вычисление ранга матрицы коэффициентов и расширенной матрицы, которая включает столбец свободных членов. Если ранги совпадают и равны числу неизвестных, система имеет единственное решение. В MATLAB это можно сделать с помощью команды rank(A) и rank([A b]). Также можно проверить детерминант матрицы A — если он равен нулю, решение может отсутствовать или быть бесконечным множеством.

Что делать, если система уравнений плохо обусловлена или матрица коэффициентов вырождена?

Если матрица коэффициентов близка к вырожденной, решение системы становится нестабильным, и небольшие ошибки в данных сильно влияют на результат. В таких случаях рекомендуют использовать методы регуляризации или функции, специально предназначенные для работы с вырожденными матрицами, например, псевдообратную через pinv. MATLAB позволяет вычислить псевдообратную матрицы и получить минимально нормальное решение системы.