Как решить уравнение в matlab

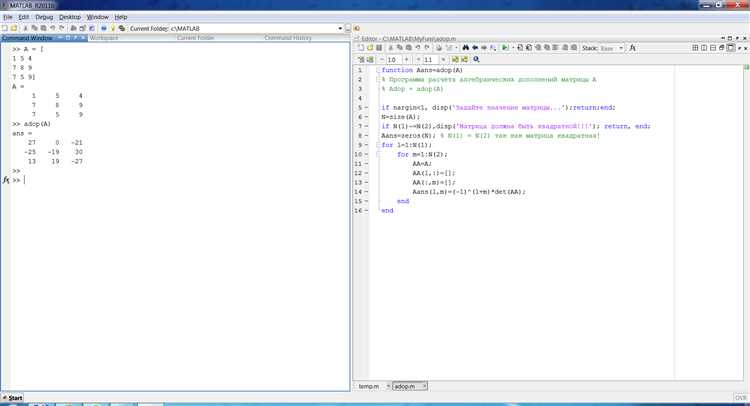
MATLAB предоставляет широкий инструментарий для численного и аналитического решения уравнений. Встроенные функции solve и fsolve позволяют находить как точные, так и приближённые корни, при этом пользователь может управлять точностью, начальными условиями и способом решения. Этот материал содержит конкретные пошаговые инструкции по работе с линейными, нелинейными и системами уравнений в MATLAB без лишней теории и с упором на практическое применение.

Для численного решения используется fsolve() из пакета Optimization Toolbox. Эта функция применима для сложных нелинейных уравнений, где аналитическое решение невозможно. Например, уравнение cos(x) = x можно решить с помощью анонимной функции и вызова fsolve(@(x) cos(x) — x, 0.5). Начальное приближение критично: результат и скорость сходимости зависят от его выбора. Для систем уравнений создаются векторные функции, а решение вызывается аналогично.

Как решать линейные уравнения с одной переменной с помощью команды solve

Для решения линейного уравнения вида ax + b = 0 в MATLAB необходимо использовать символьные переменные и функцию solve. Начните с объявления переменной:

syms x

Далее задайте уравнение в символьной форме. Например, уравнение 3x - 9 = 0 записывается так:

eq = 3*x - 9 == 0;

Для получения решения используйте команду:

sol = solve(eq, x);

Результат сохраняется в переменной sol. Он будет символьным выражением, равным корню уравнения. Для численного значения можно воспользоваться функцией double:

double(sol)

Если коэффициенты выражаются переменными, например a*x + b == 0, решение также будет символьным:

syms x a b
sol = solve(a*x + b == 0, x);

Результат – выражение -b/a, что полезно при аналитических преобразованиях.

Пример решения системы линейных уравнений с использованием матриц и оператора \

Рассмотрим систему уравнений:

2x + 3y — z = 5

4x — y + 5z = 10

-6x + 2y + 2z = -1

В MATLAB сначала задаём матрицу коэффициентов и вектор свободных членов:


A = [2 3 -1; 4 -1 5; -6 2 2];
b = [5; 10; -1];


Для решения используем оператор обратного деления:


x = A\b;


Результат сохраняется в векторе x, содержащем значения неизвестных x, y и z. Команда disp(x) выведет ответ на экран. Оператор \ автоматически применяет метод Гаусса с оптимизацией по численной устойчивости. Он предпочтительнее явного вычисления обратной матрицы: inv(A)*b менее точен и менее эффективен по ресурсам.

Перед решением рекомендуется проверить, является ли матрица A невырожденной. Используем:


det_A = det(A);


Если det_A ≠ 0, решение существует и единственно. При det_A = 0 необходимо дополнительно исследовать совместность и степень свободы решений.

Решение нелинейного уравнения одной переменной через fsolve

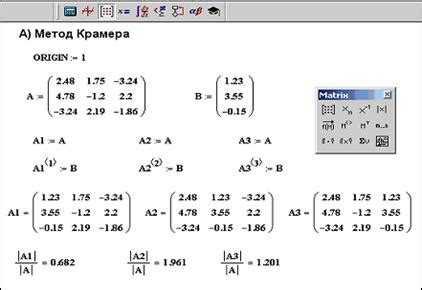
Функция fsolve в MATLAB применяется для численного решения нелинейных уравнений вида f(x) = 0. Она требует начального приближения и чувствительна к его выбору. Функция входит в пакет Optimization Toolbox.

1. Определите функцию. Создайте анонимную функцию или отдельный файл:

   f = @(x) x.^3 - 5*x + 1;

2. Укажите начальное приближение:

   x0 = 2;

   Рекомендуется анализировать график функции перед выбором точки старта:

   fplot(f, [-10, 10]); grid on;

3. Вызовите fsolve:

   x = fsolve(f, x0);

   disp(x);

4. Настройте параметры через optimoptions при необходимости:

   opts = optimoptions('fsolve', 'Display', 'iter', 'TolFun', 1e-8);
   x = fsolve(f, x0, opts);

• Если корень не находится, проверьте производную или смените x0.
• Для многокорневых уравнений используйте разные x0 и анализируйте график функции.
• Если функция не определена в какой-то области, избегайте этих участков при выборе начального приближения.

Функция fsolve не гарантирует нахождение глобального корня – только локального при заданном x0. Контроль результатов обязателен.

Настройка начальных приближений и опций для fsolve

Функция fsolve требует точного задания начального приближения. От него зависит, сойдётся ли метод Ньютона к корню и какой именно корень будет найден при наличии нескольких решений. Используйте максимально приближённое значение, основанное на графике функции или физическом смысле задачи. Например, для уравнения exp(x) - 2 = 0 хорошим приближением будет x0 = 1, так как exp(1) ≈ 2.718.

Начальное приближение задаётся как аргумент x0 при вызове fsolve:
x = fsolve(@myfun, x0);

Для систем уравнений x0 должен быть вектором с тем же числом элементов, что и количество уравнений:
x0 = [1; -1; 0];

Точные настройки управления решением определяются с помощью функции optimoptions. Чтобы контролировать алгоритм, число итераций и точность, используйте:

opts = optimoptions('fsolve', 'Display', 'iter', 'Algorithm', 'trust-region-dogleg', 'FunctionTolerance', 1e-8, 'StepTolerance', 1e-10, 'MaxIterations', 100);

Ключевые параметры:

• 'Algorithm' – выбор алгоритма; для гладких задач предпочтителен 'trust-region-dogleg', для жёстких – 'levenberg-marquardt'.
• 'FunctionTolerance' – абсолютная погрешность по значению функции; уменьшение значения повышает точность.
• 'StepTolerance' – порог изменения переменной между итерациями; используется для остановки.
• 'MaxIterations' – ограничение числа итераций; полезно для предотвращения зацикливания.

Вызов fsolve с опциями осуществляется так:
x = fsolve(@myfun, x0, opts);

Для отладки используйте 'OutputFcn' и 'PlotFcns' для визуального контроля процесса. Например:

opts = optimoptions('fsolve', 'PlotFcns', {@optimplotx, @optimplotfval});

Корректно подобранные начальные значения и параметры optimoptions существенно повышают надёжность и точность нахождения корней уравнений.

Использование syms для символьного решения уравнений

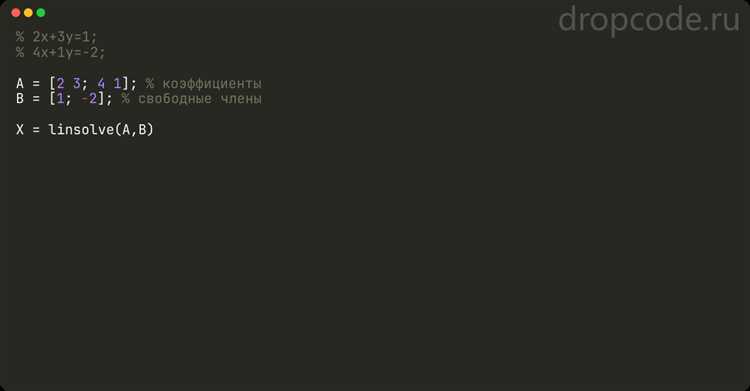
Функция syms объявляет символьные переменные, необходимые для аналитического решения уравнений. Например, syms x создаёт символьную переменную x, которую можно использовать в выражениях и уравнениях без предварительного задания числового значения.

Для решения уравнений применяется функция solve. Конструкция solve(x^2 - 4 == 0, x) возвращает точные корни: -2 и 2. Второй аргумент указывает переменную, относительно которой ведётся решение. Без него MATLAB решает относительно всех символьных переменных в уравнении.

Система уравнений передаётся в solve в виде массива. Пример: syms x y; solve([x + y == 3, x - y == 1], [x, y]). Результатом будет структура с полями x и y, содержащими точные значения переменных.

Чтобы получить решение в виде массива, используют синтаксис [xSol, ySol] = solve(...). Это упрощает последующую работу с решениями, особенно в численных расчётах.

Для получения численного значения символьного результата применяют double() или vpa(). Первая выдаёт приближённое значение в двойной точности, вторая – с произвольной точностью, например: vpa(sqrt(2), 10).

Если уравнение содержит параметры, solve возвращает решение в общем виде. Пример: syms a x; solve(a*x == 1, x) даст 1/a. Это полезно при аналитических преобразованиях и построении универсальных моделей.

Построение графика уравнения для визуального анализа корней

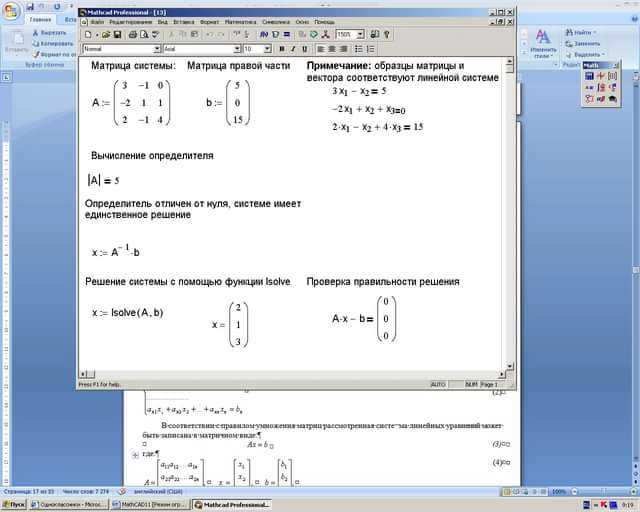
Для наглядного определения корней уравнения в MATLAB оптимально использовать построение графика функции. Это позволяет быстро выявить интервалы, где функция меняет знак, что указывает на наличие корней.

1. Определите функцию, например, через анонимную функцию:
   f = @(x) x.^3 - 6*x.^2 + 11*x - 6;
2. Выберите диапазон для построения графика, охватывающий предполагаемые корни. Например:
   x = linspace(0, 4, 400);
3. Постройте график с помощью команды:
   plot(x, f(x)); grid on;
4. Добавьте горизонтальную линию y=0 для визуального контроля пересечений:
   hold on; plot(x, zeros(size(x)), '--k'); hold off;
5. Используйте zoom и pan для детального изучения участков, где график пересекает ось X.

При визуальном анализе обращайте внимание на участки, где функция меняет знак – там находятся корни. Для более точного определения используйте функции fzero с начальными приближениями, полученными из графика.

Решение уравнений с параметрами и подстановка значений

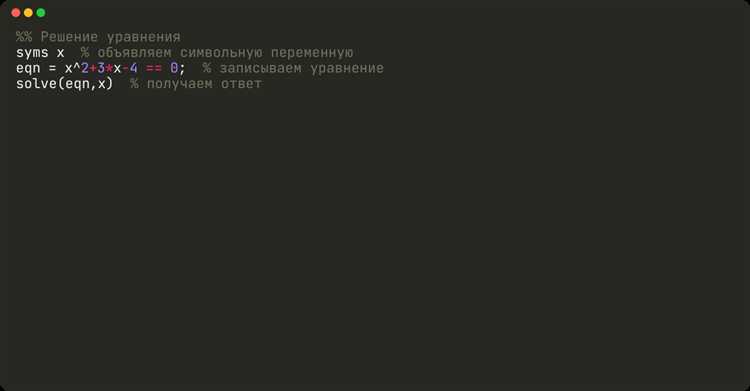
В MATLAB для работы с уравнениями, содержащими параметры, используют символьные переменные и функцию solve. Параметры объявляют через syms, например: syms x a b. После этого уравнение записывается как символьное выражение, например, eq = a*x^2 + b*x + 1 == 0.

Для решения уравнения по переменной x при произвольных параметрах достаточно вызвать solve(eq, x). Результат будет зависеть от параметров a и b, предоставляя общее аналитическое решение.

Чтобы подставить конкретные числовые значения параметров, используется функция subs. Например, чтобы заменить a = 2, b = -3, нужно вызвать eq_num = subs(eq, [a, b], [2, -3]). Полученное уравнение можно затем решить численно или аналитически.

Если требуется численное значение корней, после подстановки параметров удобно применить double к результату solve, чтобы получить числовые значения. Пример: sol = double(solve(eq_num, x)).

В случае нескольких уравнений с параметрами используют систему символов и передают их списком: eqs = [a*x + b == 0, x + y == c], где параметры a, b, c можно заменить через subs перед решением.

Рекомендация: перед подстановкой параметров проверяйте вид решения без них, чтобы понять зависимость и избежать деления на ноль или недопустимых значений. Также полезно использовать assume для задания ограничений на параметры, что помогает MATLAB корректно трактовать решения.

Диагностика и обработка ошибок при решении уравнений в MATLAB

При решении уравнений в MATLAB ошибки чаще всего возникают из-за некорректного задания функций, неправильного выбора начальных приближений или несоответствия типа уравнения используемому методу. Для диагностики используйте функцию lastwarn, которая возвращает последнее предупреждение, и try-catch конструкции для перехвата исключений.

Если функция решения, например fsolve, не сходится, проверьте значение выходного параметра exitflag. Значение exitflag < 1 означает, что решение не найдено – в таком случае стоит изменить начальное приближение или проанализировать поведение целевой функции на графике.

Ошибки, связанные с нечисловыми значениями или NaN, указывают на синтаксические или математические ошибки в определении уравнения. Используйте debugger MATLAB, устанавливая точки останова на вычислениях функции, чтобы проследить промежуточные результаты.

Вопрос-ответ:

Как в MATLAB задать и решить простое алгебраическое уравнение?

Для решения уравнения в MATLAB сначала необходимо задать переменную как символьную с помощью функции `syms`. Затем уравнение записывают в виде выражения с равенством к нулю. Например, чтобы решить уравнение \(x^2 — 4 = 0\), пишут: `syms x`, `eq = x^2 — 4 == 0;`, после чего вызывают функцию `solve(eq, x)`. Результатом будет набор корней уравнения.

Какие функции MATLAB помогают анализировать решения уравнений, например, получить только действительные корни?

После получения всех корней с помощью `solve`, можно использовать функцию `double` для перевода символьных значений в числовой формат. Чтобы выделить только действительные корни, применяют функцию `isreal` к результатам. Также можно использовать параметр `’Real’, true` в функции `solve`, который ограничит поиск только реальными решениями. Таким образом, отсеивание комплексных корней становится удобным и быстрым.

Как решать уравнения с параметрами в MATLAB, и как получить выражение решения в символическом виде?

Если в уравнении присутствуют параметры, их также нужно определить как символьные переменные с помощью `syms`. Например, для уравнения \(a x^2 + b x + c = 0\) нужно написать: `syms x a b c`. Далее уравнение задается: `eq = a*x^2 + b*x + c == 0;`. Вызов `solve(eq, x)` вернет решение в общем виде через параметры. Это удобно, если требуется исследовать влияние параметров на корни.

Можно ли автоматизировать процесс решения уравнений в MATLAB для большого количества уравнений или систем?

Да, для серии уравнений можно использовать циклы или функции. Например, если у вас много похожих уравнений с разными коэффициентами, создайте массивы коэффициентов и в цикле формируйте уравнения, решая каждое с помощью `solve`. Результаты удобно сохранять в ячейки или структуры. Такой подход позволяет быстро получать решения для множества случаев без ручного ввода каждого уравнения.