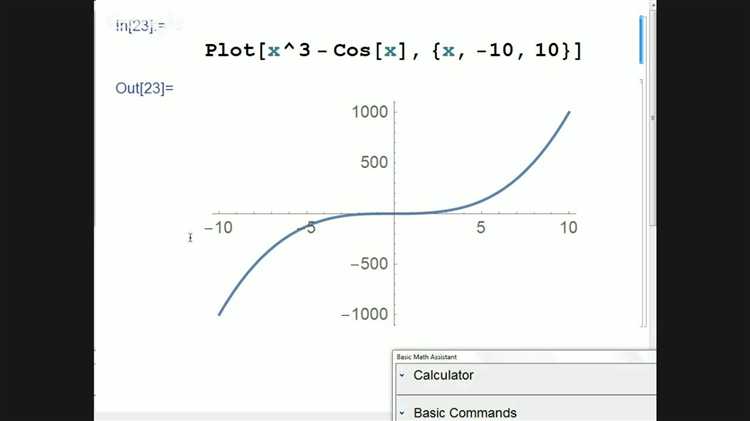
Wolfram Mathematica предоставляет широкий набор инструментов для аналитического и численного решения уравнений. Ключевая функция Solve применяется для точного алгебраического решения, включая системы линейных и нелинейных уравнений. Например, запрос Solve[x^2 — 4 == 0, x] мгновенно возвращает корни x = -2 и x = 2.
Для уравнений, не имеющих точного решения в элементарных функциях, используется функция NSolve для численного поиска корней. Если уравнение включает трансцендентные функции, такие как синус, экспонента или логарифм, применяется FindRoot с указанием начального приближения: FindRoot[Sin[x] — x/2 == 0, {x, 1}].
В отличие от многих систем компьютерной алгебры, Mathematica автоматически обрабатывает уравнения с параметрами, возвращая обобщённые решения. Например, Solve[a x + b == 0, x] выдаст x = -b/a, при условии a ≠ 0. Уточнение условий осуществляется через Assumptions или функцию Reduce, которая анализирует множество всех допустимых решений и возвращает их в логической форме.
Для систем уравнений с несколькими переменными Mathematica обеспечивает мощные методы символьной элиминации, включая Eliminate и GroebnerBasis. Это позволяет решать системы даже с нелинейной зависимостью переменных, что делает платформу эффективной при работе с задачами из алгебры, геометрии и прикладной математики.
Как решить алгебраическое уравнение с одной переменной

Для решения алгебраического уравнения с одной переменной в Wolfram Mathematica используется функция Solve. Например, чтобы найти корни уравнения \( x^2 — 5x + 6 = 0 \), введите:
Solve[x^2 - 5 x + 6 == 0, x]
Результатом будет список правил подстановки: {{x -> 2}, {x -> 3}}. Это означает, что уравнение имеет два корня: \( x = 2 \) и \( x = 3 \).
Если уравнение не имеет рациональных корней, Mathematica все равно вернёт точный результат. Например:
Solve[x^2 - 2 == 0, x]
даст {{x -> -Sqrt[2]}, {x -> Sqrt[2]}}, что соответствует \( x = \pm\sqrt{2} \).
Для получения численных приближений используйте N:
N[Solve[x^2 - 2 == 0, x]]
Результат: {{x -> -1.41421}, {x -> 1.41421}}.
Если необходимо получить только одно решение, применяйте FindRoot. Например:
FindRoot[x^3 - x - 1 == 0, {x, 1}]
возвращает приближённое значение действительного корня, начиная с начального приближения \( x = 1 \).
Для многочленов высокой степени используйте Reduce, чтобы получить полную информацию о корнях и условиях существования решений:
Reduce[x^5 - x == 0, x]
возвращает x == 0 || x == -1 || x == 1, отображая все действительные и комплексные корни, если они есть.
Что делать, если уравнение содержит корни и дроби

При наличии корней и дробей в уравнении необходимо особое внимание уделить преобразованиям, чтобы избежать ошибок при решении. В Wolfram Mathematica наиболее эффективно использовать функции Simplify, Together, PowerExpand и FullSimplify перед применением Solve или Reduce.
Если уравнение включает дроби, следует привести выражения к общему знаменателю при помощи Together[expr]. Это упрощает структуру уравнения и помогает Mathematica правильно интерпретировать структуру выражения:
Together[(1/x) + (1/(x + 1))]Корни (например, квадратные или кубические) требуют осторожного обращения, так как они могут вводить посторонние решения при возведении в степень. Для безопасного устранения корней используйте PowerExpand только при уверенности в допустимости алгебраических преобразований (оно может игнорировать ограничения знаков):
PowerExpand[Sqrt[x^2]]Для уравнений, содержащих как корни, так и дроби, рекомендуется следующий порядок действий:
- Упростите выражение с помощью
Together. - Если возможно, используйте
FullSimplifyдля автоматической рационализации. - Примените
SolveилиReduceдля поиска решений.
Пример: решить уравнение (1/Sqrt[x]) + (1/(x - 1)) == 2:
Solve[(1/Sqrt[x]) + (1/(x - 1)) == 2, x]Если решение содержит условия на область допустимых значений, Mathematica их отразит явно. Для контроля области определения вручную используйте Assuming или Reduce:
Reduce[(1/Sqrt[x]) + (1/(x - 1)) == 2 && x > 0 && x ≠ 1, x]Также полезно проверять решения на посторонние корни, особенно если в процессе использовалось возведение в степень. Для этого можно использовать подстановку найденных значений в исходное уравнение:
Chop[expr /. x -> sol]Такой подход позволяет минимизировать ошибки и контролировать точность при работе с уравнениями, содержащими как корни, так и дробные выражения.
Как найти все действительные и комплексные корни уравнения
Для нахождения всех корней уравнения в Wolfram Mathematica используйте функции Solve и NSolve в зависимости от типа уравнения и необходимости в точных или численных решениях.
Solve[eq, x]– находит аналитические решения уравненияeqотносительно переменнойx. Работает для уравнений, выражаемых через элементарные функции.NSolve[eq, x]– вычисляет все численные корни (включая комплексные) при условии, что коэффициенты – точные (например, целые или рациональные числа).N[Solve[eq, x]]– сначала ищет точные решения, затем переводит их в численную форму.
Если уравнение имеет несколько переменных, используйте форму Solve[{eq1, eq2}, {x, y}]. Для поиска только действительных корней добавьте ограничение:
Solve[{eq, x ∈ Reals}, x]Для получения только комплексных корней можно фильтровать результаты:
Select[Solve[eq, x], !Element[x /. #, Reals] &]Чтобы уточнить количество корней и их природу, применяйте:
Reduce[eq, x]– показывает условия существования решений и их вид.Roots[poly == 0, x]– для уравнений с рациональными коэффициентами, выдаёт факторизованную форму.
Для многочленов используйте:
NSolve[x^5 - 3 x^3 + 2 == 0, x]Для трансцендентных уравнений – только FindRoot, но она требует начального приближения и даёт одно решение:
FindRoot[Sin[x] - x/2 == 0, {x, 1}]Если важны все корни уравнения с вещественными и комплексными значениями, оптимальный подход – NSolve или Solve с последующей фильтрацией по типу корней.
Чем отличается использование Solve и Reduce
Solve применяется для получения конкретных решений уравнений или систем уравнений. Возвращает список подстановок, пригодных для непосредственного использования в вычислениях или подстановке. Пример: Solve[x^2 == 4, x] выдаёт {{x -> -2}, {x -> 2}}.
Reduce анализирует множество решений глубже. Возвращает логическое выражение, описывающее всё множество решений, включая условия существования. Пример: Reduce[a x == 1, x] вернёт a ≠ 0 && x == 1/a, указывая условие применимости решения.
Solve не всегда сообщает об ограничениях на параметры. При параметрических уравнениях может вернуть частичные или неполные решения. Reduce в таких случаях даёт полную характеристику множества решений с явным указанием условий.
Для систем уравнений с логическими ограничениями Reduce предпочтительнее. Например, Reduce[{x^2 == y, y > 0}, {x, y}] даст точное описание зависимостей между переменными, а Solve может возвратить неполный список решений.
Используйте Solve, если требуется получить конкретные численные или символьные значения переменных. Выбирайте Reduce, когда важна полная логическая структура решений, включая условия на параметры и переменные.
Как задать систему уравнений и получить её решения
Для задания системы уравнений в Wolfram Mathematica используйте списки и функцию Solve или NSolve в зависимости от типа решений (аналитические или численные).
- Система записывается в виде списка уравнений:
{eq1, eq2, ..., eqn}. - Переменные также указываются списком:
{x, y, ...}. - Для точных решений используйте
Solve, для приближённых –NSolve.
Пример: решение линейной системы
Solve[{2 x + 3 y == 7, x - y == 1}, {x, y}]Пример с численным решением:
NSolve[{Sin[x] + y == 1, x^2 + y^2 == 4}, {x, y}]Если переменных больше, чем уравнений, Mathematica возвращает общее решение с параметрами:
Solve[{x + y == 5}, {x, y}]Для систем с неявными ограничениями используйте Reduce:
Reduce[{x^2 + y^2 == 1, x y > 0}, {x, y}]Чтобы получить одно конкретное решение из множества возможных, используйте FindInstance:
FindInstance[{x^2 + y^2 == 1, x > 0, y > 0}, {x, y}, Reals]Для систем с параметрами задавайте их явно и используйте Assumptions, если нужно уточнить область определения:
Solve[{a x + y == 1, x - y == a}, {x, y}]Какие методы применимы к трансцендентным уравнениям

Для решения трансцендентных уравнений в Wolfram Mathematica применяются численные методы и аналитические подходы с использованием специальных функций. К численным методам относятся функции FindRoot и NSolve, которые позволяют находить приближённые корни с заданной точностью. FindRoot эффективен при наличии начального приближения и поддерживает различные алгоритмы, включая метод Ньютона и секущих.
В случаях, когда уравнение включает стандартные специальные функции (например, тригонометрические, экспоненциальные, логарифмы, Бесселя или гипергеометрические функции), Mathematica может использовать встроенные возможности упрощения и преобразования, а также применять функцию Reduce для анализа условий существования решений.
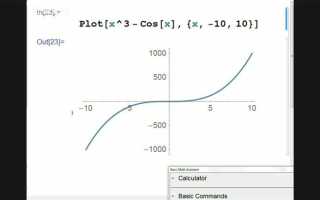
Для сложных уравнений, которые невозможно выразить аналитически, полезно использовать метод обхода корней через графический анализ с помощью Plot, чтобы выбрать стартовые значения для FindRoot. Оптимально задавать опцию WorkingPrecision для повышения точности и MaxIterations для контроля вычислительного процесса.
Если уравнение зависит от параметров, эффективен параметрический анализ с функциями Manipulate или Table для выявления поведения корней при изменении параметров. В ряде случаев возможно использование функции Root для задания корней через алгебраические уравнения, что облегчает работу с аналитическими представлениями.
Таким образом, для трансцендентных уравнений в Mathematica предпочтительны численные методы с точным управлением параметрами вычислений и комбинирование их с аналитическими преобразованиями и визуализацией, что позволяет добиться оптимального баланса между скоростью и точностью решения.
Как ограничить область поиска решений
В Wolfram Mathematica область поиска решений уравнения можно ограничить с помощью дополнительных условий или диапазонов переменных. Для численных методов оптимально использовать параметры Method и WorkingPrecision, а также задавать начальные приближения.
Для функции FindRoot рекомендуется указывать точку старта и явно задавать диапазон переменной через условие: FindRoot[f[x] == 0 && a ≤ x ≤ b, {x, x0} ]. Это гарантирует, что корень будет найден именно в интервале [a, b].
При использовании NSolve или Reduce можно добавить ограничивающие неравенства в систему: NSolve[{eqn, a ≤ x ≤ b}, x]. Это позволяет получить решения только в указанном диапазоне.
В аналитических решениях через Solve ограничение вводится дополнительным условием, что уменьшает число неподходящих корней: Solve[{eqn, a ≤ x ≤ b}, x].
Для уравнений с несколькими переменными области ограничиваются аналогично, указывая условия для каждой переменной, например: Solve[{eqn, a ≤ x ≤ b, c ≤ y ≤ d}, {x, y}].
Также полезно использовать параметр Assumptions в функциях, где он поддерживается, чтобы ограничить тип решений (например, только действительные или положительные).
Как отобразить решения уравнения графически

Пример для уравнения f[x] = 0: сначала найдите корни с помощью Solve или NSolve, затем используйте Plot, чтобы построить график f[x] на заданном интервале. Для отметки корней добавьте ListPlot с координатами {корень, 0}.
Для уравнений с двумя переменными вида f[x, y] = 0 применяйте ContourPlot с уровнем ноль. Например, ContourPlot[f[x, y] == 0, {x, xmin, xmax}, {y, ymin, ymax}] покажет множество точек (x, y), удовлетворяющих уравнению.
Чтобы улучшить читаемость, используйте опции PlotStyle для изменения цвета и толщины линий, а также Epilog для добавления меток или дополнительных графических элементов на график.
Для сложных уравнений можно использовать RegionPlot, который выделяет область решения, если она существует, или ParametricPlot при параметрическом виде решений.
Важный прием – комбинировать графики с помощью Show, чтобы визуализировать несколько решений или сравнить функции на одном изображении.
Вопрос-ответ:
Как в Wolfram Mathematica решить уравнение с одной переменной?
Для решения уравнения с одной переменной в Wolfram Mathematica используется функция Solve. Например, чтобы найти корни уравнения x^2 — 4 == 0, можно выполнить команду Solve[x^2 — 4 == 0, x]. Результатом будет список правил вида {{x -> 2}, {x -> -2}}, которые показывают найденные значения переменной.
Можно ли в Mathematica решать системы нелинейных уравнений? Как это сделать?
Да, Mathematica позволяет решать системы нелинейных уравнений. Для этого также используется функция Solve, но в ней нужно указать список уравнений и список переменных. Например, чтобы решить систему: {x^2 + y^2 == 1, x — y == 0}, вводят Solve[{x^2 + y^2 == 1, x — y == 0}, {x, y}]. Результатом будет список решений, удовлетворяющих обоим уравнениям.
Какие существуют альтернативы Solve для решения уравнений в Mathematica, и в каких случаях их лучше использовать?
Помимо Solve, в Mathematica есть функция NSolve, которая находит численные приближённые решения уравнений, а также FindRoot — метод для поиска корней, если известна приблизительная точка. NSolve хорошо подходит для уравнений с конечным числом решений, когда нужно получить числовые значения, а FindRoot применяют для уравнений, решение которых сложно получить аналитически. Кроме того, Reduce позволяет получить более подробное описание множества решений, включая условия на параметры.
Как задать ограничения на переменные при решении уравнений в Mathematica?
Чтобы ввести ограничения на переменные, например, требование, что переменная должна быть действительным числом, можно использовать функцию Reduce или дополнительно указать условия в Solve с помощью логических выражений. Например, Solve[{x^2 == 4, x > 0}, x] вернёт только положительный корень. В Reduce можно использовать такие же условия, при этом результат будет включать все допустимые значения с учётом ограничений.
Можно ли в Mathematica решить дифференциальное уравнение, и если да, то как это сделать?
Да, Mathematica предназначена для решения дифференциальных уравнений. Для этого существует функция DSolve, которая находит аналитическое решение. Например, чтобы решить уравнение y'[x] == y[x], нужно написать DSolve[y'[x] == y[x], y[x], x]. В ответе будет выражение, содержащее общее решение с интеграционной константой. Для численного решения используют функцию NDSolve.
Какие функции в Wolfram Mathematica лучше всего подходят для решения алгебраических уравнений?
Для решения алгебраических уравнений в Wolfram Mathematica широко используются функции Solve и NSolve. Solve позволяет получить точные аналитические решения для уравнений с одной или несколькими переменными. Если уравнение слишком сложное для аналитического решения или требуется численное приближение, тогда применяют NSolve. Кроме того, существует функция Reduce, которая не просто решает уравнение, а даёт полное описание множества решений с учётом условий переменных. Выбор функции зависит от типа уравнения и требуемого результата.
Как в Mathematica можно решать дифференциальные уравнения и какие особенности стоит учитывать при этом?
Для решения дифференциальных уравнений в Mathematica обычно используют функцию DSolve, которая предназначена для получения аналитических решений. Если аналитическое решение невозможно, применяют NDSolve, дающую численное приближение. Важно правильно задать уравнение и начальные или граничные условия — это влияет на корректность и полноту ответа. Также стоит учитывать, что сложные уравнения могут приводить к громоздким выражениям, и в таких случаях полезно упростить результат с помощью функций упрощения. Для численных решений можно настраивать параметры точности и диапазон интегрирования, чтобы получить более стабильный результат.