Как решить задачу коши в maple

Задача Коши для обыкновенных дифференциальных уравнений задаётся в виде уравнения с начальными условиями: y'(x) = f(x, y), y(x₀) = y₀. В среде Maple её можно решить аналитически и численно, используя встроенные функции dsolve и numeric. Правильное использование этих инструментов позволяет получать точные или приближённые решения с минимальными затратами времени.

Для аналитического решения необходимо задать дифференциальное уравнение в виде выражения, используя команду dsolve({уравнение, начальные условия}, y(x)). Например, чтобы решить уравнение y’ = y + x при y(0) = 1, в Maple следует записать: dsolve({diff(y(x), x) = y(x) + x, y(0) = 1}, y(x)).

Если аналитическое решение невозможно или не требуется, можно воспользоваться численным методом. Для этого к команде dsolve добавляется параметр numeric. Результатом будет процедура, которую можно вызывать для вычисления значений функции при различных x. Пример: sol := dsolve({diff(y(x), x) = y(x) + x, y(0) = 1}, y(x), numeric), затем sol(1.5) вернёт значение решения в точке x = 1.5.

Для визуализации решения используется команда plots[odeplot], позволяющая построить график на заданном интервале. Это особенно полезно при анализе поведения решения и оценке устойчивости. В связке с численным решением применяется следующий синтаксис: plots[odeplot](sol, [x, y(x)], x = 0..5).

Точная формулировка задачи, корректный синтаксис команд и грамотный выбор метода решения – ключевые факторы успешного применения Maple к задачам Коши. Каждый из этапов требует внимания к деталям: от ввода уравнения до анализа графика полученного решения.

Постановка задачи Коши и выбор начальных условий

Задача Коши формулируется как начальная задача для обыкновенного дифференциального уравнения первого порядка: необходимо найти функцию $ y(x) $, удовлетворяющую уравнению $ y’ = f(x, y) $ и начальному условию $ y(x_0) = y_0 $. В Maple эта задача задаётся через команду dsolve с указанием уравнения и начального условия в виде списка.

Перед вводом уравнения следует явно определить зависимость функции от переменной: например, $ y = y(x) $. Это критично для корректной обработки Maple. Пример: dsolve({diff(y(x), x) = sin(x + y(x)), y(0) = 1}, y(x)).

Выбор начальной точки $ x_0 $ и значения $ y_0 $ должен учитывать особенности функции $ f(x, y) $. При наличии особенностей или разрывов в окрестности точки $ x_0 $ численные методы Maple могут дать неверный результат или не сработать вовсе. Следует предварительно исследовать область определения функции $ f(x, y) $ аналитически или с помощью команды plot3d.

Если планируется численное решение, например методом Эйлера или Рунге-Кутты, важно задать значения $ x_0 $ и $ y_0 $, находящиеся в области, где функция непрерывна и допускает дифференцирование. Также следует заранее оценить допустимую длину шага интегрирования, чтобы избежать накопления ошибки.

Для систем уравнений начальные условия задаются для каждой функции отдельно. Пример для системы: dsolve({diff(y1(x), x) = y2(x), diff(y2(x), x) = -y1(x), y1(0) = 0, y2(0) = 1}, {y1(x), y2(x)}).

Ввод дифференциального уравнения в синтаксисе Maple

Для задания обыкновенного дифференциального уравнения в Maple необходимо использовать встроенную функцию diff. Пример уравнения второго порядка: diff(y(x), x$2) + 3*diff(y(x), x) + 2*y(x) = 0. Здесь x$2 означает вторую производную по x, diff(y(x), x) – первую производную, y(x) – функция.

Перед вводом уравнения подключите пакет DEtools или dsolve, используя команду with(DEtools): или with(PDEtools):. Это обеспечит доступ к функциям упрощения и решения.

Если необходимо задать уравнение в виде выражения, а не равенства, используйте оператор = для преобразования: eq := diff(y(x), x$2) + y(x) = sin(x);. Это позволит далее использовать dsolve(eq, y(x)).

Для систем уравнений используйте список: eq1 := diff(y(x), x) = z(x); eq2 := diff(z(x), x) = -y(x); dsolve({eq1, eq2}, {y(x), z(x)});.

Именование переменных чувствительно к регистру. y(x) и Y(x) – разные функции. Соблюдайте единый стиль обозначений во всём решении.

Использование команды dsolve для численного решения

Для численного решения задачи Коши в Maple используется команда dsolve с параметром numeric. Исходное уравнение задаётся в виде уравнения, а начальные условия указываются в виде уравнения при том же вызове.

Пример: численное решение дифференциального уравнения y'(x) = -2*y(x) + x при начальном условии y(0) = 1:

sol := dsolve({diff(y(x), x) = -2*y(x) + x, y(0) = 1}, y(x), numeric);

Команда возвращает процедурный объект, позволяющий получать значения решения в заданной точке. Для вычисления значения решения при x = 1.5 используйте:

sol(1.5);

Результат возвращается в виде списка вида [x = 1.5, y(x) = ...]. Чтобы построить график численного решения, используйте:

plots[odeplot](sol, [x, y(x)], 0 .. 5);

Если требуется решить систему уравнений, указывается множество уравнений и соответствующих начальных условий. Например, система:

{diff(y(x), x) = z(x), diff(z(x), x) = -y(x), y(0) = 1, z(0) = 0}

Решается так:

sol := dsolve({diff(y(x), x) = z(x), diff(z(x), x) = -y(x), y(0) = 1, z(0) = 0}, {y(x), z(x)}, numeric);

Для повышения точности расчётов можно использовать опции abserr и relerr, например:

dsolve(..., numeric, abserr = 1e-7, relerr = 1e-7);

Для получения списка всех доступных опций используйте справку Maple по команде ?dsolve,numeric.

Определение области интегрирования и шага расчета

При решении задачи Коши в Maple необходимо точно задать числовой интервал, на котором будет производиться численное интегрирование. Область интегрирования определяется начальной точкой $ x_0 $ и конечным значением $ x_k $, которое выбирается в зависимости от условий задачи и интересующего диапазона значений решения.

В Maple область интегрирования указывается явно при вызове численного метода, например, dsolve с параметром numeric. Пример:

dsolve({diff(y(x), x) = f(x, y), y(x0) = y0}, y(x), numeric, range = x0..xk);

Шаг расчета влияет на точность и скорость вычислений. В Maple шаг можно задать через опцию stepsize, например:

dsolve(..., stepsize = h);

Рекомендуется выбирать шаг h так, чтобы избежать накопления погрешностей. При высокой чувствительности решения – использовать более мелкий шаг, например, $ h = 0.01 $ или меньше. При стабильных уравнениях допустим шаг $ h = 0.1 $ или больше.

Контролировать реальный шаг можно через опции output = listprocedure или output = array для последующего анализа значений. Также важно учитывать автоматическую адаптацию шага в некоторых численных методах Maple, если не задан stepsize вручную.

Построение графика решения задачи Коши

После получения аналитического или численного решения задачи Коши в Maple, построение графика позволяет визуально оценить поведение решения на заданном интервале. Ниже приведены конкретные шаги для построения графика.

Убедитесь, что решение задачи сохранено в переменной. Например:
sol := dsolve({y'(x) = f(x, y), y(x0) = y0}, y(x), numeric);
Для численного решения используйте оператор plots[odeplot]. Пример построения графика:
plots[odeplot](sol, [x, y(x)], x = a..b);
Задайте точный интервал x = a..b в соответствии с областью определения решения.
При необходимости задайте параметры плотности точек, чтобы повысить точность отрисовки:
numpoints = 1000
Добавьте параметры оформления для наглядности:
color = red, thickness = 2, title = "График решения", labels = ["x", "y"]

Полный пример:


with(plots):
sol := dsolve({y'(x) = x*y, y(0) = 1}, y(x), numeric):
odeplot(sol, [x, y(x)], x = 0..5, numpoints = 1000, color = blue, thickness = 2, title = "Решение задачи Коши", labels = ["x", "y"]);

Если решение аналитическое, используйте plot с подстановкой:
plot(rhs(sol), x = a..b);
Для систем уравнений используйте списки переменных:
odeplot(sol, [[x, y1(x)], [x, y2(x)]], x = a..b);

Изучение графика позволяет определить области устойчивости, экстремумы, асимптотическое поведение и возможные особенности решения.

Анализ точности решения с помощью команды odeplot

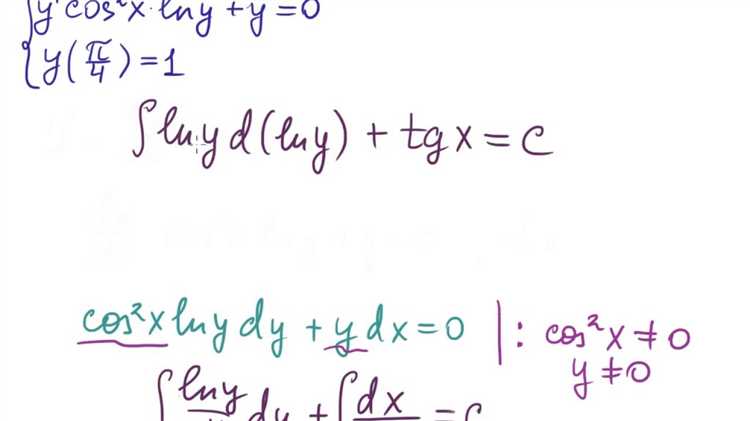
Команда odeplot из пакета plots позволяет визуально оценить точность численного решения задачи Коши, сравнивая графики при разных параметрах интегрирования.

Построение графиков решения при разных шагах метода:
- Используйте параметр stepsize для задания шага интегрирования.
- Сравните графики с крупным и мелким шагом – значительные отклонения укажут на недостаточную точность.
Оценка влияния метода интегрирования:
- В функции dsolve задайте разные численные методы (method=dverk, method=rkf45 и т.п.).
- Постройте графики с помощью odeplot для каждого варианта и выявите устойчивость решения.
Использование параметров точности:
- Установите abserr и relerr в dsolve для контроля абсолютной и относительной погрешностей.
- Сравните результаты с разными значениями параметров и визуализируйте изменения через odeplot.

Пример команд для анализа:

with(plots):
sol1 := dsolve({diff(y(t),t)=f(t,y(t)), y(0)=y0}, y(t), numeric, method=rkf45, stepsize=0.1):
sol2 := dsolve({diff(y(t),t)=f(t,y(t)), y(0)=y0}, y(t), numeric, method=rkf45, stepsize=0.01):
odeplot([sol1], [t, y(t)], 0..T, color=red), odeplot([sol2], [t, y(t)], 0..T, color=blue);

Красный график с крупным шагом и синий с мелким наглядно демонстрируют влияние шага интегрирования на точность.

Рекомендуется фиксировать параметры решения и проводить пошагенный сравнительный анализ с использованием odeplot, чтобы выявить оптимальные настройки численного метода и шаг интегрирования.

Сравнение численного и аналитического решений в Maple

В Maple аналитическое решение задачи Коши получают с помощью команды `dsolve` с опцией `explicit`, если уравнение допускает точное выражение. Численное решение строится функцией `dsolve` с параметром `numeric`. Для сравнения необходимо вычислить значения решений в одних и тех же точках по времени.

Пример: для уравнения y'(t) = -2y(t), y(0) = 1 аналитическое решение: y(t) = exp(-2t). Численное решение создаётся так: `sol := dsolve({diff(y(t), t) = -2*y(t), y(0)=1}, y, numeric)`. Далее получают массив значений, используя `y_val := [seq([t, rhs(sol(t))], t=0..2, 0.1)]`.

Чтобы оценить точность, вычисляют отклонения в точках: `abs(exp(-2*t) — rhs(sol(t)))`. Максимальная разница даёт представление о погрешности численного метода. При необходимости изменяют шаг интегрирования параметром `abserr` или `relerr` в `dsolve` для улучшения точности.

Визуальная проверка реализуется построением графиков обеих функций на одном поле командой `plots[display]`. Различия хорошо видны при большом шаге интегрирования или жёстких уравнениях, где численные методы требуют адаптации параметров.

При отсутствии аналитического решения сравнение сводится к проверке с разными параметрами численного метода и контролю сходимости решения. Maple позволяет использовать методы Рунге-Кутты разного порядка, что важно для выбора оптимального баланса между точностью и скоростью вычислений.

Вопрос-ответ:

Как задать задачу Коши в Maple для обычного дифференциального уравнения?

Для задания задачи Коши в Maple необходимо определить уравнение, переменные и начальные условия. Обычно используют команду `dsolve` с параметром `ic`, где указываются начальные значения функции и её производных в конкретной точке. Например, для уравнения y'(x) = y(x) с условием y(0)=1 запись будет выглядеть так: `dsolve({diff(y(x), x) = y(x), y(0) = 1}, y(x))`.

Можно ли в Maple решать задачи Коши для систем дифференциальных уравнений? Если да, то как?

Да, Maple позволяет решать задачи Коши для систем ОДУ. Нужно записать все уравнения системы и начальные условия для каждой из функций. Затем в команде `dsolve` передать множество уравнений и условий. Например: `dsolve({diff(x(t), t) = x(t) + y(t), diff(y(t), t) = -x(t) + y(t), x(0) = 1, y(0) = 0}, {x(t), y(t)})`. Maple выдаст общее или частное решение в зависимости от поставленной задачи.

Как проверить корректность решения задачи Коши, полученного в Maple?

После получения решения можно подставить его обратно в исходное уравнение и проверить, выполняются ли дифференциальные соотношения и начальные условия. В Maple для проверки можно использовать команду `simplify` и подставить решение в левую часть уравнения, затем сравнить с правой. Также удобно использовать `eval` для подстановки начальных значений, чтобы убедиться в соответствии. Если выражения сокращаются до тождества, решение правильное.

Какие есть ограничения при решении задачи Коши в Maple для сложных нелинейных уравнений?

Maple способен решать множество задач Коши как аналитически, так и численно, но для некоторых сложных или сильно нелинейных уравнений аналитическое решение может отсутствовать. В таких случаях рекомендуется использовать численные методы с командой `dsolve` и опцией `numeric`. Важно корректно задать начальные условия и параметры для численного решения, а также учитывать возможные особенности поведения решений, например, особые точки или устойчивость.