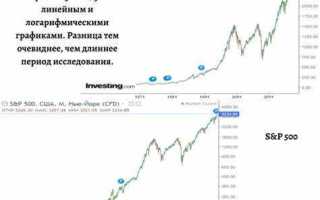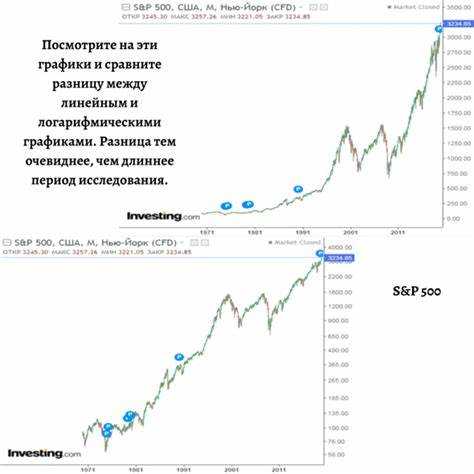
Визуализация данных с большими диапазонами значений требует использования логарифмической шкалы. В Mathematica реализация таких графиков осуществляется с помощью опций ScalingFunctions и LogPlot. Эти инструменты позволяют быстро перейти от линейного отображения к логарифмическому без необходимости вручную трансформировать данные.
Для одномерных функций логарифмический масштаб оси Y задаётся через LogPlot[f[x], {x, a, b}]. При необходимости масштабировать обе оси, используется опция ScalingFunctions → {«Log», «Log»} в функциях ListPlot, ListLinePlot и Plot. Это особенно полезно при анализе экспоненциальных трендов, степенных зависимостей или данных, охватывающих несколько порядков величин.
Если необходимо построить график с логарифмической осью X, но при этом оставить линейную шкалу по Y, применяется ScalingFunctions → {«Log», «Linear»}. При этом Mathematica корректно форматирует подписи осей, используя экспоненциальные обозначения, что облегчает восприятие графика. Для настройки отображения подписей и делений осей используются опции FrameTicks и TicksStyle.
При работе с логарифмическими осями важно исключить нулевые и отрицательные значения в данных, так как логарифм таких чисел не определён. Перед построением графика необходимо выполнить фильтрацию с помощью Select или DeleteCases, чтобы избежать предупреждений или ошибок визуализации.
Построение графика с логарифмической осью X
Для построения графика с логарифмической шкалой по оси X в Mathematica используйте опцию ScalingFunctions в функции Plot или аналогичных визуализаторах. Укажите значение {"Log", None}, чтобы применить логарифмическое масштабирование только по горизонтальной оси.
Пример: визуализация функции Log[x] на интервале от 1 до 1000:
Plot[Log[x], {x, 1, 1000}, ScalingFunctions -> {"Log", None}]Диапазон значений должен быть строго положительным. Если область определения функции включает ноль или отрицательные числа, Mathematica вернёт ошибку или пропустит соответствующие участки.
Для работы с дискретными точками используйте ListLogLinearPlot, если необходимо логарифмическое масштабирование только по X. Пример:
ListLogLinearPlot[{{1, 2}, {10, 3}, {100, 4}, {1000, 5}}]По умолчанию, логарифмическая ось отображает логарифмы по основанию 10. Для настройки подписей используйте Ticks с функцией LogScaleTicks из пакета PlotLegends`, либо настройте вручную:
Ticks -> {Table[{10^n, Superscript[10, n]}, {n, 0, 3}], Automatic}Если требуется наложение нескольких графиков, используйте Show и убедитесь, что все подграфики используют ScalingFunctions -> {"Log", None}.
Для логарифмической оси X с логарифмами по другому основанию примените преобразование вручную, например Log[2, x], и стройте график на обычной логарифмической шкале.
Построение графика с логарифмической осью Y
Для создания графика с логарифмической шкалой по оси Y в Mathematica используется опция ScalingFunctions → {«Log», None} в функции Plot или ListLogPlot, в зависимости от типа данных.
Пример построения аналитической функции с логарифмической осью Y:
Plot[Exp[x], {x, 0, 10}, ScalingFunctions → {"Log", None}]Если необходимо визуализировать набор дискретных точек, используйте ListPlot с соответствующей опцией:
ListPlot[Table[{x, Exp[x]}, {x, 0, 10}], ScalingFunctions → {"Log", None}]Важно: логарифмическая шкала не допускает нулевых или отрицательных значений. Убедитесь, что все значения по Y строго положительные. В противном случае Mathematica сгенерирует ошибку или пропустит такие точки без предупреждения.
Чтобы улучшить читаемость графика, рекомендуется задать явно интервал по оси Y с помощью опции PlotRange, например:
Plot[Exp[x], {x, 0, 10}, ScalingFunctions → {"Log", None}, PlotRange → {{0, 10}, {0.1, 10000}}]Для отображения вспомогательной сетки используйте GridLines → Automatic, что особенно полезно при логарифмическом масштабе:
Plot[Exp[x], {x, 0, 10}, ScalingFunctions → {"Log", None}, GridLines → Automatic]Если необходимо построить логарифмический график с использованием других функций визуализации (например, LogLogPlot или LogLinearPlot), предпочтительнее использовать именно ScalingFunctions, поскольку она предоставляет больший контроль над масштабами и их комбинациями.
Двумерный график с обеими логарифмическими осями
Для построения графика с логарифмическими масштабами по обеим осям в Mathematica используется параметр ScalingFunctions. Он принимает список из двух элементов, соответствующих масштабам по оси x и y. Указание "Log" задаёт логарифмическую шкалу.
Пример построения графика функции y = x^2 в двойном логарифмическом масштабе:
Plot[x^2, {x, 0.1, 10}, ScalingFunctions -> {"Log", "Log"}]Область определения по оси x должна быть положительной, поскольку логарифм от нуля и отрицательных чисел не определён. Если функция может принимать отрицательные значения по y, необходимо ограничить область или воспользоваться PlotRange:
Plot[Sin[x], {x, 0.1, 10}, ScalingFunctions -> {"Log", "Log"}, PlotRange -> {10^-2, 1}]График функции, определённой численно:
ListLogLogPlot[Table[{x, x^1.5 + RandomReal[0.5]}, {x, 1, 1000, 10}]]Для настройки подписей используется Frame -> True и FrameLabel:
Plot[x^3, {x, 0.01, 100}, ScalingFunctions -> {"Log", "Log"},
Frame -> True, FrameLabel -> {"x (log)", "y (log)"}]Чтобы уточнить деления и отрисовку осей, применяется Ticks. Для логарифмических делений удобно использовать функцию LogTicks из пакета PlotLegends` или задавать вручную:
Ticks -> {Table[{10^i, Superscript[10, i]}, {i, -2, 2}],
Table[{10^j, Superscript[10, j]}, {j, 0, 6}]}Использование функции LogPlot для построения логарифмических графиков
LogPlot используется для построения графиков функций с логарифмической шкалой по оси y. Это удобно при визуализации экспоненциального роста, степенных функций и данных, охватывающих несколько порядков величин.
- Синтаксис:
LogPlot[f[x], {x, xmin, xmax}]– строит график функцииf[x]на интервале[xmin, xmax]с логарифмической шкалой по оси y. - Форматы ввода:
f[x]может быть выражением любого типа, включая комбинации элементарных функций. Для множественных функций используйте список:LogPlot[{f1[x], f2[x]}, {x, a, b}]. - Ограничения: Функции
f[x]должны возвращать только положительные значения, иначеLogPlotне построит соответствующие участки. Для анализа поведения вблизи нуля используйтеPlotRange -> All.
Рекомендуемые параметры:
PlotRange -> All– для отображения всех допустимых значений.PlotStyle -> {Thick, Red}– для выделения кривой и улучшения читаемости.GridLines -> Automatic– для добавления вспомогательной сетки.PlotPoints -> 100– увеличивает плотность вычислений для более точного построения.WorkingPrecision -> 20– при необходимости высокой точности, особенно при малых значенияхx.
Пример:
LogPlot[Exp[x], {x, -2, 2}, PlotRange -> All, PlotStyle -> Blue, GridLines -> Automatic]Для логарифмической шкалы по обеим осям используйте комбинацию LogLogPlot (не встроенная функция, но доступна через пакеты или пользовательские реализации).
Для отображения асимптот и экстремумов используйте Epilog с Point и Line.
Настройка делений и подписей на логарифмических осях
Для точного контроля над делениями и подписями логарифмической шкалы в Mathematica используются параметры Ticks и ScalingFunctions. Ниже приведены рекомендации по их настройке для обоих осей.
- Логарифмическое масштабирование: установите
ScalingFunctions -> "Log"внутриPlot,ListLogPlotили других графических функций. Пример:Plot[10^x, {x, 0, 3}, ScalingFunctions -> {"Log", "Log"}]. - Автоматическая генерация делений: при использовании
ScalingFunctionsMathematica автоматически расставляет деления по логарифмической шкале (1, 10, 100 и т.д.). Однако эти значения можно переопределить вручную с помощьюTicks. - Задание пользовательских делений: определите список вручную, например:
Ticks -> {Table[{10^i, Superscript[10, i]}, {i, 0, 3}], Automatic}
Это создаст деления на оси X в точках 1, 10, 100, 1000 с подписями в виде степеней десяти. - Упрощение подписей: для кратких подписей используйте обычные числа:
{10^i, ToString[10^i]}вместо экспоненциальной записи. - Мелкие деления: добавьте их вручную, указав дополнительные позиции:
Join[Table[{10^i, Superscript[10, i]}, {i, 0, 3}], Table[{j, ""}, {j, 2, 9}*10^i, {i, 0, 2}]]
Это создаст основные деления с подписями и промежуточные – без. - Отключение подписей: для делений без текста укажите пустую строку:
{значение, ""}. - Форматирование подписей: примените функции, например
ScientificForm, черезStyleилиTextвнутриTicks.
Точные деления и подписи позволяют избегать визуального шума и обеспечивают читаемость при широких диапазонах данных. Настройку следует производить индивидуально под каждый график.
Преобразование обычного графика в логарифмический
Для перевода графика в логарифмический масштаб в Mathematica применяют опции ScalingFunctions и LogPlot или ListLogPlot в зависимости от исходных данных. При работе с функциями используется LogPlot[f[x], {x, xmin, xmax}], который автоматически строит график с логарифмической шкалой по оси Y.
Для данных в виде списка точек применяется ListLogPlot[data], где масштабирование происходит по оси Y. Если требуется логарифмическая шкала по оси X, используют опцию ScalingFunctions -> {"Log", "Linear"} в стандартной функции ListPlot:
ListPlot[data, ScalingFunctions -> {"Log", "Linear"}]
При необходимости логарифмического масштабирования обеих осей задают ScalingFunctions -> {"Log", "Log"}. Важно помнить, что логарифмическое масштабирование не допускает нулевых или отрицательных значений, поэтому данные следует предварительно фильтровать или смещать.
Для управления метками осей и их форматированием применяют опции Ticks с функциями генерации логарифмических делений, например, Ticks -> LogTicks (пользовательская функция), или используют встроенные шаблоны делений.
Оптимальным решением при сложном комбинировании масштабов и оформления является использование ScalingFunctions, позволяющей легко переключаться между линейным и логарифмическим режимом без перестроения данных. Это ускоряет эксперимент с визуализацией и сохраняет точность.
Построение логарифмического графика для набора экспериментальных данных
В Mathematica для построения логарифмического графика необходимо преобразовать оси с помощью параметров PlotRange и ScalingFunctions. При наличии набора данных, например, вида {{x1, y1}, {x2, y2}, …, {xn, yn}}, важно использовать функцию ListLogLogPlot для одновременного логарифмирования обеих осей. Если требуется логарифмировать только одну ось, используется ListPlot с опцией ScalingFunctions -> {«Log», «Linear»} или {«Linear», «Log»}.
Для корректного отображения данных на логарифмической оси все значения должны быть строго положительными. Перед построением рекомендуется фильтровать или корректировать нулевые и отрицательные значения, так как логарифм для них не определён.
Например, для набора данных experimentalData = {{0.1, 5}, {1, 50}, {10, 500}} команда ListLogLogPlot[experimentalData] построит график с логарифмическими осями X и Y.
При необходимости точной настройки диапазонов осей и меток применяется опция PlotRange, например, PlotRange -> {{0.01, 100}, {1, 1000}}. Для настройки делений осей рекомендуются функции Ticks, где можно задать пользовательские метки с использованием степеней десяти.
Для улучшения читаемости графика стоит учитывать толщину линий, размер маркеров и цвет, что задаётся опциями PlotStyle и PlotMarkers. Важным элементом является заголовок и подписи осей, которые задаются с помощью AxesLabel, содержащих описания в формате текста или с использованием формул Mathematica.
Экспорт логарифмического графика с сохранением масштаба
Для сохранения корректного логарифмического масштаба при экспорте графика из Mathematica важно использовать функции, поддерживающие векторные форматы, такие как PDF или SVG. При сохранении в растровых форматах (PNG, JPEG) возможна потеря четкости и масштабирования.
Перед экспортом убедитесь, что в графике явно задан параметр ScalingFunctions -> «Log». Это гарантирует правильное отображение осей в логарифмическом виде при последующем импорте или печати.
Рекомендуется использовать команду Export с указанием точного размера изображения через опцию ImageSize, чтобы избежать автоматического масштабирования, которое может исказить пропорции осей:
Export["graph.pdf", plot, ImageSize -> 600]
При необходимости интеграции графика в LaTeX или другие системы лучше выбирать PDF с векторной графикой. Это обеспечивает масштабируемость без потери качества и сохраняет правильные метки осей.
Если требуется экспорт в растровый формат, применяйте высокое разрешение, например:
Export["graph.png", plot, ImageResolution -> 300]
Это минимизирует размытость при увеличении, однако масштаб осей останется фиксированным визуально без возможности интерактивного изменения.
Вопрос-ответ:
Как в Mathematica построить график с логарифмической шкалой по оси Y?
Для построения графика с логарифмической шкалой по оси Y в Mathematica нужно воспользоваться опцией ScalingFunctions -> «Log» в функции Plot или ListPlot. Например, Plot[Sin[x], {x, 1, 10}, ScalingFunctions -> {«Linear», «Log»}] построит график с линейной шкалой по оси X и логарифмической по оси Y. Эта настройка позволяет отобразить данные с большим диапазоном значений удобнее.
Какие типы логарифмических шкал поддерживаются в Mathematica и как их задать?
Mathematica поддерживает несколько вариантов логарифмических шкал: с основанием 10 («Log10»), с натуральным основанием («Log»), а также произвольные основание можно задать через функцию ScalingFunctions, указав пользовательскую трансформацию. Например, ScalingFunctions -> {«Log», «Exp»} задаёт логарифмическое преобразование по оси Y и обратное — экспоненциальное. Для обычного десятичного логарифма используется «Log10». При необходимости можно реализовать собственную функцию преобразования.
Как влияет использование логарифмического масштаба на интерпретацию графиков с экспоненциальным ростом данных?
При отображении данных с экспоненциальным ростом на линейной шкале кривая быстро уходит вверх, что затрудняет анализ. Логарифмический масштаб преобразует экспоненту в линейную зависимость, позволяя лучше увидеть тренды и сравнить скорость роста. Это помогает определить закономерности и выявить отклонения от ожидаемой экспоненциальной динамики, так как прямые линии на логарифмическом графике отражают постоянную скорость роста.
Какие могут возникнуть проблемы при использовании логарифмических шкал в Mathematica и как их избежать?
Основная сложность при работе с логарифмическими шкалами — необходимость положительных значений данных, так как логарифм от нуля или отрицательных чисел не определён. Если данные содержат нули или отрицательные значения, Mathematica может выдавать ошибки или пустые участки графика. Чтобы избежать этого, следует предварительно фильтровать данные, заменять нули малыми положительными числами или использовать альтернативные методы визуализации. Также стоит контролировать подписи осей и отметки, чтобы они корректно отражали логарифмическое преобразование.