Как сделать периодическую функцию в mathcad

Периодические функции – ключевой инструмент при моделировании процессов, повторяющихся во времени. В Mathcad можно реализовать такие функции несколькими способами, включая явное задание по формуле, использование встроенных операторов и построение через условные выражения. Оптимальный выбор зависит от задачи и требований к точности и скорости вычислений.

Для создания простой периодической функции, такой как пилообразный или прямоугольный сигнал, эффективно использовать оператор mod. Например, выражение mod(t, T) позволяет задать поведение, повторяющееся с периодом T. Это особенно полезно при необходимости синтеза сигналов в инженерных расчётах или задачах цифровой обработки данных.

Более сложные формы, включая комбинации синусоидальных сигналов с фазовыми сдвигами, удобно реализуются через параметризацию. Mathcad поддерживает векторные и матричные операции, что позволяет построить одну периодическую функцию на основе базовых гармоник и управлять их амплитудами и частотами в режиме реального времени.

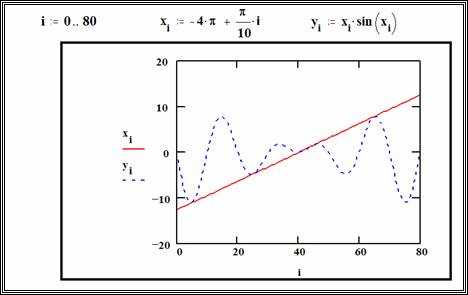
Если требуется периодическая функция с определённым поведением на каждом интервале, целесообразно использовать оператор if в сочетании с функцией floor. Это позволяет вручную определить форму сигнала внутри одного периода и повторить её через сдвиг по оси времени. Такой подход применим для моделирования пользовательских импульсных форм и нестандартных профилей нагрузок.

Определение функции с использованием оператора модуло

Оператор mod в Mathcad позволяет задать периодическую зависимость за счёт выделения остатка от деления. Это особенно полезно при создании функций, повторяющих своё поведение через фиксированный интервал.

• Синтаксис: mod(x, T), где x – аргумент функции, T – период.
• Пример: для создания функции, повторяющейся каждые 3 единицы, используйте mod(x, 3).
• Встроенные функции можно использовать совместно с mod. Пример: f(x) := sin(mod(x, 2·π)) создаёт периодическую синусоиду с периодом 2π.
• Для произвольной формы сигнала: f(x) := piecewise(mod(x, T) < a, y1, mod(x, T) < b, y2, y3).

Рекомендации по применению:

1. Избегайте прямого сравнения значений mod(x, T) с точками разрыва из-за численных погрешностей. Лучше использовать интервалы.
2. Для симметричных функций предпочтительно использовать mod(x + T/2, T) - T/2, чтобы получить ось симметрии в центре периода.
3. Визуализируйте результат после определения, чтобы убедиться в корректной периодичности.

Оператор mod особенно эффективен при моделировании пилообразных, прямоугольных и триангулярных сигналов. Его применение позволяет упростить описание функции и обеспечить точную повторяемость формы.

Построение периодической функции на основе условных выражений

Для создания периодической функции в Mathcad можно использовать операторы условного ветвления. Это позволяет вручную определить поведение функции на каждом интервале периода, обеспечивая гибкость и точность моделирования.

Рассмотрим пример построения функции f(t), периодической с периодом T = 2. Пусть на интервале [0, 1) функция принимает значение sin(π·t), а на интервале [1, 2) – значение 0. Тогда формула с применением условных выражений выглядит следующим образом:

f(t) := if mod(t, 2) < 1 then sin(π·mod(t, 2)) else 0

Оператор mod(t, 2) возвращает значение аргумента в пределах одного периода [0, 2). Это позволяет повторно использовать определение функции на базовом интервале для всех последующих циклов. Mathcad автоматически интерпретирует логические условия, возвращая соответствующее значение функции в зависимости от результата проверки.

Для построения графика введите диапазон значений переменной: t := 0, 0.01 .. 10. Затем задайте f(t) как функцию от этого диапазона и постройте график. Функция будет отображаться как чередование сегментов синуса и нулевого уровня, строго по заданным правилам.

Избегайте использования вложенных if при большом числе участков – вместо этого разбейте определение на вспомогательные функции или примените оператор piecewise (в версиях Mathcad Prime). Это улучшит читаемость и упрощает отладку.

Использование встроенной функции sawtooth для создания пилы

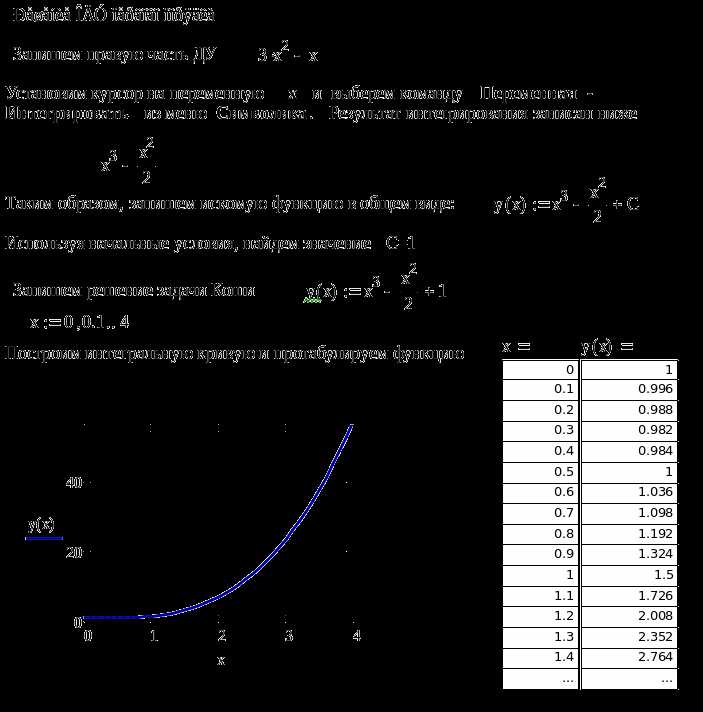
В Mathcad функция sawtooth(t) позволяет сформировать периодическую линейно возрастающую функцию с последующим мгновенным спадом до начального значения. Это типичная форма сигнала «пила». Функция принимает один аргумент – t, представляющий независимую переменную, как правило, время.

Для управления параметрами пилы необходимо масштабировать аргумент и результат функции. Например, для получения пилы с амплитудой A и периодом T используется выражение:

f(t) := A · sawtooth(2·π·t/T)

Аргумент 2·π·t/T обеспечивает корректное преобразование времени в фазовый угол. Без этого преобразования результат будет не соответствовать ожидаемому периоду. Множитель A масштабирует амплитуду от стандартного диапазона [-1, 1] к желаемому [0, A], если применить дополнительное преобразование:

f(t) := A·(sawtooth(2·π·t/T) + 1)/2

При моделировании систем, чувствительных к фазовому сдвигу, можно добавить фазовую задержку φ:

f(t) := A·(sawtooth(2·π·(t — φ)/T) + 1)/2

Функция sawtooth работает эффективно при векторизованных расчетах. Для генерации массива значений на интервале времени:

t := 0, Δt .. T_max

f(t) автоматически создаст вектор значений пилы по указанным параметрам.

Визуализация графика через Insert → Graph → X-Y Plot позволяет мгновенно проверить корректность настроек. Подбор Δt критичен для адекватного отображения формы сигнала – рекомендуется устанавливать не менее 100 точек на период.

Формирование синусоидального сигнала с заданным периодом

В Mathcad синусоидальный сигнал с периодом T формируется через функцию синуса с аргументом, масштабированным по времени. Ключевая формула:

y(t) := A·sin(2·π·t/T + φ)

• A – амплитуда сигнала;
• T – период в секундах;
• φ – начальная фаза в радианах;
• t – переменная времени (вектор).

Для корректной дискретизации сигнала необходимо задать временной вектор с шагом Δt, удовлетворяющим условию Найквиста: Δt ≤ T / 20. Пример:

t := 0, Δt .. N·T

Рекомендуемые действия:

1. Определить T в секундах (например, T := 0.01).
2. Выбрать A (например, A := 5).
3. Задать φ, при необходимости (например, φ := π/4).
4. Установить Δt, кратное T/20 (например, Δt := T/50).
5. Сформировать временной вектор t (например, t := 0, Δt .. 0.1).
6. Определить функцию y(t) по приведённой формуле.

Для отображения графика используйте встроенную панель графика (Insert → Graph → X-Y Plot). По оси X – t, по оси Y – y(t).

При необходимости изменения частоты сигнала используйте соотношение f = 1/T и пересчитывайте T соответствующим образом. Например, для f = 50 Гц → T := 1/50.

Комбинирование нескольких периодических компонентов в одну функцию

В Mathcad объединение нескольких периодических функций реализуется через простое суммирование или умножение исходных компонент. Основная задача – корректное определение параметров каждой функции: амплитуды, частоты, фазы и смещения по оси времени.

Для сложения периодических сигналов с разными периодами рекомендуется использовать выражение вида:

f(t) = A₁·sin(2π·f₁·t + φ₁) + A₂·cos(2π·f₂·t + φ₂) + …

Здесь A – амплитуда, f – частота, φ – начальная фаза. В Mathcad удобно определить каждую функцию отдельно, а затем задать итоговую как сумму этих функций, что обеспечивает прозрачность и удобство редактирования.

Если периоды компонентов не совпадают, итоговая функция будет сложным периодическим или даже квазипериодическим сигналом. В таких случаях полезно выбирать общий период как НОК (наименьшее общее кратное) периодов всех компонент, если это возможно.

При необходимости выделения гармонических составляющих рекомендуется использовать функции Fourier в Mathcad, что позволяет анализировать и корректировать спектр итоговой функции.

Важный аспект – единообразие размерностей и единиц времени. Несоблюдение этого приводит к искажению результата и неправильной визуализации графиков.

Визуализация и проверка периодичности на графике

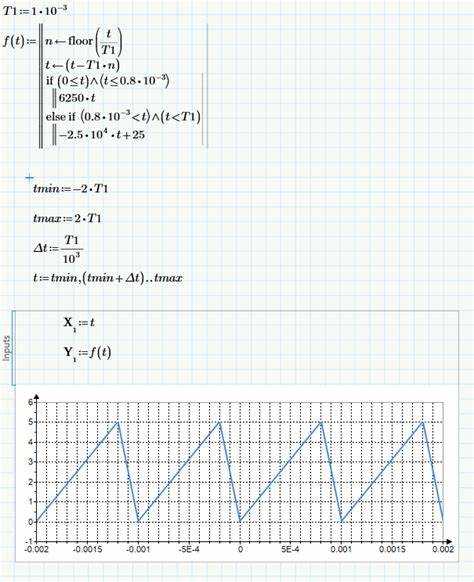
Для подтверждения периодичности функции в Mathcad требуется построить график с несколькими циклами. Используйте масштаб по оси X, покрывающий минимум три периода, чтобы визуально убедиться в повторении формы сигнала.

При построении графика задайте точность вычислений, уменьшая шаг дискретизации. Например, если период T=2π, оптимальным будет шаг порядка 0.01 для гладкой кривой. Слишком крупный шаг может скрыть детали повторения.

Рекомендуется отобразить несколько периодов функции на одном графике. Это позволит выявить аномалии и отклонения, например, дрейф амплитуды или сдвиг по фазе, которые нарушают идеальную периодичность.

Для более точной проверки периодичности вычислите разницу значений функции через интервал T, сравнив f(x) и f(x+T) для набора точек. Постройте график разности, который должен стремиться к нулю во всех точках, если периодичность соблюдена.

Используйте функции Mathcad для наложения нескольких графиков: исходной функции и её сдвига по оси X на период T. Совпадение кривых визуально подтверждает корректность реализации периодической функции.

Вопрос-ответ:

Как задать периодическую функцию в Mathcad с помощью стандартных инструментов?

В Mathcad для создания периодической функции можно использовать оператор остатка от деления (mod). Например, если нужно задать функцию с периодом T, то в аргументе функции используют выражение вида mod(x, T), где x — переменная. Таким образом, функция «сбрасывается» к начальному значению при достижении периода, обеспечивая повторение значений с нужной регулярностью. Также можно применять встроенные тригонометрические функции, которые по своей природе периодичны, либо комбинировать их с оператором mod для получения более сложных периодических форм.

Можно ли в Mathcad создавать периодические функции с переменным периодом?

Да, в Mathcad возможно реализовать периодические функции с периодом, меняющимся в зависимости от параметров. Для этого в формуле периода вместо константы используют переменную или выражение, зависящее от других параметров. Однако стоит учитывать, что такие функции могут иметь нестандартное поведение и потребуют более тщательной настройки. Для контроля изменения периода удобно использовать условные операторы или вспомогательные переменные, что поможет адаптировать функцию под разные сценарии.

Какие типичные ошибки возникают при построении периодических функций в Mathcad и как их избежать?

Частой ошибкой является неправильное использование оператора mod, например, если забыть учесть сдвиг или начальное значение, функция может смещаться и не соответствовать ожидаемому виду. Также иногда неправильно задают диапазон аргумента, что приводит к неверной визуализации графика. Чтобы избежать проблем, стоит внимательно проверять параметры периода, использовать контрольные значения для проверки поведения функции, а также по возможности строить графики с небольшими интервалами для точной оценки результата.

Как визуально проверить корректность заданной периодической функции в Mathcad?

Для проверки функции достаточно построить её график в Mathcad на нескольких периодах. Это позволит увидеть повторяемость значений и убедиться в правильности настройки периода. Также можно вычислить значения функции в точках, соответствующих границам периодов, чтобы удостовериться, что функция возвращается к исходному значению. Если функция задана корректно, график будет повторяться с одинаковой формой и амплитудой через равные промежутки по оси аргумента.

Можно ли комбинировать разные типы периодических функций в Mathcad для получения сложных сигналов?

Да, Mathcad позволяет создавать сложные периодические функции, комбинируя несколько простых. Например, можно суммировать синусоиды с разными частотами и амплитудами для моделирования сложных волн. При этом важно правильно задать периоды и фазовые сдвиги для каждой составляющей, чтобы получить нужный итоговый сигнал. Такая возможность особенно полезна при изучении сигналов с несколькими гармониками или при моделировании сложных физических процессов.